Уравнения движения

В этом разделе рассматриваются только наиболее распространенные формы дифференциальных уравнений движения идеальной жидкости, а именно — уравнения в форме Л. Эйлера и в форме И. Громеки, а также их интегралы.

Для вывода дифференциальных уравнений движения в потоке выделяется жидкий объем и рассматриваются силы, которые на него действуют. Жидким называется объем, контуры которого движутся вместе с жидкостью, т.е. этот объем состоит из одних и тех же частиц жидкости. На рис.5 такой объем взят в виде прямоугольного параллелепипеда АВСDЕFLК со сторонами Δ х, Δ y, Δ z.

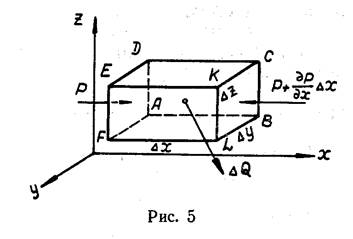
На жидкость, заключенную в объеме АВСDЕFLК, действуют поверхностные силы — силы давления на грани объема и массовые силы (например, силы тяжести). Поверхностных касательных сил нет, так как рассматривается идеальная жидкость.

Согласно второму закону Ньютона, сумма всех внешних сил, действующих на жидкость, равна ее массе, умноженной на ускорение. В проекциях на координатные оси это можно записать в следующем виде (в проекции на ось х):

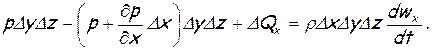
Раскрыв скобки, заменив проекции массовых сил , , 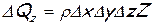где Х, Y, Z — проекции ускорений от массовых сил, и поделив обе части равенства на массу , получим

Уравнения в проекциях на две другие координатные оси запишутся аналогично. Окончательно имеем:

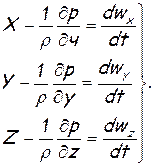(1.27)

Эти уравнения были получены Леонардом Эйлером в 1755 году и носят его имя. Они справедливы как для несжимаемой, так и для сжимаемой жидкости.

При выводе уравнений движения реальной жидкости необходимо в число действующих сил включить еще силы трения. Система уравнений будет напоминать систему Эйлера, но левые части равенств будут дополнены добавочными слагаемыми, учитывающими трение [1].

Другая форма дифференциальных уравнений движения идеальной жидкости была предложена профессором Казанского университета И.С.Громекой в 1881 году. Уравнения Громеки легко могут быть получены из уравнений Эйлера. Принимая во внимание, что w=w(x,y,z,t), ускорение, входящее в правую часть первого уравнения системы (1.27), можно записать следующим образом:

или, так как то

(1.28)

(два последних уравнения записаны по аналогии). Первые слагаемые в правых частях системы (1.28) представляют собой местное ускорение, т.е. изменение скорости по времени в данной точке пространства. Остальные слагаемые определяют конвективное ускорение, т.е. изменение скорости по времени (связанное с перемещением частицы жидкости из одной точки пространства в другую. Если, например, жидкость находится в установившемся движении, то местное ускорение равно нулю, так как в каждой точке пространства скорость по времени не изменяется. Что касается конвективного ускорения, то оно в этом случае может быть отличным от нуля, если при перемещении жидкости в пространстве ее скорость изменяется.

Преобразования Громеки состоят в следующем. Прибавляя и вычитая из правой части первого уравнения (1.28) величину

получим

или, принимая во внимание формулы (1.6),

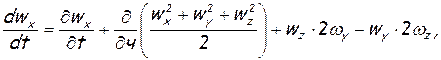
или

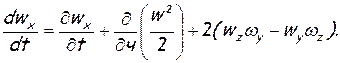
Аналогичные преобразования можно сделать и для двух других уравнений (1.28). Тогда, после подстановки значений ускорений в систему уравнений Эйлера (1. 27), последняя приобретает вид:

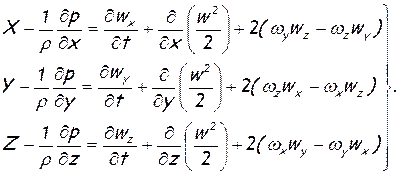(1.29)

Это есть уравнения Громеки. Удобство их заключается в том, что они содержат величины, определяющие в явном виде поступательное и вращательное движение.

В Англии аналогичные уравнения были получены несколько позднее Лэмбом.

Интегрирование уравнений движения наиболее удобно вести, используя систему уравнений в форме Громеки (1.29). Рассмотрим интегралы уравнений движения только для случая несжимаемой жидкости.

В большинстве случаев в качестве массовых сил, действующих в жидкости, фигурируют силы тяжести. Эти силы имеют потенциал. Это значит, что существует такая функция, называемая силовой функцией U, частные производные от которой по х, у и z равны соответствующим проекциям ускорений от массовых сил 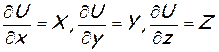. Тогда при ρ=const первое уравнение системы (1.29) можно записать так:

Следовательно, вместо системы (1.29), можно записать такую:

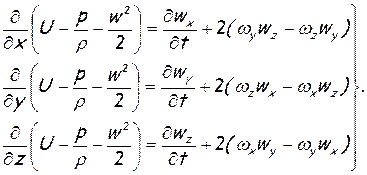(1.30)

В общем случае система уравнений (1.30) не интегрируется, поэтому рассмотрим частные случаи.

Неустановившееся безвихревое движение несжимаемой жидкости ω _x= ω _y = ω _z = 0

Если умножить уравнения (1.30) соответственно на dх, dу и dz и сложить, то получится

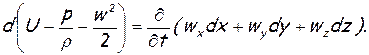
При ω _x= ω _y = ω _z = 0, как это следует из формул (1.6), получается

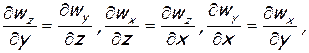
а это значит, что величина, стоящая в скобках в правой части последнего уравнения, является полным дифференциалом некоторой функции φ[2], следовательно,

тогда

(1.31)

Интегрирование дифференциального уравнения (1.31) дает

(1.32)

где F(t) - произвольная функция времени. Она определяется из начальных условий. Выражение (1.32) называется интегралом Лагранжа.

Установившееся движение несжимаемой жидкости

Умножив уравнения системы (1.30) при указанных условиях на dх, dу и dz и сложив их, получим

(1.33)

Уравнение (1.33) легко интегрируется, когда определитель равен нулю. Тогда получается следующее выражение:

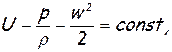(1.34)

которое называется интегралом Бернулли.

Рассмотрим, при каких условиях определитель обращается в нуль.

1. Если ω _x= ω _y =ω _z = 0, т.е. вторая строка состоит из нулей, то определитель равен нулю. Это безвихревое движение жидкости. Постоянная в уравнении Бернулли (1.34) в этом случае имеет одно и то же значение для всего потока.

2. Если т.е. члены первой строки пропорциональны членам третьей строки, то определитель равен нулю. Записанное условие представляет собой уравнение линий тока [3]. Таким образом, в данном случае уравнение Бернулли справедливо для линии тока. Следовательно, в случае вихревого движения константа в уравнении (1.34) сохраняет свое значение вдоль линии тока, а при переходе от одной линии тока к другой — меняется.

3. Если то определитель также равен нулю. Это условие представляет собой условие параллельности линии, проведенной в жидкости, вектору угловой скоростиω, т.е. является уравнением вихревых линий. Следовательно, константа в уравнении (1.34) сохраняет свое значение не только вдоль линии тока, но и вдоль вихревой линии.

4. Определитель равен нулю и при 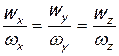. Это условие параллельности векторов линейной и угловой скорости: частицы жидкости движутся в этом случае поступательно, одновременно вращаясь в плоскости, перпендикулярной поступательному движению, подобно тому, как перемещается винт или штопор. Впервые на этот случай указал И.С. Громека.

Подводя итог, можно сказать, что интеграл Бернулли в случае безвихревого течения справедлив для всего потока, а в случае вихревого — только для линии тока или для вихревой линии.

Вновь обращаясь к уравнению (1.34), запишем его в том виде, в котором оно обычно применяется для практических целей. В большинстве случаев массовыми силами, действующими в жидкости, являются силы тяжести. Если ось z направить вертикально вверх, то проекции ускорений от массовых сил запишутся так: X=0, Y=0, Z= –g, где g — ускорение силы тяжести. Подставив это в (1.34), имея в виду, что U= –gz, получим

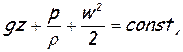(1.35)

или

(1.36)

Формулы (1.35) и (1.36) представляют разные варианты известного уравнения Даниила Бернулли для идеальной несжимаемой жидкости.

[1] Вывод этих уравнений см. в файле Уравнение движения вязкой жидкости.pdf

[2] Функция φ называется потенциалом скорости.

[3] Напомним, что уравнение линий тока получается как условие параллельности линии тока вектору скорости в данной точке, т.е. проекции отрезка линии тока dх, dу и dz должны быть пропорциональны компонентам вектора скорости w_x, w_y, и w_z.

Дата добавления: 2015-05-10