Метод Гаусса

Метод Гаусса, або метод послідовного виключення невідомих має декілька модифікацій. Розглянемо схему єдиного ділення, за якою систему розв’язують в два етапи. На першому етапі вихідну систему рівнянь зводять до рівносильної їй системи трикутної форми. Цей процес перетворень називають прямим ходом. На другому етапі, який називають зворотнім ходом, знаходять розв’язок системи лінійних рівнянь трикутної форми за допомогою підстановки відомих розв’язків. Оскільки перетворення системи є фактично перетвореннями коефіцієнтів при невідомих і вільних членів, то перетворення проводять над розширеною матрицею системи.

В процесі розв’язання системи рівнянь потрібно організувати контроль правильності ходу обчислень. Підсумковий контроль легко провести, підставивши одержані корені в систему рівнянь.

Щоб вчасно виявити (і виправити) можливі випадкові обчислювальні помилки, доцільно забезпечити контроль правильності обчислень на кожному проміжному етапі обчислень. Для цього до обчислювальної схеми вводять два додаткових стовпчики: контрольну суму і рядкову суму.

Спочатку цим сумам присвоюють одні і ті ж значення – суми елементів рядків розширеної матриці системи рівнянь. В ході перетворень над елементами контрольної суми виконують такі самі дії, що й над відповідними елементами рядка матриці, а в стовпець рядкових сум записують суми елементів новоутворених рядків розширеної матриці. Якщо відповідні рядкові і контрольні суми практично збігаються (можливі розбіжності із-за похибок арифметичних операцій), то обчислення проведено правильно. В противному випадку, потрібно шукати помилку в обчисленні того рядка, де суми не співпадають. Зауважимо, що похибки арифметичних операцій можуть бути великими, якщо ділення проводилось над числами близькими до нуля. В цьому випадку говорять, що має місце нестійкість алгоритму і таку систему лінійних рівнянь потрібно розв’язувати іншим методом.

Зазначений спосіб організації контролю за ходом обчислення по суті означає одночасне розв’язування двох систем лінійних рівнянь з однаковою головною матрицею, але з різними вільними членами (в другій системі вільними членами є рядкові суми). Якщо правильно проведено обчислення коренів, то розв’язки другої системи повинні на одиницю перевищувати відповідні корені першої системи.

«Ітераційні методи розв’язування систем лінійних рівнянь»

Застосування методу Гаусса для розв’язання системи лінійний рівнянь з великою кількістю невідомих досить громістке. В цих випадках краще використовувати ітераційні методи, тобто методи, які дозволяють будувати послідовність наближень, границя якої буде розв’язком системи лінійних рівнянь. Безумовно, що ця система повинна мати один, єдиний розв’язок.

Спочатку потрібно систему лінійних рівнянь подати у вигляді:

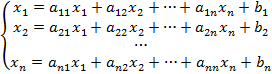(1)

Якщо виконується хоча б одна із умов , , 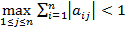, то система рівнянь (1) має єдиний розв’язок, який є границею послідовності, що одержується методом простої ітерації або методом Зейделя.

Зауважимо, що систему n лінійних рівнянь з n невідомими, записану в традиційній звичній для нас формі, завжди можна подати у вигляді (1), причому так, щоб виконувалися умови збіжності. Наприклад, якщо модуль кожного діагонального елемента матриці системи більший від суми модулів інших елементів рядка, тобто

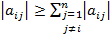, i =1,2,…, n (2)

то, розв’язавши перше рівняння відносно х ₁, друге – відносно х ₂ і т.д., дістанемо систему:

, (i =1, 2,..., n), де 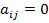, 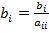. При цьому буде виконуватися перша умова збіжності. Якщо ж система така, що умова (2) не виконується, то за допомогою елементарних перетворень системи можна домогтися її виконання.

Для розв’язання системи рівнянь методом простої ітерації за початкове наближення можна брати довільні значення коренів, наприклад, підставляти значення вільних членів (х1 = b ₁, х ₂= b ₂,..., х_n = b_n). Підставляючи їх в праві частини системи (1), ми одержимо нові значення невідомих. Знову підставляємо одержані корені в праві частини системи (1), одержуючи нові значення невідомих і т.д. Цей процес продовжують до тих пір, поки не досягнуть бажаної точності.

Метод Зейделя відрізняється від методу простої ітерації тільки тим, що при обчисленні х_і на k -му кроці враховуються значення х ₁, х ₂,..., х_{k –1}, обчислені не на попередньому а на цьому самому кроці. Завдяки тому, що значення цих коренів одержуються в якійсь мірі уточненими, метод Зейделя має кращу збіжність в порівнянні з методом простої ітерації.

«Інтерполяційний поліном Лагранжа»

Дата добавления: 2015-05-10