Множители. Многочлены. Разложение многочлена на

Многочлены. Разложение многочлена на

Многочленом (или полиномом) 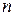-ой степени от неизвестного 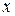называют выражение

, (1.12)

Коэффициенты многочлена (1.12) произвольные действительные или комплексные числа, причем старший коэффициент .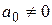

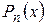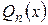Два многочлена и считаются равными в том случае, если равны их коэффициенты при одинаковых степенях неизвестной.

Помимо многочленов первой степени, квадратных, кубических и т.д., многочленом нулевой степени считают действительные или комплексные числа, отличные от нуля. число нуль считается многочленом, степень которого неопределена.

На множестве многочленов 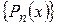определены операции сложения, умножения, которые удовлетворяют свойствам коммутативности, ассоциативности и дистрибутивности.

Для умножения многочленов обратная операция – деление – не существует.

Для любых двух многочленов, которые обозначим как целые функции 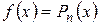, , 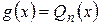можно найти такие многочлены 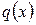и , что

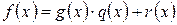. (1.13)

Это вытекает из алгоритма деления с остатком. Многочлен 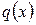называется частным от деления 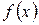на , а -остатком от деления.

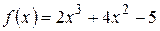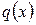Пример 1.6. Для и . Найти и .

Деля 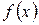на , получим

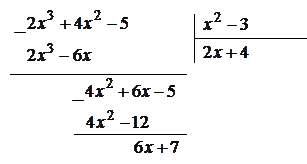Следовательно, 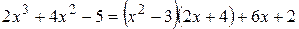, где , .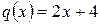

Если 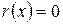, то 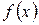делится на . Многочлены и 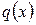будут делителями этого многочлена. Если у многочленов 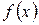и нет общих делителей, то они взаимно простые.

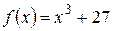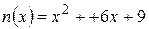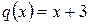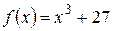Пример 1.7. а) и имеет общий делитель . б) и 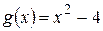взаимно простые.

Если 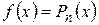, а 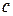- некоторое число, то число , полученное заменой числом 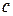, называется значением многочлена 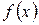при 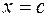. Если 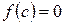, то 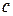называется корнем многочлена.

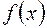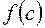Теорема Безу. Остаток от деления многочлена на линейный многочлен равен значению многочлена 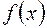при .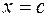

Следствие. Число 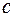тогда и только тогда будет корнем многочлена 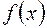, если 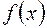делится на .

Может оказаться, что многочлен 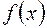делится не только на , но и на более высокие его степени, т.е.

(1.14)

где многочлен 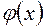уже не делится на . Число 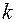называется кратностью корня 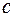, сам корень 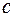- -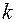кратным корнем многочлена 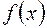. Если 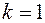, то говорят, что корень 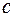-простой.

Пример 1.8. а) Для 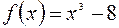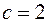простой корень.

б) Для 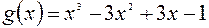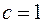- трехкратный корень.

Известно, что существует многочлены с действительными коэффициентами, не имеющие действительных корней: 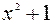-один из таких многочленов. На множестве комплексных чисел справедлива основная теорема алгебры комплексных чисел.

Теорема. Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.

Из основной теоремы следует, что после конечного числа шагов мы придем к разложению многочлена 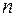-ой степени 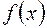в произведение 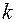линейных множителей.

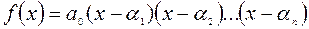(1.15)

где 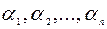- действительные или комплексные корни.

Разложение (1.15) является для многочлена 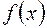единственным с точностью до порядка сомножителей разложением такого типа.

Пример 1.9. Разложить на множители многочлен 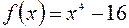. Имеем .

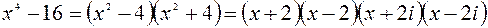Всякий многочлен 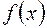степени 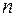, , 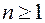с любыми числовыми коэффициентами имеет 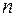корней, если каждый из корней считать столько раз, какова его краткость.

Формула Виета. Пусть в разложении (1.15) многочлена 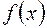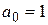, тогда

.

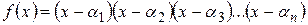Перемножая скобки, приведя подобные члены и сравнивая полученные коэффициенты с коэффициентами из (1.15), мы получим равенства, называемые формулами Виета, которые выражают коэффициенты многочлена через его корни:

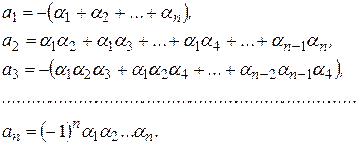(1.16)

При 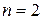эти формулы превращаются в известную из школьной алгебры связь между корнями и коэффициентами квадратного многочлена (уравнения).

Пример 1.10. Составить многочлен 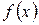третьей степени, имеющий простые корни 1, 2 и 3.

По формулам Виета получим:

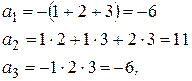
поэтому

Если 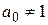, то для применения формулы (1.16) необходимо сначала разделить все коэффициенты на , что не влияет на корни многочлена. В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему.

Пусть у многочлена (1.12) все коэффициенты действительные числа и имеется комплексный корень 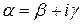, т.е.

Известно, что последнее равенство не нарушится, ели в нем все числа заменены на сопряженные, при этом все коэффициенты останутся без изменения, т.е .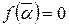

Если комплексное число 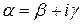служит корнем многочлена 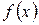с действительными коэффициентами, то корнем для 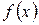будет и сопряженное число 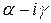. Следовательно, многочлен 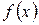будет делиться на квадратный трехчлен

, (1.17)

коэффициенты которого действительные числа.

Таким образом, комплексные корни всякого многочлена с действительными коэффициентами попарно сопряжены.

Всякий многочлен 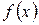с действительными коэффициентами представим, притом единственным способом (с точностью до порядков множителей), в виде произведения своего старшего коэффициента и нескольких многочленов с действительными коэффициентами, линейных вида 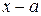, соответствующих его действительным корням, и квадратных вида 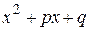, где 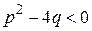, соответствующих парам сопряженных комплексных корней.

Пример 1.11.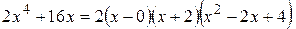

№1.9. Найдите сумму коэффициентов многочлена

№1.10. Делится ли многочлен 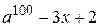на ?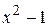

№1.11. Найдите остаток от деления многочлена 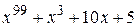на многочлен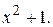

№1.12. Остатки от деления многочлена 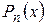на и 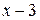равны соответственно 5 и 7. Найдите остаток от деления этого многочлена на .

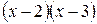№1.13. Найдите 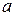и 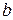, если известно, что многочлен 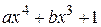делится на .

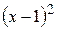Дата добавления: 2015-05-26