
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Жесткие уравнения
|
|
|
|
Пример, приведенный в предыдущем разделе, доказывает, что неустойчивость может происходить при сколь угодно малом h в случае устойчивого, но не строго устойчивого метода. Однако, даже строго устойчивые методы могут вести себя неустойчиво, если h слишком велико. Такая ситуация возникает при решении дифференциальных уравнений, которые называют жесткими.
Рассмотрим уравнение
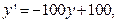 y(0)=
y(0)=  . (13.1)
. (13.1)
Данное уравнение можно записать в виде  , здесь
, здесь 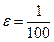 – малый параметр.
– малый параметр.
Таким образом, рассмотренная нами ситуация имеет место в уравнениях с малым параметром при старшей производной.
Точным решением этой задачи является функция
y(x)=( -1)
-1)  +1. (13.2)
+1. (13.2)
Проведем исследование этого решения на устойчивость относительно возмущения начальных данных. Возмутим начальное условие на бесконечно малую величину  . Получим задачу
. Получим задачу 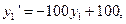
 . Ее решение имеет вид
. Ее решение имеет вид 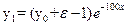 . Вычислим разность
. Вычислим разность 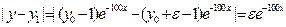 .
.
Экспоненты при больших значениях х убывают, следовательно, решение устойчиво! Действительно, если мы заменим начальное условие на 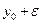 , то решение изменится на
, то решение изменится на 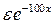 . Малому изменению начального условия соответствует малое изменение решения. Решение устойчиво. Метод Эйлера в применении к задаче (22.1) принимает вид
. Малому изменению начального условия соответствует малое изменение решения. Решение устойчиво. Метод Эйлера в применении к задаче (22.1) принимает вид
 , (13.3)
, (13.3)
и точное решение этого разностного уравнения первого порядка выражается формулой
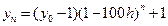 . (13.4)
. (13.4)
Это решение можно получить двумя способами.
1. Поскольку известно точное решение, то можно воспользоваться вторым замечательным пределом: 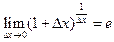 . Выберем
. Выберем 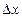 = – 100 h, тогда получим
= – 100 h, тогда получим 
2. Можно воспользоваться общими формулами решения разностных уравнений (см. пункт «Разностные уравнения»). Здесь m=1,  = (1 - 100h),
= (1 - 100h), 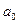 =100h. Характеристическое уравнение
=100h. Характеристическое уравнение  . Отсюда и следует решение (13.4). Частное решение уравнения (13.3) с правой частью имеет вид
. Отсюда и следует решение (13.4). Частное решение уравнения (13.3) с правой частью имеет вид 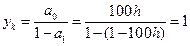 .
.
|
|
|
Предположим для определенности, что  =2. Тогда точные решения (13.2) и (13.24) примут вид
=2. Тогда точные решения (13.2) и (13.24) примут вид
 (13.5)
(13.5)
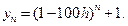
Функция y(x) очень быстро убывает от  =2 до своего предельного
=2 до своего предельного
значения 1. Так, например,  . Поэтому на начальном
. Поэтому на начальном
этапе мы, естественно, ожидаем, что для точного вычисления решения потребуется считать с малым шагом h< 0,001. Однако после, скажем, x=0,1 решение изменяется медленно и, по существу, равно 1. Так что интуитивно кажется, что метод Эйлера должен дать достаточную точность при сравнительно большом шаге h. Однако из (13.5) видно, что если h > 0,02, то 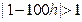 и значения
и значения 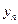 с увеличением номера шага начинают быстро расти, свидетельствуя о неустойчивости. Если сравнить точные решения (13.4) и (13.5), то видно, что частные решения уравнений (13.1) и (13.3) тождественно совпадают (и равны 1). Величина
с увеличением номера шага начинают быстро расти, свидетельствуя о неустойчивости. Если сравнить точные решения (13.4) и (13.5), то видно, что частные решения уравнений (13.1) и (13.3) тождественно совпадают (и равны 1). Величина  служит аппроксимацией экспоненциального члена
служит аппроксимацией экспоненциального члена 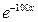 и действительно является хорошим приближением при малых h, но это приближение быстро становится неудовлетворительным, когда h достигает значения 0,02. И хотя этот экспоненциальный член после х = 0,1 фактические не вносит никакого вклада в решение, для сохранения устойчивости метод Эйлера по-прежнему требует, чтобы это слагаемое аппроксимировалось достаточно точно. Эта ситуация характерна для жестких уравнений: решение содержит слагаемое, вклад которого очень мал, однако обычные методы для сохранения устойчивости требуют, чтобы это слагаемое аппроксимировалось достаточно точно. Эта проблема очень часто возникает при решении систем уравнений. Рассмотрим, например, уравнение второго порядка:
и действительно является хорошим приближением при малых h, но это приближение быстро становится неудовлетворительным, когда h достигает значения 0,02. И хотя этот экспоненциальный член после х = 0,1 фактические не вносит никакого вклада в решение, для сохранения устойчивости метод Эйлера по-прежнему требует, чтобы это слагаемое аппроксимировалось достаточно точно. Эта ситуация характерна для жестких уравнений: решение содержит слагаемое, вклад которого очень мал, однако обычные методы для сохранения устойчивости требуют, чтобы это слагаемое аппроксимировалось достаточно точно. Эта проблема очень часто возникает при решении систем уравнений. Рассмотрим, например, уравнение второго порядка:
 . (13.6)
. (13.6)
Общее решение (13.6) имеет вид  . Так что решением,
. Так что решением,
удовлетворяющим начальным условиям y(0) = 1,01, y’(0) = - 2, является функция
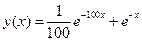 . (13.7)
. (13.7)
После того как х достигнет значения порядка 0,1, вклад первого члена в решение будет очень мал. Если, тем не менее, применить к соответствующему уравнению (13.6) системы первого порядка метод Эйлера, то мы столкнемся с той же самой проблемой, что и в предыдущем примере. Придется выбрать шаг достаточно малым, чтобы точно аппроксимировать член 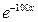 , несмотря на то, что его вклад в решение очень мал.
, несмотря на то, что его вклад в решение очень мал.
|
|
|
Преобразуем (13.6) в эквивалентную систему двух уравнений первого порядка.
Сделаем замену переменных и получим систему уравнений
y’=p(x);
p’= -101p -100y. (13.8)
Применим метод Эйлера, получим систему разностных уравнений
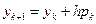
 . (13.9)
. (13.9)
Т.к. известно точное решение (22.7), то после дифференцирования следует
р(х)= 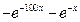 . Применим второй замечательный предел
. Применим второй замечательный предел  два раза и выберем
два раза и выберем 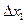 = –100 h,
= –100 h,  = –h, получим решение разностного уравнения
= –h, получим решение разностного уравнения
 ,
,
 . (13.10)
. (13.10)
Рекомендуем читателю сделать проверку, т.е. подставить получившееся решение в систему (13.9) и убедиться, что равенства стали тождествами. Таким образом, экспоненты приближаются двумя степенными функциями и очевидно значение шага h=0,02 велико, так как 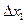 = 100h=2, и не о каком предельном переходе не может быть и речи!!!
= 100h=2, и не о каком предельном переходе не может быть и речи!!!
Кроме того, на этой задаче можно продемонстрировать, как влияют различные способы разностной аппроксимации.
Для разностной аппроксимации уравнения (13.6) применим трехточечный шаблон. То есть три последовательные точки  ,
, 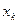 ,
,  , h =
, h =  -
- 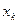 ,
,
0 < h < 1.
Первая производная имеет одно из двух представлений:
 или
или  .
.
Вторая производная имеет вид
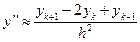 .
.
Для уравнения (13.6) можно записать, например, два разностных уравнения


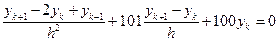 ;
;


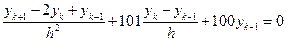 . (13.11)
. (13.11)
Эти уравнения различаются подчеркнутыми слагаемыми. Решение (13.10) удовлетворяет второму разностному уравнению (13.20) и не является решением первого уравнения.
Первое уравнение можно переписать в виде
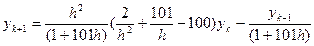 .
.
Характеристическое уравнение имеет вид
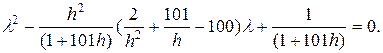
Здесь
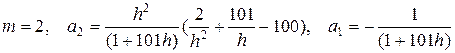 ,
,
приведение к общему знаменателю и дальнейшие упрощения специально не производятся, чтобы читатель мог проследить происхождение слагаемых из первого уравнения (13.11).
Решение первого разностного уравнения имеет вид:  .
.
При h = 0,01, 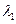 = - 0,2805,
= - 0,2805, 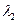 = 1,773 >1, второе слагаемое в решении растет. Шаг слишком большой, так как
= 1,773 >1, второе слагаемое в решении растет. Шаг слишком большой, так как 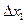 = -100h = -1. При h=0,0001,
= -100h = -1. При h=0,0001, 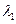 = –0,4121,
= –0,4121, 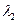 =2,402>1, первое слагаемое убывает, а второе растет.
=2,402>1, первое слагаемое убывает, а второе растет.
Второе уравнение (13.11) можно переписать в соответствии с теорией разностных уравнений:
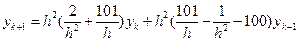 .
.
Здесь m=2,  ,
, 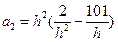 .
.
Характеристическое уравнение имеет вид
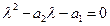
Его корни 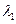 =1-100h <1,
=1-100h <1, 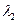 =1-h <1, что совпадает с (13.10).
=1-h <1, что совпадает с (13.10).
|
|
|
Приведенный пример демонстрирует сущность проблемы жесткости, возникающей при решении систем уравнений. Обычно в таких задачах независимой переменной является время, а в моделируемой физической проблеме возникают быстро затухающие переходные процессы, с которыми численной схеме приходится иметь дело и после того, как они уже практически ничего не вносят в решение. Общий подход к решению проблемы жесткости заключается в использовании неявных методов.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 801; Нарушение авторских прав?; Мы поможем в написании вашей работы!