Врахування граничних умов

Матричне рівняння (5.33 чи 5.14) – рівняння рівноваги для всієї системи, воно зв'язує зовнішні сили Q з вузловими переміщеннями q системи. У розгорнутому виді це будуть добре відомі в будівельній механіці стрижневих систем рівняння методу переміщень.

Однак скористатися безпосереднім рівнянням (5.33) не можна. Це зв'язано з тим, що при виводі матриці жорсткості ніде не фігурують умови закріплення системи в просторі, як твердого тіла. Тому кожне вузлове переміщення вектора q буде залежати від невизначених значень переміщень конструкції, як абсолютно твердого тіла. В силу цього матриця жорсткості всієї конструкції K особлива; її ранг менше її порядку на число ступенів системи як твердого тіла.

Щоб зафіксувати систему в просторі, треба ввести умову що переміщення в місцях опорів дорівнюють нулю. У просторовій конструкції мінімальна кількість переміщень, рівних нулю які дозволяють зафіксувати систему в просторі, дорівнює шести. У плоскій системі досить покласти три переміщення, рівних нулю, щоб виключити переміщення системи як твердого тіла.

Щоб зафіксувати систему в просторі необхідно відповідні невідомі у векторі вузлових переміщень 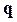заздалегідь прирівняти до нуля. Цим самим ми задовольнимо кінематичним граничним умовам закріплення конструкції. З іншого боку, цей факт треба відобразити у матриці K рівняння (5.33), викресливши рядки і стовпці, номери яких співпадають з номерами нульових переміщень.

Якщо пронумерувати невідомі переміщення так щоб в рівняннях МСЕ (5.33) спочатку йшли переміщення, які мають не нульові значення, то (5.33) можна записати так:

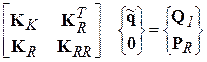, (5.41)

де: 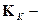частина матриці жорсткості, що залишилася після викреслювання стовпців і рядків відповідних нульовим переміщенням;

- вектор вузлових переміщень системи, який не містить переміщень апріорі рівних нулю;

Q₁ - вектор вузлових сил системи, без реакцій опор;

P_R - вектор реакцій опор;

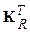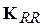і - викреслені стовпці;

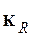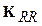і - викреслені рядки.

Тепер рівняння (5.41) можна записати у вигляді:

, (5.42)

де: K _k - зменшена матриця жорсткості системи.

Матричне рівняння (5.42) аналогічно рівнянню (5.41), але не містить переміщень системи як абсолютно твердого тіла. Матриця K _k неособлива і має зворотну матрицю 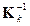. Розв’язок системи (5.35) дає значення переміщень:

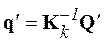(5.43)

З рядків, викреслених з матриці К, викресливши стовпці, що містять нульові переміщення, одержують матрицю , що дозволяє обчислити реакції опор, як це видно з (5.41)

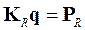(5.44)

5.7. Вектор еквівалентних вузлових сил

Вектор еквівалентних вузлових сил елемента знаходять за матричною формулою (5.35), яка отримана слідуючи принципу можливих переміщень. Аналітичні вирази компонентів вектора звичайно одержують паралельно з виводом виразів компонентів матриці жорсткості. З компонентів вектора еквівалентних сил, для відомих випадків навантаження, одержують формули обчислення значень еквівалентних вузлових сил. У публікаціях, там, де наведена матриця жорсткості, звичайно даються і вирази компонентів вектора еквівалентних вузлових сил.

Глобальний вектор вузлових сил одержують за формулою

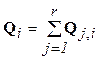, (5.45)

де: Q _i – і компонента глобального вектора еквівалентних вузлових сил;

Q _j,i – компонента вузлової сили i -го напрямку j -го елемента;

i – номер вектора навантаження (глобальний).

Підсумовування в (5.45) поширюється на всі r елементів для яких зв'язок і є загальним.

5.8. Деформації і напруги

Коли рівняння дискретної задачі (5.33) розв’язані, тобто отримані значення невідомих ступенів свободи, можна отримати для кожного з елементів координатну функцію u = 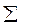Ф_jq_j (див. 5.19 чи 5.29).

Потім, використовуючи класичні залежності механіки твердого тіла, отримують компоненти напружено-деформованого стану.

Відносні деформації отримують за залежністю 5.26:

Зв'язок між напругами і деформаціями виражається законом Гука (5.25):

Тут B - матриця операторів диференціювання;

D - матриця пружних констант.

Звичайно приведені залежності перетворюються з урахуванням типу апроксимуючих функцій Ф_j, до виду:

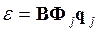(5.46)

де: Ф _j - матриця апроксимуючих функцій елемента;

q _j - матриця ступенів свободи

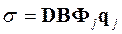(5.47)

Залежності (5.46) і (5.47) дають можливість обчислити напруги і деформації за відомими значеннями ступенів свободи.

5.9. Алгоритм комп’ютерного розрахунку за методом скінченних елементів

Дата добавления: 2015-05-26