Загальна характеристика. Дискретно-континуальний метод (ДКМ) або метод смуг є варіантом МСЕ в якому дискретизація виконується відносно тільки однієї осі

Дискретно-континуальний метод (ДКМ) або метод смуг є варіантом МСЕ в якому дискретизація виконується відносно тільки однієї осі. По другій – розв’язок є аналітичним, неперервним.

Механічну ідею методу покажемо на прикладі прогонової будови (рис.5.7) яка складається з двох балок довжиною L та плити проїзної частини шириною В. За принципами ДКМ представимо плиту прогонової будови системою елементів (поз.1) шириною b = В/n і довжиною, яка співпадає із прольотом L (тут n – кількість елементів плити)..

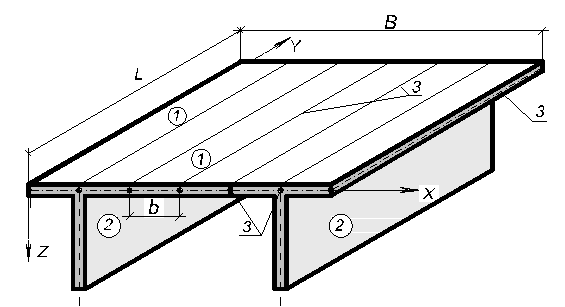
Рис. 5.7. Модель методу смуг

Балки прогонової будови моделюються плоскими елементами (поз.2) висота і довжина яких є такими, як і у реальної конструкції. Елементи моделі об’єднуються між собою вузловими лініями (поз.3).

Невідомі ступені свободи є розподіленими вздовж вузлових ліній. (Характер розподілу ступенів свободи і їх числові значення залежать від виду краєвої задачі.) Те що елементи об’єднані по вузловим лініям, а ступені свободи розподілені вздовж них дає можливість отримати аналітичний континуальний розв’язок відносно однієї із координат, відносно другої, модель як і в МСЕ є дискретною.

Модель є ефективною для конструкцій витягнутих вздовж однієї із координат, має декілька привабливих рис порівняно з класичною формою МСЕ:

· значно менша кількість невідомих що дає малий порядок системи лінійних рівнянь методу і можливість реалізації на комп’ютерах малої потужності;

· можливість аналітичного обчислення невідомих в довільних точках вздовж вузлових ліній;

· немає порушень сумісності деформацій вздовж вузлових ліній;

· модель дає досить прості алгоритми програм для розрахунку балкових прогонових будов, таких, як наприклад коробчастого перерізу.

Метод було розроблено О.В.Александровим у 1963 р для розрахунку складчастих систем. Пізніше, в 1968 р. А.К.Ченг використав ідею дискретно-континуального розв’язку і отримав в МСЕ специфічні скінченні елементи, які він назвав «смугами», а сам метод – методом скінченних смуг.

5.10.2. Скінченний елемент ДКМ в стані згину

Елемент виділяється двома вузловими лініями i та j (рис. 5.8а.). Розміри елемента: товщина t, ширина b, довжина L. Довжина елемента співпадає з довжиною конструкції. Ширину b вибирають відповідно вимогам точності розв’язку.

Елемент має постійні характеристики, різні в двох ортогональних напрямках.

	Рис.5.8. Скінченний елемент ДКМ, що знаходиться в стані згину

Задача ставиться в переміщеннях. За ступені свободи обрані чотири переміщення. На кожній вузловій лінії прикладаються два переміщення: нормальне до площини пластини w і кутове (рис. 5.8б.). Вектор ступенів і одного елемента має 4 компоненти:

, (5.48)

Йому відповідає вектор вузлових сил:

(5.49)

Кожна ступінь свободи подається у вигляді розкладання в ряд по фундаментальним функціям

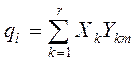; m = 1, 3, 5, r, (5.50)

де: - апроксимуючі функції, що залежать від x, поліноми Ерміта 3-го ступеня;

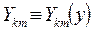- фундаментальні функції, що залежать від y;

r - кількість утримуваних членів розкладання.

Функцію вибирають використовуючи аналогію між вигином балки на пружній основі і вигином елемента, підтримуваного з двох сторін сусідніми елементами. Диференціальне рівняння вигину балки на пружній основі має вид:

, (5.51)

де a - параметр який визначається з характеристичного рівняння.

Загальний інтеграл однорідного диференціального рівняння (5.51) має вигляд:

, (5.51)

де 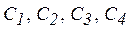- довільні постійні, які визначаються відповідно до граничних умов на кінцях інтервалу.

Для випадку граничних умов вільного обпирання довільні постійні 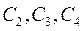- дорівнюють нулю, і, таким чином, функція здобуває більш просту форму:

(5.52)

Матрицю жорсткості елемента одержують за звичайною процедурою методу скінчених елементів мінімізацією відповідного функціонала.

Прийнято пружного функціонала, що відповідає крайовій задачі згину ортотропних пластин

(5.53)

Відповідний пружній функціонал крайової задачі

П (w)=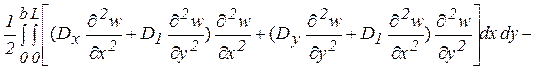

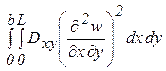- , (5.54)

де циліндричні жорсткості мають значення:

; ;

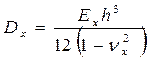; (5.55)

Координатна функція відповідно (5.50) і (5.52) має вид , (5.56)

Вносячи координатну функцію у вираз пружного функціонала і диференціюючи по ступенях свободи 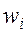, , 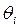, , одержуємо матрицю жорсткості елемента в стані згину, її розмір 4 х 4.

Загальна форма коефіцієнтів матриці жорсткості (після диференціювання по ступенях свободи) така

k_ij = +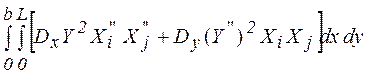

+ (5.57)

Дата добавления: 2015-05-26