Умовний екстремум 3 страница

2) Підінтегральна ф-ія – непарна відносно sin x, тоді роблять підстановку cos x = t.

3) Підінтегральна ф-ія – непарна відносно cos x раціоналізується за допомогою підстановки sin x = t.

4) Підінтегральна ф-ія R(sin x, cos x) – парна по sinx, cosx сукупно, тобто R(-sinx,-cosx)=R(sinx,cosx). В цьому випадку використовують підстановку tgx=t або ctgx=t.

5) Підінтегральна ф-ія R(tgx) раціоналізується підстановкою tgx=t. В інтегралах ò sin²ⁿx×cos^2mxdx рекомендується скористатися формулами зниження степеня

21.Визначений інтеграл як границя інтегральної суми

Означення: Якщо існує скінченна границя інтегральних сум S_n при l_і­­à0 і не залежить ні від способу розбиття [a;b] на частини Dх_і, ні від вибору точок x_і, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:

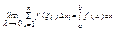
За означенням, визначений інтеграл 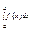– число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування.

Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною.

22. Формула Ньютона-Лейбніца

Якщо ф-ія F(x) є якою-небудь первісною від перер. ф. f(x), тобто F’(x)=f(x) для всіх x з проміжком [a;b] то справедлива формула Ньютона:

23.Геометричний зміст визначеного інтегралу

Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування.

24.Методи обчислення визначеного інтегралу

1)Підстановка у визначеному інтегралі. Якщо: f(x) – неперервна для xÎ [a;b], а ф. x=j(t)та її похідна x’=j’(t)неперер. на відрізку [a;b] при чому 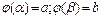, то справедлива рівність

2) Інтегрування частинам у визначеному інтегралі. Якщо ф-ії U=U(x) та V=V(x) мають неперервні похідні для xÎ[a;b], то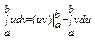

25. Властивості визначеного інтеграла

1) Якщо f(x) ³ 0 і інтегрована для xÎ[a,b], b>a, то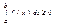

2) Якщо f(x), g(x) – інтегровані та f(x) 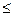g(x) для xÎ[a;b], a<b, то: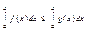

3) Якщо f(x) інтегровані на [a;b] такому, що (a<b) то: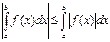

4) Якщо f(x) – інтегрована та m£f(x)£M, для xÎ[a;b], b>a, то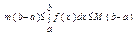

5) Якщо ф-ія f(x) – неперервна для xÎ[a;b], b>a, то знайдеться така точка CÎ [a;b], що: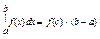

6)Якщо ф. 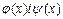диферент. В т. xє(a;b) i f(t) неперер. При 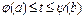, то

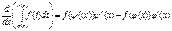
26.. Властивості невизначеного інтеграла

a)Властивості, що випливають з означ.:

1) похідна від невизначеного інтеграла дорівнює підінтегральній ф-ії:

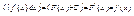
2) Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.

3)

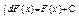
b)Властивості, що відображають основні правила інтегрування:

4) Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла.

5) Невизн. інтеграл від суми функцій дорівнює сумі невизначених інтегралів від цих функцій, якщо

27.Невласні інтеграли з нескінченими множинами інтгруання (першого роду)

Нехай ф. f(x) визнач. На пром.. [a; ) і інтегрована на будь-якій[a;b],де 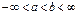, тоді якщо існує скінчена границя 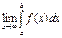її наз. невласним інтегралом I роду і познач. 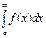; таким чином з означ.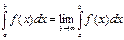

У цьому випадку інтегр. наз. збіжним, а підінтегр. ф. f(x) інтегрованою на пром. [a; 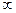), якщо границя не існує або нескінченна то інтеграл наз. Також невласним або розбіжним.

Аналогічно визнач. Невласний інтеграл на пром. (- 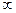;b] ;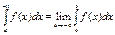

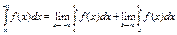, де с=const, c є R

28.Ознаки збіжності невласних інтегралів першого роду

1)Якщо на [a; 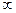) ф. f(x) та g(x) неперер. І задовольняють умові 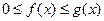то із збіжності інтегр. 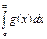випливає збіжність інтеграла і із збіжності інтеграла випливає розб.

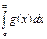
2)Якщо існує границя 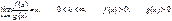, то інтеграли та 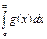або одночасно збігаються або розбігаються(гранична ознака порівняння)

3)якщо інтегр. 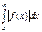збігається то збігається і інтегр. 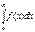при чому в цьому випадку він наз. абсолютно збіжним

29.Невласні інтеграли від необмежених функцій (другого роду)

Нехай ф. f(x) визнач. на пром. [a;b), т х=b наз. особливою т. ф. f(x), якщо f(x) 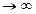при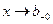

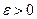Нехай ф. f(x) інтегрована на відрізку від [a;b- ] при довільному , такому що 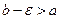, тоді якщо існує скінченна границя 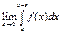то її наз. невласним інтегралом II р. і познач. 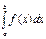. Отже за означенням .

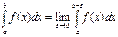У цьому випадку кажуть, що інтеграл існує або збігається, якщо границя нескінчена або не існує то інтеграл також наз. Невласним, але розбіжним.

Анологічно, якщо x=a особлива т., то . Якщо f(x) необмежена в околі якої небудь внутрішньої т. С є (a;b)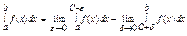

30.Наближене обчислення визначених інтегралів

Нехай від заданої та непер. на [a;b] ф-ції у=f(x) треба обч. 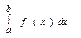. Поділимо [a;b] т. а=х₀, х₁, х₂,…,х_n-1, x_n=b ф-ції на n рівних частин завдовжки . Знач. ф-ції f(x) у т. х_і, і=(0,n) познач. так: у₀=f(x₀), у₁₌ f(x₁),…, у_n=f(x_n)

Формула трапецій

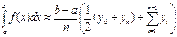Формула Сімпсона

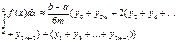
31. Означення числового ряду. Сума числового ряду

Рядом наз. вираз 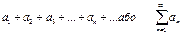(1), тобто сума з нескінченою кіл-стю доданків кожний доданок ряду (1) наз. його челоном.

Якщо всі члени ряду (1) задані числами то цей рчд наз. числовим.

Приклад числових рядів:

1)геометричний 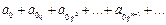де 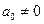, q- задані числа

2)гармонічний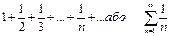

3)узагальнений гармонічний 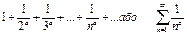, а- задане число.

Суму 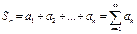наз. n-ою частковою сумою числового р.(1), а границю 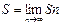наз. Сумою всіх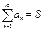

32.Властивості рядів. Збіжність числового ряду

Теорема: Якщо ряд 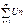збіжний, то:

Властивості рядів:

1)числовий ряд 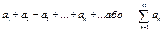(1) збігається т.і т.т., коли 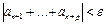(критерій Коші)

2)якщо р.(1) збігається, то загал. член , це необхідна умова збіжності ряду.

3)р. (1) збігається т.і т.т., коли збігається його n-ий залишок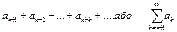

4)для двох збіжних рядів 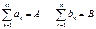і чисел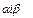 , тобто збіжні. можна почлено додаватиЮ а спільний множник можна виносити за знак суми.

5)у збіжному ряді ожна довільно будувати(брати у дужки,не переставляючи местами на збіжність та на його суму це не впливає).

33.Умови збіжності додатних рядів

Означення: знакододатний ряд – ряд вигляду U₁+U₂+…+U_n+…, всі члени якого є додатними(невідємними)

Додатній ряд 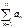є збіжним (розбіжним) якщо:

1) Ознака порівняння рядів.

Існує збіжний(розбіжний)додат.р. 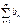для якого 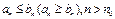(перша ознака порівняння)

або 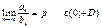(друга ознака порівняння)

2) Ознака Даламбера:

Якщо для знакододатного ряду

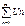
існує

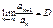то, якщо:D>1, ряд – розбіжний; D<1, ряд – збіжний

3) Радикальна ознака Коші.

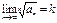k<1, ряд – збіжний; k>1, ряд – розбіжний

4) Інтегральна ознака Коші.

Беремо ò від 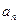-члена ряду. Якщо невласний інтеграл збіжний, то ряд – збіжний, якщо ж розбіжний, то ряд – розбіжний.

34. Знакозмінні ряди. Ознака Лейбніца.

Знакозмінні ряди це ряди вигляду: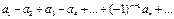

Ознака Лейбніца:

Знакозмінний ряд є збіжним, коли

1)

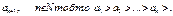
2)

35.Абсолютно та умовно збіжні ряди

Числовий ряд 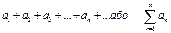(1) із довільними членами наз. Абсолютно збіжним, якщо збігається ряд 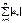, кожний абсолютно збіжний ряд є також збіжним, але не навпаки.

Р. (1) наз. умовно збіжним,якщо він є збіжним, проте не абсолютно. В абсолютно збіжних рядах можна переставляти місцями члени, що не впливає на його суму. Абсолютно збіжні ряди 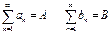можна перемножати за правилом Коші. 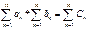, де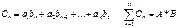

36. Функціональні ряди. Основні поняття

Ряд (1), членами якого є функції 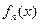, визнач. в одній і тій же самій обл. наз. функціональним рядом. Якщо аргументу X надати конкретного значення 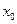, то одержимо числовий ряд.

Множину X значень аргументу х для яких ф.р.(1) збігається наз. обл. збіжності цього ряду.

Ф.р. наз рівномірно збіжним на множен. Х, якщо для як завгодного малого 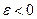можна вказати такий порядковий номер члену ряду 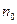Ю що при 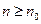виконується нерівність .

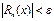Ознака Веєрштраса:

збіж.ч.р., якщо при всіх х є Х, для членів ф.р.(1) виконується нерівність , то аткий ф.р. рівномірно збігається на обл. Х

37. Степеневі ряди. Теорема Абеля. Радіус збіжності степеневого ряду

Степеневі ряди. Означення: Функціональний ряд вигляду a₀+a₁x+a₂x²+…+a_nxⁿ+… називається степеневим рядом, його загальний член U_n(x)=a_nxⁿ, а числа а₀,а₁,а_2,...,а_n,... – називають коефіцієнтами степеневого ряду. Степеневий ряд можна записати як:

Степеневий ряд може мати вигляд: a₀+a₁₍x-с)+a₂₍x-с)²+…+a_n(x-с)ⁿ+… Такий ряд за допомогою заміни х-с=у зводиться до звичайного степеневого ряду.

Теорема Абеля. Якщо степеневий ряд: 1) якщо при х=х₀, то він абсолютно збігається для будь-якого х, що задовольняє нерівність |x|<|x₀|; 2) якщо ряд розбігається при х=х₁, то він розбігається при всіх х, що задовольняють нерівніст |x|>|x₁|. Інтервал і радіус збіжності степеневого ряду. Як наслідок із теореми Абеля для Степ. Р. існує інтервал збіжності з центром в точці х₀. Означення: Інтервалом збіжності Степ. Ряду називається такий інтервал, у всіх внутрішніх точках якого ряд збігається абсолютно, а для всіх точок |x|>R ряд є розбіжним, при цьому число R>0 називається радіусом збіжності ряду.

Зауваження: На кінцях інтервалу збіжності, тобто в точках x=-R, x=R ряд може як збігатись, так і розбігатись. Це питання потребує спеціального дослілження в кожному випадку.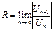

38.Теорема про рівномірну збіжність степеневого ряду

Степеневий ряд 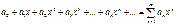(1), в межах інтервалу(-R;R) є рівномірною збіжним тому його можна почлено інтегрувати та диференціювати довільне число разів, тобто:

1)

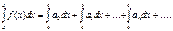
2)

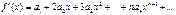
При цьому після інтегрування або диференціювання одержані ряди мають той самий радіус збіжності.

39.Розклад функції у степеневий ряд.

Нехай деяка ф. f(x) визначена і n-раз диференційована в околі т. x=0, також ця ф. має бути представлена степеневим рядом тобто розкладена в степеневий ряд:

Виразимо коефіцієнт степеневий ряд через ф. f(x).

Для цього скористаємось теоремою і знайдемо похідні ф f(x)

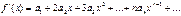
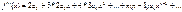
Враховуючи що в одержаних рівняннях x=0,маємо

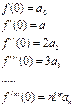
Тоді ; ; ; ;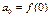

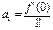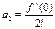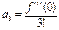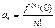
Підставляючи одержані коефіцієнти одержимо ряд:

ряд Маклорена

40.Розклад функції у ряд Маклорена.

Нехай деяка ф. f(x) визначена і n-раз диференційована в околі т. x=0, також ця ф. має бути представлена степеневим рядом тобто розкладена в степеневий ряд:

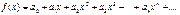
Виразимо коефіцієнт степеневий ряд через ф. f(x).

Для цього скористаємось теоремою і знайдемо похідні ф f(x)

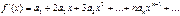
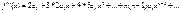
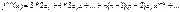
Враховуючи що в одержаних рівняннях x=0,маємо

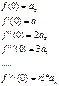
Тоді ; ; ; ;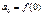

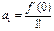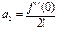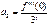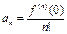
Підставляючи одержані коефіцієнти одержимо ряд:

ряд Маклорена

41. Розклад ф-ції у ряд Тейлора

Рядом Тейлора функції f (x) називається ряд вигляду:

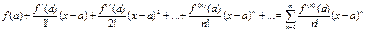
Тут a – центр розвинення; f (n)(a) – значення n -ї похідної в точці x = a;

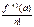– n -й коефіцієнт Тейлора, n = 0, 1, 2 ,....

42.Розклад функції у ряд Фур’є

Ф. f(x) наз. Такою, що відповідає умовам Діріхле на пром.[a;b], якщо вона на цьому пром..:

1)моє скінчене число розривів першого роду

2)має скінчене число екстремумів

3) 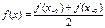в усіх точках пром.. [a;b]

Ф f(x), що відповідає умовам Діріхле [-П;П], може бути визначена в усіх точках цього проміжку рядом Фур’є

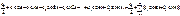, де

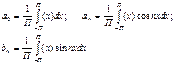n=1,2,3….

У випадку парної ф f(x) коеф. 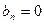для всіх n і ряд Фур’є має вигляд:

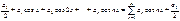, тоді

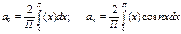
У випадку непарної ф f(x) коеф. 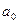та 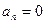і ряд Фур’є має вигляд:

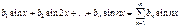
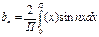, n=1,2,3….

43.Лінії рівня функції кількох змінних. Означення. Навести приклад

Лінією рівня наз. множина всіх точок площини, в яких ф-ія z=f(x;y) набуває однакових значень.

Рівняння ліній рівня записують у вигляді f(x;y)=C.

44.Використання універсальної підстановки при інтегруванні тригонометричних виразів

Інтеграл типу ,де R – раціональна функція своїх аргументів, заміною 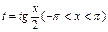зводяться до інтегрування функції, яка є раціональною відносно t.

При цьому ; ; ;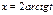

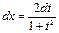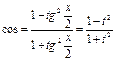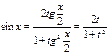
На практиці універсальну тригонометричну підстановку використовують,якщо sin x та cos x входять під інтегр. Вираз у невеликому стпені, інакше розрахунки бдуть дуже складні.

45.Метод невизначених коефіцієнтів

Нехай дріб 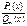правильний (тобто n<m), а знаменник дробу можна записати у вигляді

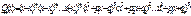, тоді

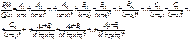
Де 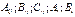- невизначені коефіцієнти

46.Поняття диференціального рівняння та його розвязоку

Диф. Рівнянням називається рівняння, яке містить шукану похідну ф-ції. Найбільший порядок похідних називається порядком диференційного рівняння.Найб. порядок пох. наз. порядком диф. р-ня.

Звич. ДР наз. нетотож. співвіднош. між шуканою ф-цією однієї змінної самою не залеж. змінною та пох. шук. ф-ції певних порядків.

Розв’язком ДР y’=f(x;y) наз. ф-ція у=j(х), яка при підстановці у ДР перетвор. його у тотож.

Розвязок, що містить довільні пост. наз загальним роз. ДР.

47.Теорма Коші про інтегрування та єдиність розв’зку рівняння першого порядку

Інтегральна крива це графік ф., що є розв’язком звичайного піддіференціального рів. Диф. рів. Не розв’язане відносно похідної має вигляд: 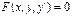(1)

Ф розв’язоно відносно похідної: (2)

Задачею Коші для рів. (1)або(2) наз. задачею відшукання функції y=y(x), xє(a,b), яка є розв’язком заданого рів. і задовольняє початкову умову задачі.

(3)

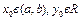
Загал. розв. диф. рів. (1)або(2) це така сукупність функцій 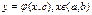, що для будь-якої допустимої фіксованої сталої С ф. 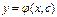є розв’язком даного рів. і для будь-якої допустимої початкової умови(3) існує така С, для якої ця ф. задовольняє дану початкову умову.

Якщо заг. розв. 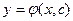записано у вигляді Ф(x,y,c)=0, то його наз. загал. інтегралом даного диф. рів.

Якщо ф. f(x,y) має в обл. Dнеперервні частинні похідні, то через кожну точку цієї обл. проходить єдина інтегральна крива диф.рів y’=f(x,y)

48.Рівняння з відокремленими змінними

Відокремлюваними диф. рів. з відокр. змінними наз.рів. виду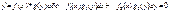

Де всі вказані ф. неперервні на певних проміжках. Такі рів. розв. відокремленням змінних:

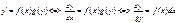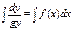; - заг.розв.рів., або задано у такому вигляді: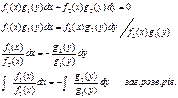

49.Однорідні диференціальні рівняння

Д.Р. називається однорідним, якщо його можна подати у вигляді: 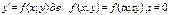або

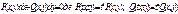тобто ф. P i Q є однорідними одного й того ж самого порядку.

Ці рів. можна записати у вигляді: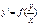

Ці рів. Можна звести до диф.рів. х відокремлюваними зміними за допомогою підстановки

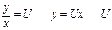-невідома ф. від х.

50.Лінійні диференціальні рівняння

Лінійним диф.рів. I порядку наз.рів. вигляду 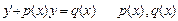-задані неперер. ф. пром.(a;b)

Рів. Розв’язується методом підстановки y=UV, де U та V невідомі ф. тоді

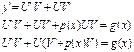
ф. V вибираємо таку, що 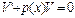і тоді

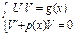
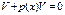
Тоді ф. U визнач. із рів.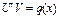

51. Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами

це рівняння виду ; p і q- числа(коеф.)

f(x)- задана ф.

Розглянемо випадок коли f(x)=0, то лін. диф. рів. наз. однорідним або без правої частини.

Такі рівняння розв’язують за правилом:

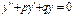
Дата добавления: 2015-05-26