Учет активных условий

Как правило, решение практических задач, связанных с оценкой качества и надежности изделий машиностроения, зависит не только от оперирующей стороны, но и от действий других субъектов системы. Каждая из сторон преследует собственные цели, не всегда совпадающие друг с другом. Неопределенность такого рода при принятии решений относят к классу поведенческих неопределенностей. Теоретической основой нахождения оптимального решения в условиях неопределенности и конфликтных ситуаций является теория игр. Игра - это математическая модель процесса функционирования конфликтующих элементов систем, в котором действия игроков происходят по определенным правилам, называемых стратегиями. Ее широкому распространению в последнее время способствовало как развитие ЭВМ, так и создание аналитического аппарата, позволяющего находить аналитические решения для широкого класса задач. Основной постулат теории игр - любой субъект системы по меньшей мере так же разумен, как и оперирующая сторона и делает все возможное, чтобы достигнуть своих целей. От реального конфликта игра (математическая модель конфликта) отличается тем, что она ведется по определенным правилам, которые устанавливают порядок и очередность действий субъектов системы, их информированность, порядок обмена информацией, формирование результата игры.

Существует много классов игр, различающихся по количеству игроков, числу ходов, характеру функций выигрыша и т.д. Выделим следующие основные классы игр:

- антагонистические (игры со строгим соперничеством) и неантогонистические. В первом случае цели игроков противоположны, во втором - могут совпадать;

- стратегические и нестратегические (в первых субъект системы действует независимо от остальных, преследуя свои цели, во-вторых субъекты выбирают единую для всех стратегию);

- парные игры и игры для N-лиц;

- коалиционные и бескоалиционные;

- кооперативные и некооперативные (в первых возможен обмен информацией о возможных стратегиях игроков);

- конечные и бесконечные (в первых - конечное число стратегий).

Наибольшее распространение в технических приложениях имеют парные стратегические бескоалиционные конечные некооперативные игры. Модель проблемной ситуации в этом случае имеет вид:

<U, V, W1, W2, R1, R2>

,где

U - множество стратегий оперирующей стороны (конструктора);

V - множество стратегий оппонирующей стороны (технолог и природа);

W1 и W2 - показатели качества игроков;

R1 и R2 - системы предпочтения игроков.

Системы предпочтения игроков, в свою очередь, основываются на двух ведущих принципах рационального поведения: принципе наибольшего гарантированного результата и принципе равновесия.

Первый основан на том, что рациональным выбором одного из игроков должен считаться такой, при котором он рассчитывает на самую неблагоприятную для него реакцию со стороны другого игрока.

Второй принцип гласит, что рациональным выбором любого игрока считается такая стратегия ux (или vx), для которой ситуация (ux, vx) обоюдовыгодна: любое отклонение от данной ситуации игры не является выгодным ни для одного из игроков.

Решается парная матричная игра (проектируемое изделие - меры и средства противодействия) с нулевой суммой (выигрыш одной стороны равен проигрышу другой) на основе рассмотрения платежной матрицы, которая представляет собой совокупность значений U и V (пара стратегий (u,v) U x V называется ситуацией игры), а также выигрышей Wij при парном сочетании всевозможных стратегий сторон.

Решение парной матричной игры может быть в чистых стратегиях, когда для каждой из сторон может быть определена единственная оптимальная стратегия, отклонение от которой невыгодно обоим игрокам. Если выгодно использовать несколько стратегий с определенной частотой их чередования, то решение находится в смешанных стратегиях.

Основные особенности использования методов теории заключаются в следующем. В качестве возможных стратегий со стороны проектируемой системы рассматриваются возможные варианты ее строения, из которых следует выбрать наиболее рациональный. В качестве стратегий противника рассматриваются возможные варианты его противодействия, стратегии их применения.

Необходимо отметить, что при рассмотрении игр с использованием адаптивной системы число ее стратегий может быть существенно расширено благодаря реализации "гибких" конструкторских решений. Анализ игровых ситуаций в этом случае может быть направлен не только на выбор рационального варианта проектируемого изделия, но и на определение алгоритмов рационального применения системы в конфликтной ситуации.

Другая особенность применения методов теории игр заключается в выборе решений, получаемых на основе анализа конфликтной ситуации. В теории игр доказывается теорема о том, что оптимальная стратегия для каждого из игроков является оптимальной и для другого. Так, если решение игры получено в чистых стратегиях (имеется седловая точка), то выбор решения однозначен. Например, если для парной антагонистической игры 3x4 составить матрицу, где элементами uij будут выигрыши (проигрыши) игроков, то седловая точка находится на пересечении максимина строк и минимакса столбцов

Стратегии	Стратегии B	min
A					строк
			-4		-4
max столбцов

Оптимальными стратегиями будут для A - 2, для B - 2. Цена игры равна 5. Отметим, что в случае наличия седловой точки ни один из игроков не может улучшить стратегию и стратегии называются чистыми. Отметим, что игра с чистыми стратегиями может существовать только при наличии полной информации о действиях противника.

Если же решение игры получено в смешанных стратегиях, то это эквивалентно созданию множества вариантов проектируемого компонента и использованию их с оптимальными частотам, соответствующими оптимальной смешанной стратегии. В случаях, когда не имеется полной информации о действиях противника, вводятся вероятности применения той или иной стратегии в виде векторов

P<n>=<p1, p2,..., pn> - для игрока A, где;

Q<m>=<q1, q2,..., qn> - для игрока B, где.

При этом игрок A выбирает стратегию в соответствии с принципом максимина по выражению:

, а игра B по принципу минимакса

Рассмотрим пример: пусть рассматривается принятие решения в игре 2x2, где игрок A знает вероятность стратегии 1, то есть p1, тогда очевидно вероятность стратегии 2 будет 1-p, соответственно стратегии игрока B будут q1 и 1-q1. Платежная матрица будет иметь вид:

		B
		q1	1-q1
A	p1	a11	a12
	1-p1	a21	a22

На основании матрицы и приведенных выше выражений составляется таблица:

Чистые стратегии игрока B	Ожидаемые выигрыши игрока A
	(a11-a21)p1 + a21
	(a12-a22)p1 + a22

Из таблицы видно, что ожидаемый выигрыш игрока A линейно зависит от вероятности p1 (в данном случае задача может быть решена графоаналитически). Тогда смешанная стратегия игрока А будет иметь вид

<p*1, p*2>,

то есть игроку A выгодно применять стратегию 1 с частотой (вероятностью) - p1, а стратегию 2 с частотой p2.

Очевидно, что разработка нескольких вариантов изделия сопряжена с большими затратами, не всегда реализуема и затрудняет использование системы. Поэтому при получении решения в смешанных стратегиях рекомендуются следующие случаи принятия окончательного решения:

- для дальнейшего проектирования выбирается тот вариант, который гарантирует максимальное качество (выбор по максиминной стратегии аналогично критерию Вальда);

- выбирается тот вариант, который в смешанной стратегии должен использоваться с максимальной вероятностью;

- реализуется несколько вариантов изделия с частотами, соответствующими смешанной стратегии (создание адаптивно-модульных конструкций).

Важное значение в задачах исследования качества адаптивных систем имеет не только решение игры, но и анализ платежной матрицы. Это особенно важно в тех случаях, когда решение в смешанных стратегиях не реализуется. Этот анализ может проводиться на основе: оценки возможных потерь эффективности в случае реализации чистой стратегии; определения дополнительных затрат на их компенсацию с помощью "гибких" конструкторских решений; оценки достоверности рассмотренных стратегий противодействия; определения возможности реализации компромиссных вариантов и т.д.

Для анализа конфликтной ситуации требуется на основе математической модели операции построить платежную матрицу [Wmn] =[Wij], где Wij характеризует качество изделия при выборе i-го варианта проектируемого изделия и при j-м варианте противодействия противника.

Решение может быть получено в чистых стратегиях, когда есть седловая точка. Условие седловой точки имеет вид

, где левая часть выражения - нижняя цена игры, правая - верхняя цена игры.

Если условие не выполняется, то седловая точка отсутствует и требуется реализация смешанной стратегии.

Решение в смешанных стратегиях состоит в реализации чистых стратегий с различными вероятностями, задаваемыми распределением:

для проектируемого изделия в виде вектора-столбца

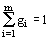
G = {gi}, где i = 1,2...m;;

для противодействия в виде вектора-строки

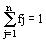
F = {fj}, где j = 1,2...n;

, где

gi - вероятность выбора стратегии ui;

fj - вероятность выбора стратегии vj.

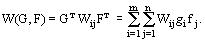Платежную функцию запишем в следующем виде:

, где индексом "т" обозначена процедура транспонирования.

Платежная функция W(G,F) всегда имеет седловую точку, т.е. всегда существует решение матричной игры. Это утверждение соответствует основной теореме теории матричных игр: каждая матричная игра с нулевой суммой имеет, по крайней мере, одно решение в чистых или смешанных стратегиях.

Последовательность решения игры следующая:

Анализируется платежная матрица на предмет исключения заведомо невыгодных и дублирующих стратегий.

Проверяется наличие седловой точки по условию седловой точки.

Если решение в чистых стратегиях отсутствует, то ищется решение в смешанных стратегиях с помощью методов линейного программирования или методом Монте-Карло.

Заключение

Для задач характерны неполнота и недостоверность информации, многообразие и сложность влияния социальных, экономических, политических и технических факторов. Эти обстоятельства не позволяют, по крайней мере, в настоящее время, построит адекватные математические модели решения задач по определению оптимального решения.

Литература.

1. Андреев В.Н., Герасимов Ю.Ю. Принятие оптимальных решений: Теория и применение в лесном деле. Йоэнсуу: Из-во ун-та Йоэнсуу, 1999. 200 с.

2. Беллман Р., Калаба Р. Динамическое программирование и современная теория управления. М.: Наука, 1969. 120 с.

3. Вентцель Е.С. Элементы динамического программирования. М.: Наука, 1964. 176 с.

4. Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.: Наука, 1988.

5. Калихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах. М.: Высшая школа, 1979. 125 с.

6. Кузнецов А.В., Холод Н.И., Костевич Л.С. Руководство к решению задач по математическому программированию. М.: Вышэйшая школа, 1978. 256 с.

7. Курицкий Б.Я. Оптимизация вокруг нас. Л.: Машиностроение, 1989. 144 с.

8. Киреева А.Я., Трошин Л.И. Сборник задач по математическому программированию. М.: МЭСИ, 1968. 168 с.

9. Жак С.В. Математическое программирование. Нелинейные и стохастические задачи. Ростов-на-Дону: РГУ, 1972. 90 с.

10. Злобинская Э.А. Методические указание по математическому программированию для студентов экономических специальностей. Часть 1. Барнаул: АСХИ, 1980.

11. Редькин А.К. Основы моделирования и оптимизации процессов лесозаготовок. М.: Лесная промышленность, 1988. 256 с.

12. Реклейтис Т. Оптимизация в технике. М.: Мир. Т. 1. - 279 с. Т. 2. - 320 с.

13. Юдин Д.Б. Задачи и методы стохастического программирования. М.: Сов. радио, 1979. 392 с.

14. Davis L.S., Johnson K.N. Forest management. New York: McGraw-Hill Book Company, 1987. 790 с.

15. Моисеев Н.Н., Математические методы системного анализа М. Наука 1981 487 с.

16. Е.С.Вентцель Исследование операций. Задачи, принципы, методология. М. Наука 1988 206 с.

Дата добавления: 2015-05-26