Композиция некоторых законов распределения

Композиция двух равномерных законов

Рис. 10.14. К построению закона Симпсона

Функцию распределения композиции двух равномерных законов в интервалах a ₁ < x ₁ < b ₁ и a ₂ < x ₂ < b ₂ можно получить как произведение постоянной плотности f (x ₁, x ₂) =1/[(b ₁ – a ₁)(b ₂ – a ₂)] на пло­щадь области D_y согласно рис. 10.13 б. Особый интерес представляет композиция двух СВ, равномерно распределенных в одном и том же интервале (рис. 10.14). Пусть a ₁ = a ₂ = 0, b ₁ = b ₂ = b, тогда функция распределения равна площади треугольника под x ₂ = y – x ₁ при 0 < y < b и как площадь дополнение к такому треугольнику при b < y < 2 b:

Рис. 10.15. Закон Симпсона

Плотность распределения суммы двух независимых реализаций СВ, равномерно распределенной в интервале длиной b имеет вид треугольника (рис. 10.15):

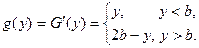
Это распределение называется законом Симпсона. Ему подчиняется, например, сумма результатов двух независимых измерений по грубой шкале. Сумма большого числа таких измерений подчиняется нормальному закону.

Композиция нескольких равномерных законов

Построим плотность распределения суммы нескольких независимых реализаций датчика случайных чисел, вернее, приближенную оценку, воспользовавшись файл-функцией построения статистических распределений SDL (Листинг 3.1). Каждое слагаемое будем разыгрывать 500000 раз, а число слагаемых увеличивать от 2 до 6, и построим графики статистических оценок плотностей распределения для каждого варианта (рис. 10.16):

>> for k = [12,2:6] A=rand(500000,k); [f,F,x]=SDL(sum(A,2)); plot(x,f), hold on, end

Качество приближения можно оценить по первому варианту с двумя слагаемыми, который практически совпадает с законом Симпсона. При трех слагаемых плотность распределения нелинейная, дальнейшее увеличение числа слагаемых приближает плотность распределения к нормальной кривой, которая вычислена объектом класса Norm_1 с параметрами m = 3, s = и выведена на этот же график красным цветом:

>> x=0:0.01:6;X=Norm_1(3,sqrt(1/2)); plot(x,fff(X,x),'r', x, fff(Norm_1(6,1),x),'r')

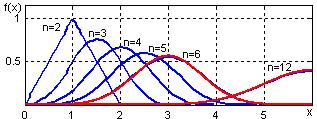
Рис. 10.16. Законы распределения суммы нескольких независимых СВ

Получение реализаций нормального закона с помощью датчика случайных чисел

Сумма n независимых СВ X с m_x = 1/2, D_x = 1/12 имеет характеристики m (n) = n /2, D (n) = n /12. При n = 6 МО и дисперсия равны, соответственно, 3 и 1/2, поэтому кривая плотности суммы шести слагаемых практически совпала с нормальной кривой с параметрами m = 3, s = 1/ . На этом основан простой способ получения реализаций стандартного нормального закона (m = 0, s = 1) с помощью датчика случайных чисел: сумму шести случайных чисел уменьшить на 3 и умножить на (или сумму n = 12 случайных чисел уменьшить на 6).

Можно считать, таким образом, что сумма n > 5 независимых реализаций СВ, распределенной равномерно в интервале [a, b], подчиняется нормальному закону с параметрами m (n) = n (b – a)/2, D (n) = n (b – a)²/12.

Композиция равномерного и нормального распределений

Композиция равномерно распределенной СВ X Î [a, b] и Z Î N (m, s) подчиняется закону распределения с плотностью

,

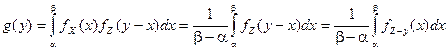где f_{Z – y} (x) – плотность нормального закона

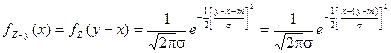
с тем же СКО, что у СВ Z, с центром в y – m. Таким образом, плотность композиции в точке y можно вычислить как вероятность попадания в интервал [a, b] СВ U Î N (y – m, s).

Построим график g (y) при a = 0, b = 10, m = 3, s = 2 в интервале значений аргумента [ m ± s] ×1,5. Воспользуемся классом Norm_1:

>> a=10;Z=Norm_1(3,2);y=Net(Z)*1.5;U=setval(Z,y-3);g=Ver(U,[0 a])/a;plot(y,g,'r')

Выведем также графики плотностей слагаемых СВ (рис. 10.17):

>> hold on, plot(y,f(Z,y)), plot([0 0 a a],[0 1/a 1/a 0], 'k')

Рис. 10.17. Законы распределения нормального,
равномерного законов и их композиции

Композиция двух показательных распределений

Композицию СВ X ₁ и X ₂, распределенных по показательному закону с параметрами l₁ и l₂ найдем интегрированием произведений плотностей f (x ₁) = l ₁ e ^{–l1 x 1}, x ₁>0, f (x ₂) = l₂ e ^{– l2 x 2}, x ₂>0 по треугольнику :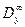

Это распределение называется обобщенным законом Эрланга первого порядка. Раскрыв неопределенность при l₁ = l₂ = l, получим закон Эрланга первого порядка:

y > 0.

Композиция нескольких показательных распределений

Рис. 10.18. Композиция в потоке событий

Композиция СВ X ₁, …, X_k, подчиненных показательному закону с параметром l, может означать время T_k ожидания k последовательных событий в потоке событий с интенсивностью l (рис. 10.18). Очевидно, T_k < t, если в интервале [0, t ] наступило не менее k событий. Вероятность наступления одного события в интервале длительностью t определяются по формуле Пуассона с параметром a = l t. Функция распределения СВ T_k – вероятность наступления не менее k таких событий:

F (t) = P (T_k < t) = .

Легко установить, что в выражении для производной F ¢(t) после сокращений остается только одно слагаемое:

.

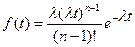Закон Эрланга

Часто представляет интерес не сама длительность ожидания k событий, а время ожидания следующего за ними (k + 1)-о события. В таких случаях говорят, что из потока пропускают k событий, а (k + 1)-е – обрабатывают. Закон распределения интервала между обрабатываемыми событиями

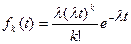
(10.11)

называется законом Эрланга k - о порядка. Этому закону подчиняется, например, длина свободного пробега танка на минном поле с определенной линейной плотностью l при условии, что k мин экипаж может обезвредить.

Создадим файл-функцию f_Erlang и построим с ее помощью графики распределения Эрланга порядков от 0 до 5 (рис. 10.19):

>> t=0:0.1:10; L=1.5; for k=0:5 y=f_Erlang(t,L,k);plot(t,y), hold on,end

Рис. 10.19. Плотность распределения закона Эрланга

При k = 0 закон Эрланга превращается в показательный закон и приобретает характерную особенность при малых значениях аргумента плотность показательного распределения в нуле совпадает с параметром l, тогда как вероятность события T Î[0, D t ] в распределениях Эрланга положительных порядков стремится к нулю при малых D t (как вероятность более, чем одного события в малом интервале пуассоновского потока). С другой стороны, t^ke^-t ® 0 при t ® ¥, следовательно, плотность распределения Эрланга имеет экстремум: при kt^{k – 1} – l t^k = 0, откуда следует Mo = k / l. МО и дисперсию найдем как ЧХ суммы k + 1независимых СВ, распределенных по показательному закону с параметром l:

, .

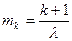Разность двух независимых показательных распределений

Закон распределения разности Y = X ₁ – X ₂ построим по первой формуле (10.11), изменив знак аргумента функции f ₂ на противоположный. Показательный закон определен для положительных аргументов, при y >0 неравенство x ₁ – y >0выполняется в интервале (y, ¥), при y < 0 – в интервале (0, ¥):

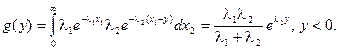
Этому закону подчиняется случайный интервал между двумя событиями из разных пуассоновских потоков. В случае l₁ = l₂ = l обе ветви можно представить единым выражением – законом Лапласа:

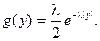
(10.12)

Композиция двух СВ, распределенных по закону Пуассона

Если X ₁, X ₂ независимые СВ, распределенные по закону Пуассона с параметрами a ₁, a ₂, возможные значения суммы Y = X ₁ + X ₂ – все целые числа (с нулем), а вероятности p_k = P (Y = k),можно выразить через параметры слагаемых СВ дискретным аналогом формулы (10.10):

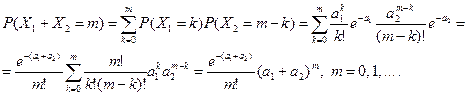
Закон Пуассона устойчив к композиции. Это значит, что совмещение нескольких простейших пуассоновских полей (суперпозиция полей) образует простейшее пуассоновское поле.

Осколочное поле как суперпозиция пуассоновских полей

Осколочное поле представляет собой пространственное совмещение полей, создаваемых разными фракциями. Эти поля могут быть неоднородными на всей проекции цели, но в пределах одного i -о УА плотность поля от k -й фракции можно считать зависящей только от координат центра разрыва относительно центра данного УА l_k (x_i, y_i, z_i). Попавший в i -й УА осколок k -й фракции выводит его из строя с вероятностью p_ki, зависящей для данного УА от массы q_k и скорости встречи v. Участок осколочного поля на проекции УА можно представить как суперпозицию простейших пуассоновских полей с плотностями «поражающих» осколков l_k (x_i, y_i, z_i) p_ki (q_k, v), а вероятность поражения – как вероятность наступления хотя бы одного события в распределении Пуассона с параметром

.

(10.13)

Композиция биномиальных распределений

Выборочный контроль качества изготавливаемых изделий проводится по схеме Бернулли: из партии наугад выбирают контрольную группу (n штук), в ней выявляют дефектные изделия, их количество сравнивают с критическим (приемочным) числом. При известной частоте дефектных изделий в партии (вероятности обнаружения дефекта p) число дефектных изделий в контрольной выборке X подчиняется биномиальному закону с параметрами n, p. В случае небольшого превышения критического числа обнаруженных дефектов берут вторую выборку (метод двукратной выборки). Если общее число дефектных изделий не превышает установленное второе критическое число, партия принимается. Речь идет о композиции двух СВ X ₁, X ₂, распределенных по биномиальному закону с параметрами, соответственно, (n ₁, p) и (n ₂, p). Число успехов в испытаниях Бернулли равно сумме индикаторов успеха в i -м опыте:

, ,

так как P (X = 1) = p в обоих опытах. Общее число успехов

Y = X ₁ + X ₂ =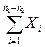

подчиняется биномиальному закону с параметрами n = n ₁ + n ₂ и p.

Таким образом, устойчивость относительно сложения – не только асимптотическое свойство закона Пуассона, аппроксимирующего биномиальное распределение, но фундаментальное свойство распределений, вытекающих из условий испытания Бернулли. Значит, оно должно быть присуще и другому «родственнику» биномиального закона (согласно локальной теореме Лапласа) – нормальному закону.

Дата добавления: 2015-06-25