Система обслуживания с ожиданием

Ниже в качестве объекта исследований будет использоваться СМО с ожиданием, имеющая m идентичных каналов обслуживания и простейший поток заявок с интенсивностью , у которой время обслуживания и время ожидания – случайные величины, распределённые по экспоненциальным законам с параметрам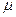и и 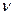соответственно.

Пусть - возможное состояние системы, характеризуемое тем, что в ней занято ровно 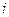каналов обслуживания, 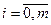, а возможное состояние системы характеризуется тем, что все m каналов обслуживания заняты и очередь состоит из 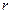заявок, где 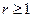. Рассматриваемую СМО можно было бы классифицировать как 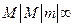(длина очереди не ограничена).

За бесконечно малый промежуток времени 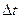система обслуживания с простейшим входным потоком заявок и экспоненциальными законами распределения времени обслуживания и времени ожидания либо остаётся в прежнем состоянии , либо переходит при в два соседних состояния – 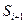или и при в одно соседнее состояние .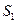

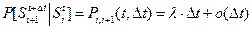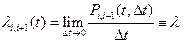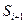Напомним, что для простейшего потока или .Переход из «младшего» состояния в «старшее» состояние зависит толь- ко от потока заявок, каждая из которых либо поступает в канал обслуживания, либо становится в очередь.

При (т.е. очереди нет!) переход из состояния в «младшее» состояние зависит лишь от освобождения каналов обслуживания. Если 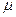- интенсивность обслуживания, то функция распределения времени обслуживания . Тогда

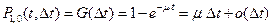и, следовательно, 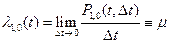- для одного канала, а при 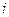занятых каналах .

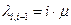Для 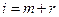, переход в «младшее» состояние, помимо завершения обслуживания заявки, может быть вызван также уходом из очереди одной заявки, если время ожидания превышает допустимое. В рассматриваемом случае закон распределения определяется интенсивностью 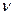ухода из очереди при наличии в ней одной заявки. Поскольку заявки, находящиеся в очереди, отказываются от обслуживания независимо друг от друга, то тогда суммарная интенсивность отказа заявок от обслуживания равна . В итоге плотность вероятности перехода системы из состояния в состояние 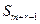равна сумме интенсивностей освобождения каналов обслуживания и отказа заявок от обслуживания: . Размеченный граф состояний будет выглядеть следующим образом:

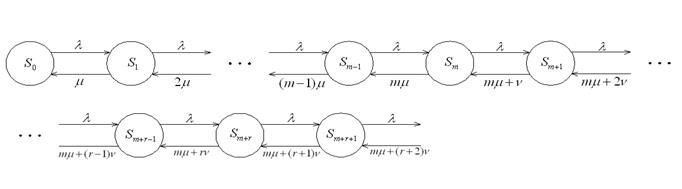
Воспользовавшись этим графом и правилами построения системы уравнений Колмогорова, получаем:

(5)

Поскольку на длину очереди нет ограничений, то в данном случае система ОДУ является бесконечной. Если в начальный момент времени 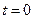система обслуживания находилась в одном из возможных состояний , то начальные условия для системы ОДУ будут выглядеть следующим образом: .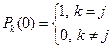

ЗАДАЧА 7. Построить математическую модель для СМО типа .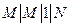

◄ Рассматривается одноканальная система с ожиданием, на вход которой поступает простейший поток заявок с интенсивностью 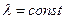, 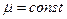- интенсивность обслуживания, количество мест в очереди на обслуживание ограничено () и заявка, поступившая в момент, когда в очереди уже находится заявок, покидает систему. Состояния СМО: 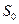- канал свободен, 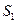- канал занят, но очереди нет; 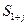- канал занят и в очереди находятся заявок, 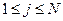. Единственной причиной отказа в обслуживании является отсутствие места в очереди и, значит, интенсивность ухода из очереди равна нулю, т.е. .

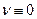Размеченный граф состояний

позволяет записать систему уравнений Колмогорова:

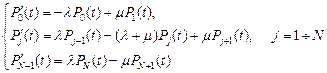(6)

Остаётся задать начальные условия: 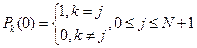и можно исследовать полученную систему ОДУ, составляющую основу математической модели рассматриваемой СМО. ►

Стационарные РЕЖИМЫ ФУНКЦИОНИРОВАНИЯ СМО представляют большой практический интерес. Математическая модель стационарного режима СМО формально является предельным случаем (при 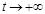) обычной математической модели процесса. При классических предположениях относительно описываемого процесса массового обслуживания сама эта математическая модель представляет собой задачу Коши для соответствующей системы ОДУ (уравнения Колмогорова) и является частным случаем математической модели процесса гибели-размножения.

Базируясь на результатах анализа стационарных режимов процессов гибели-размножения проведём анализ стационарного режима функционирования СМО с ожиданием как наиболее общего случая системы обслуживания.

СМО С ОЖИДАНИЕМ: каналов обслуживания, «нетерпеливые заявки», .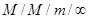

Анализ стационарного режима функционирования.

В стационарном режиме функционирования изучаемая система по-прежнему меняет своё состояние случайным образом, но вероятности состояний 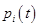уже практически не зависят от текущего времени, т.е. . Полагая в системе ОДУ (6) , получаем систему алгебраических уравнений, в которой 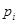характеризует относительное время пребывания СМО в состоянии :

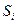(7)

причём Из первого уравнения где - называется приведённой плотностью потока заявок и определяет суммарное среднее число требований 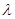, поступивших в СМО за среднее время обслуживания одной заявки 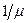, поскольку интенсивность простейшего потока 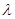определяет среднее число заявок, поступивших в СМО в единицу времени, а величина 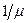, обратная интенсивности обслуживания 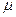, численно равная среднему времени обслуживания одной заявки. Ясно, что если за время обслуживания одной заявки поступает на обслуживание более одной заявки, то у СМО будет происходить неограниченный рост длины очереди. Помимо соотношения , из первых уравнений системы (7) получим Аналогично из последних уравнений системы: , где 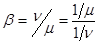- приведённая плотность ухода заявки из очереди (отношение среднего времени обслуживания одной заявки 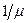к среднему времени ожидания в очереди ). Используя условие нормировки, получаем

(8).

Характеристики эффективности функционирования СМО:

– средняя длина очереди заявок на обслуживание (математическое ожидание числа заявок, находящихся в очереди):

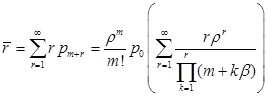. (9)

Поскольку требования уходят с интенсивностью 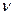, то из заявок, пребывающих в очереди, заявок в единицу времени покидают очередь (то есть СМО), не дождавшись обслуживания. Поэтому из поступивших в СМО в единицу времени 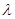заявок будет обслужено 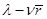заявок. Тогда абсолютная пропускная способность СМО , а относительная пропускная способность , поскольку характеризует вероятность того, что заявка, поступившая в СМО, будет обслужена;

 вероятность события, состоящего в том, что заявка покинет СМО необслуженной;

- вероятность того, что пришедшая заявка будет вынуждена ожидать обслуживания.

Среднее число занятых каналов обслуживания : .

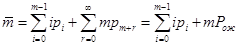С другой стороны, за единицу времени каналов обслуживают 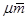заявок. Значит 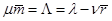или 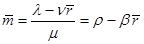.Так как непосредственное вычисление более громоздко, чем вычисление , то можно находить из последней формулы: 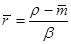.Аналогично можно получить: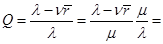 , то есть относительная пропускная способность равна отношению среднего числа занятых каналов к приведённой плотности потока заявок . Вероятность отсутствия требований в системе равна .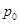

Дата добавления: 2015-06-25