Чистые системы обслуживания с ожиданием без потерь

Это СМО, в которой заявки не покидают очереди, то есть заявка имеет неограниченное время ожидания. Воспользуемся предыдущими результатами, учтя равенство нулю интенсивности ухода заявок из очереди: и . Из (8) получим:

(10)

Если , то есть приведённая интенсивность потока заявок 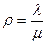не меньше числа каналов обслуживания m, то ряд в (10) расходится и поэтому 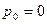. Но тогда из формул для стационарного режима следует, что . Это приводит к нарушению условия нормировки. Из этого следует, что стационарного режима нет (будет происходить неограниченное нарастание очереди и СМО не будет справляться с потоком требований!).

Если 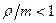, то ряд суммируется (геометрическая прогрессия!) и

(11)

Из (9) с учётом

(12)

Здесь использовано равенство 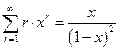при 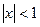, полученное из 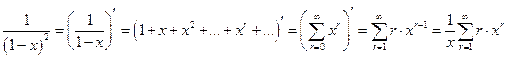за счёт равномерной сходимости ряда. После несложных преобразований из (12) следует

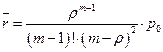(13)

Уточним, что поскольку 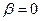, то для рассматриваемого случая

(14)

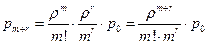(15)

ЗАМЕЧАНИЕ. Для одноканальной СМО (т.е. при 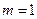) с неограниченной очередью:

, , , . (15а)

Редакционная пометка: создать отдельную таблицу для неограниченной очереди.

ЗАДАЧА 8. На железнодорожную сортировочную горку прибывают составы с интенсивностью 2 состава в час [1]. Среднее время обработки состава – 0.4 часа. Составы, прибывающие в момент, когда сортировочная горка занята, становятся в очередь в парке ожидания с тремя путями, на каждом из которых помещается один состав. Если все пути в парке ожидания заняты, то прибывающие состав ожидает свою очередь на внешней ветке. Найти:

1) среднее число составов, ожидающих обработки;

2) среднее время пребывания состава в парке ожидания;

3) среднее время пребывания состава на внешней ветке;

4) среднее время пребывания состава на сортировочной горке, включая время ожидания и время обслуживания;

5) вероятность того, что прибывающий состав займет место на внешней ветке.

◄ В системе один канал обслуживания (сортировочная горка), поэтому . Состояние - на горке нет составов, 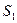- горка занята, но в парке ожидания составов нет, - соответственно 1, 2 или 3 пути заняты ожидающими сортировки составами (помимо одного состава, находящегося на сортировочной горке).

Интенсивность входного потока , интенсивность обслуживания 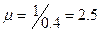, приведённая плотность потока заявок . Поскольку 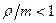, то система справляется с обслуживанием входного потока и, согласно (11), при . Значит .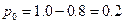

Среднюю длину очереди (в составах– “заявках”) найдем из (13) или (15а): .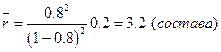

Поскольку рассматривается чистая модель с ожиданием, то 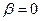. Используя формулы (15а), можно определить вероятность того, что прибывающий состав займет место на внешней ветке равна вероятности того, что длина очереди будет больше трех (все три ветки заняты!): . Значит в рассматриваемом случае .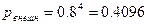

Среднее время ожидания на внешней ветке:

.

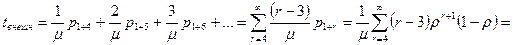
Первое слагаемое учитывает время ожидания обслуживания одним составом, 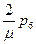- время ожидания обслуживания двумя составами и т.д.

Среднее время простоя в парке ожидания с тремя путями (на каждом из которых может находиться только один состав):

.

Суммарное среднее время ожидания обслуживания: .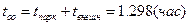

Среднее время обслуживания состава (общее время пребывания на сортировочной горке):

. ►

ЗАДАЧА 9. В предыдущей задаче рассмотреть случайналичия в парке ожидания 4 и 5 путей.Сравнить полученные результаты.

ЗАДАЧА 10. В турагентстве два менеджера проверяют готовность документов клиентов для покупки горящих путёвок в Париж или Лондон. Установлена объединённая очередь сразу к двум менеджерам и если один из менеджеров освобождается, то он начинает обслуживать ближайшего по очереди клиента. Интенсивность потока заявок (клиентов, желающих получить путёвку) для обоих направлений одинакова 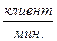. Менеджер тратит в среднем 2 минуты на обслуживание одного клиента.

В целях уменьшения очереди клиентов к менеджерам топ-менеджер решил закрепить за каждым менеджером своё направление (Париж или Лондон) и свою клиентскую очередь на обслуживание. Как скажется это предложение на длинах очередей на обслуживание? Насколько сократятся очереди на обслуживание, если время обслуживания клиента сократится до 1,5 минут?

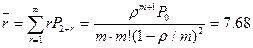
◄ 1) Случай общей очереди – два канала обслуживания (двух канальная СМО). Суммарная интенсивность потока заявок , , . Поскольку , то существует стационарный режим (т.е. существуют финальные вероятности) , среднее число заявок в очереди . Среднее время, проводимое заявкой в очереди (по теореме Литтла), . Если среднее время обслуживания сократится до 1,5 , то 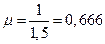и интересующие топ-менеджера характеристики будут равны: , , , .

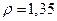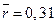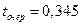
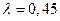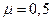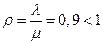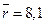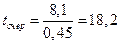
2) Две отдельные очереди – фактически две отдельно функционирующие одноканальные СМО, каждую из которых можно рассматривать отдельно. В этом случае интенсивность входящего потока , , . Стационарное положение существует. , , . Обращает на себя внимание быстрый рост длины очереди и времени ожидания клиентом начала обслуживания.

Если среднее время обслуживания сократится до 1.5 , то , , 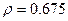, , , что означает только ослабление влияния неправильного управленческого решения.

КОММЕНТАРИЙ. На этом примере видно, как быстро возрастает длина очереди и время обслуживания при приближении 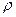к единице, т.е. когда СМО работает на пределе своих возможностей. ►

Система обслуживания с потерями (СМО с отказами). Задача Эрланга.

Заявка, поступившая в такую СМО в момент, когда все каналы обслуживания заняты, покидает систему. Значит - канальная система имеет конечное число состояний , очередь отсутствует: 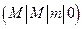. Математическая модель СМО имеет вид:

Чтобы избежать длинных выкладок, воспользуемся моделью СМО с ожиданием (см. выше), для чего достаточно принять, что интенсивность ухода из очереди , а значит (Тем самым обеспечивается мгновенный уход заявки из «очереди»). Тогда 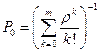, , 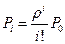 формулы Эрланга. Обозначим 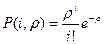, , 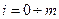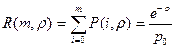. Тогда , .

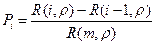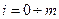При больших : 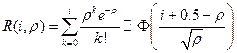, где 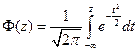 функция Лапласа.

Полагая 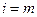(все каналы заняты), найдём вероятность отказа заявке в обслуживании (доля времени, когда все каналы заняты). Заявка, не получившая отказа, обязательно будет обслужена. Поэтому вероятность того, что заявка, поступившая в СМО, будет обслужена, есть как раз относительная пропускная способность : .

Среднее число занятых каналов : .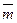

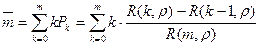Среднее число свободных каналов равно .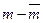

Среднее время пребывания требования в системе .

Среднее время простоя канала обслуживания 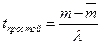. С другой стороны 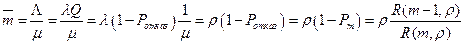, так как 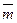есть отношение абсолютной производительности СМО (абсолютная пропускная способность СМО – среднее число заявок, обслуженных в единицу времени ) к интенсивности обслуживания 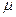(среднее число заявок, обслуживаемых в единицу времени (см. стр. 15)).

ЗАДАЧА 11. АТС обеспечивает не более 120 переговоров одновременно. Средняя продолжительность разговора 60 , вызовы поступают в среднем через 0.5 . Рассматривая АТС как многоканальную СМО с отказами и простейшим входным потоком 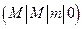, найти

1) 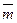- среднее число занятых каналов;

2) -относительную пропускную способность;

3) среднее время пребывания вызова на АТС (с учётом того, что разговор может не состояться).

◄ Т.к. , , , ,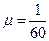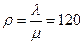то для стационарного режима функционирования СМО

,

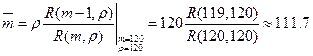поскольку 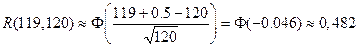и , .

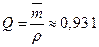Так как 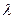есть интенсивность входного потока (число заявок в единицу времени), то 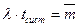(формула Литтла) или . Среднее время простоя канала . ЗАМЕЧАНИЕ. Обратим внимание, что в рамках рассматриваемой модели получено, что 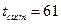сек, хотя в исходных данных средняя продолжительность разговора 60 - издержки «приближённости» модели .► Редакционная пометка - проверить значение 61сек, возможно надо 56 сек

ЗАМЕЧАНИЕ. В 1959г. Севастьяновым Б.А. доказано, что формулы Эрланга для финального распределения вероятностей состояний  канальной СМО с отказами справедливы не только при показательном, но и при произвольном распределении времени обслуживания.

Дата добавления: 2015-06-25