Применение теории игр к исследованиям природных систем

Второй класс задач значительно сложнее первого. По меньшей мере, некоторые элементы подсистем второго класса могут принимать собственные решения, иметь свои собственные цели. При этом возможен конфликт между решениями, выбранными различными элементами. Созданная теория игр (Льюс, Райфа,1961) может быть использована для решения одноуровневых многоцелевых задач.

Игровые постановки вопросов возникают в самых разнообразных случаях. Например, при эксплуатации природных ресурсов исследователь сталкивается с ситуацией, когда, несмотря на неполноту наших знаний о предмете исследований, необходимо принять решение о путях хозяйственного использования природных ресурсов.

Любые действия могут привести в будущем к ущербу, если неизвестные обстоятельства окажутся неблагоприятными. Требуется установить такой комплекс действий, при котором ущерб, могущий быть вследствие неизвестных обстоятельств, не превышал бы известных пределов, а хозяйственный эффект был бы оптимальным.

Для конфликтных ситуаций такого характера типично то, что одним «игроком» является человеческое общество, а другим - природа.

Пересечение интересов всегда было стержнем сюжетов в мировой литературе. Столкновение интересов является одним из предметов изучения нескольких отраслей науки: экономики, социологии, экологии.

Анализ подобного рода действий вызвал к жизни специальный раздел математики - теорию игр (Льюис, Райфа,1961). Под игрой подразумевается упрощенная, формализованная модель жизненной конфликтной ситуации.

Теория игр - это математическая дисциплина, которая устанавливает правила поведения в конфликтных ситуациях, обеспечивая достижение лучших (в некотором заранее заданном смысле) результатов. Эта дисциплина привлекла внимание исследователей своими разнообразными применениями в экономике, организации производства, военном деле и прочее. Применима она и к проблемам экологии и географии.

В общих чертах проблема состоит в следующем. Пусть индивидуум находится в положении, когда надо совершить некоторое действие. Хотя он может в некоторой степени управлять определенными факторами, но не имеет полной власти над ними.

В некоторых случаях конечный исход зависит как от случайностей (например, стихийные бедствия), так и от самих индивидуумов. Желательно иметь теорию, которая бы подсказывала общие принципы для руководства разумными действиями. С этой целью рассмотрим классификацию: определенность, риск, неопределенность.

При определенности происходит выбор решения, когда относительно каждого действия известно, что оно приводит к некоторому конкретному исходу.

При риске происходит выбор решения, когда каждое действие приводит к одному из множества возможных решений, причем каждый исход имеет определенную вероятность появления. При этом предполагается, что эти вероятности известны.

При неопределенности происходит выбор решения, когда может быть множество исходов, но вероятности этих исходов неизвестны.

Проанализируем эту классификацию с точки зрения применения математических методов.

Выбор решений при определенности - это широкая область. В качестве основного математического аппарата применяется классический анализ для отыскания максимальных или минимальных значений функций, о котором говорилось ранее.

В общем случае выбор решений при определенности сводится к следующему. Дано множество возможных действий и нужно выбрать одно (или все) действия, которые максимизируют (или минимизируют) некоторые показатели.

Примером выбора решений при определенности является задача о диете, которая решается методом линейного программирования.

Пусть имеется n продуктов: 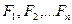- их названия. Диета - это суточное потребление каждого продукта:

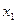- количество продукта , 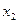- количество продукта 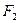и т.д.

С каждой диетой () можно связать содержание перечня питательных веществ и элементов, которые нас интересуют: жиры, белки, углеводы, железо, кальций, витамины А, B, C и т.д. Содержание в диете (), скажем, белков описывается линейным соотношением: 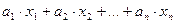. Здесь 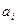содержание белка в потребленном продукте .

Согласно медицине для поддержания здорового образа жизни каждому человеку требуется минимальное количество питательных веществ, т.е.

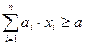
(2.19)

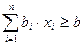
и т.д. для каждого вида питательных веществ.

Эти условия легко выполнить (т.е., получить много решений) для большого количества (т.е., потреблять много пищи, которая содержит вышеперечисленные питательные вещества). Но, при этом возникает опасность растолстеть и, кроме того, в реальной жизни существуют ограничения. Например, стоимость диеты ограничена денежной суммой P. В этом случае количество возможных решений резко сокращается, так как должно быть выполнено условие:

(2.20)

Здесь 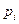- стоимость продукта .

Таким образом, задача о выборе диеты сводится к удовлетворению условий:

а) требованиям питательности,

б) требованиям стоимости.

Это типичная задача линейного программирования.

Итак, общая задача линейного программирования включает факторы:

1) операции, каждая из которых состоит в выборе n действительных чисел (например, диеты),

2) условия осуществимости (ограничения), представляющие собой линейные равенства и неравенства, которым могут быть подчинены возможные выборы,

3) связанный с каждым выбором показатель, равный взвешенному (среднему) всех n чисел, составляющих выбор (например, функции стоимости).

Задача заключается в нахождении набора чисел, удовлетворяющих условиям 2) и 3).

Теперь рассмотрим понятие «риск» в введенной классификации.

Взаимодействие человека и природы можно рассмотреть как игру двух игроков.

В результате рассмотрения игры вырабатывается такая рекомендация для разумного поведения (при играх с природой рассматриваются, прежде всего, действия человека), когда хозяйственный эффект оптимален. Теория игр предусматривает, что каждая из сторон будет делать определенные ходы, т.е., выбирать с течением времени ту или иную стратегию.

Обозначим стратегии - возможные варианты человека через , а стратегии противника (природы) - через .

Предположим, что человек выбирает стратегию , а природа стратегию , Выбор стратегий и однозначно фиксирует исход игры, который имеет численное значение 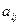. Эта величина представляет выигрыш игрока . Данная игра являет собой игру с нулевой суммой, что означает, что выигрыш игрока автоматически ведет к проигрышу такой же по сумме величины для игрока, который использует стратегию . Так как в рассматриваемом случае число стратегий со стороны человека , а со стороны природы , то мы будем иметь таблицу матрицы игры, где будут отражены все значения выигрышей любой пары стратегий и

(2.21)

В теории игр доказывается, что решение в области чистых стратегий (т.е., когда единственным оптимальным решением является одна стратегия со стороны человека и одна стратегия со стороны природы) возможно, когда в матрице имеется так называемая седловая точка, характеризующаяся следующим уравнением:

(2.22)

Элемент матрицы, характеризующий седловую точку (т.е., число в матрице на пересечении двух оптимальных стратегий), является оптимальным решением исследуемой задачи. Любое отклонение человека от стратегии, связанной с седловой точкой, дает решение, которое меньше по значению, чем оптимальное решение.

Уравнение (2.22) означает следующее. Если человек не хочет рисковать, то он, выбирая стратегию, должен рассчитывать на худший для себя вариант, т.е., что другая сторона (природа) выберет (в данной ситуации случайным образом) такую стратегию, при которой выигрыш человека будет минимальным. Следовательно, надо выбирать такую стратегию, при которой, рассчитывая на наихудший вариант со стороны природы, человек может иметь максимальный выигрыш. Все вышесказанное описывается левой частью уравнения (2.22). Аналогичные размышления со стороны противника (природы) при определенных коэффициентах матрицы игры приводят к правой части уравнения (2.22). Число в матрице, удовлетворяющее уравнению (2.22), носит название «цены игры». Если уравнение (2.22) выполняется, то «цена игры» может быть найдена в области чистых стратегий.

Ниже в качестве примера приведена матрица, имеющая седловую точку.

(2.23)

Первая строка соответствует стратегии 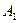, вторая строка соответствует стратегии , третья строка соответствует стратегии 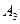, четвертая строка соответствует стратегии . Соответственно, первый столбец соответствует стратегии , второй столбец соответствует стратегии , третий столбец соответствует стратегии 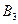, четвертый столбец соответствует стратегии .

(Индекс j направлен по оси X, индекс i направлен по оси Y).

Рассмотрим, как выполняется уравнение ().

В этом уравнении сначала анализируется левая часть уравнения, т.е., выражение ().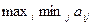

Для этого рассмотрим построчно таблицу и выпишем минимальное значение числа в каждой строке. В первой строке (-5,3,-2,-1) минимальное значение равно (-5). Во второй строке (4,2,3,2) минимальное значение равно (2). В третьей строке

(4,-3,2,2) минимальное значение равно (-3). В четвертой строке (2,1,-2,-3) минимальное значение равно (-3). Теперь, согласно формуле надо взять максимальное значение среди всех чисел (-5,2,-3,-3). Это значение равно 2. Итак, мы закончили с анализом левой части уравнения (2.22).

Рассмотрим теперь правую часть уравнения (2.22), т.е. выражение (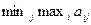). Данное выражение означает, что надо найти максимальное значение чисел по столбцам, а потом выбрать из полученных чисел минимальное значение. Данная процедура выглядит следующим образом. Первый столбец (-5,4,4,2) имеет два максимальных значений числа, равного (4). Второй столбец (3,2,-3,1) имеет максимальное значение числа, равное (3). Третий столбец(-2,3,2,-2) имеет максимальное значение числа, равное (3). Четвертый столбец(-1,2,2,-3) имеет максимальное значение числа, равное (2). Из этих чисел (4,3,3,2) минимальное число соответствует цифре (2). Эта цифра (она соответствует цене игры) стоит на пересечении стратегий ().

Теория игр рекомендует каждому из игроков свою оптимальную стратегию: игрок А должен выбрать стратегию 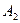, а игрок В должен выбрать стратегию . Любое отклонение от данных стратегий любым из игроков приводит со временем к худшему для них результату.

Однако далеко не всегда получаются матрицы, обладающие седловой точкой. Как быть в таких случаях? Решение данной проблемы появилось в 1928 г., когда фон Нейман доказал фундаментальную теорему теории игр, утверждающую, что любая игра имеет как минимум одно решение, которое может быть найдено в области смешанных стратегий. Понятие «смешанная стратегия» означает, что надо пользоваться не одной стратегией, а с определенной частотой использовать имеющиеся стратегии.

Т.е., в тех случаях, когда матрица такова, что выполнение уравнения () невозможно, решение надо искать в области смешанных стратегий. Последние также дают возможность определить цену игры. Оптимальная стратегия со стороны человека должна заключаться в том, что при любом поведении со стороны противника (природы) выигрыш всегда будет не меньше вычисленной цены игры. Если противник (природа) отклонится от своей оптимальной стратегии, то выигрыш человека может стать больше.

Приведем два примера получения результата в области смешанных стратегий.

Применение теории игр для выбора стратегий в области сельскохозяйственной политики

Предположим, что имеется сельскохозяйственное предприятие, которое выращивает две культуры: . Конечный результат (урожай) зависит от погодных условий. Цель исследования - дать рекомендации, какие культуры и в каких количествах следует сеять, если их урожаи зависят от погоды, а план посева должен обеспечить наибольший доход для сельскохозяйственного предприятия. (Целесообразно иметь в виду, что большая часть России находится в зоне рискованного земледелия).

Проанализируем данную ситуацию с позиции теории игр (Шикин, 2003). Игрок А (человек) имеет четко выраженную цель - получить максимальный урожай. У игрока В (природа) нет явно выраженной цели, но, в зависимости от ситуации, он может сильно навредить игроку А. Итак, у игрока А имеется две стратегии: стратегия 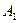- посев первой сельскохозяйственной культуры и стратегия 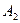- посев второй сельскохозяйственной культуры. У игрока В имеется три стратегии: стратегия - засушливое лето, стратегия - лето с обычным количеством осадков, стратегия - лето с сильно избыточным количеством осадков.

Для решения задачи следует составить матрицу, где указаны расчетные варианты урожаев для сценарных вариантов погодных условий (условно, в млн. рублей).

(2.24)

В полученной матрице отсутствует седловая точка. Поэтому решение задачи надо искать в области смешанных стратегий:

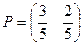(2.25)

Цена игры равна 4.

Физически данное решение означает, что на 60 % территории следует применить стратегию 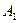(т.е., выращивать первую культуру), а на 40 % территории следует применить стратегию (т.е., выращивать вторую культуру). При этом общий урожай будет не менее 4 млн. рублей (цена игры). Таков результат (урожай) при худших погодных условиях. Если погодные условия будут лучше, то и урожай будет больше.

Дата добавления: 2015-06-26