Производная от функции, заданной неявно

Получаем

.

Произведем следующее преобразование в правой части:

. (30)

Но

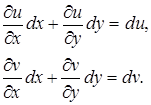(31)

Равенство (30) с учетом равенства (31) можно переписать так:

,

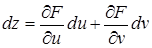или

. (32)

Сравнивая (29) и (32), можем сказать, что выражение полного дифференциала функции нескольких переменных (дифференциала первого порядка) имеет тот же вид, т.е. форма дифференциала инвариантна, являются ли u и v независимыми переменными или функциями независимых переменных.

Пример 23. Найти полный дифференциал сложной функции

z = u ² v ³, u = x ²sin y, v = x ³ e^y.

Решение. По формуле (32) имеем

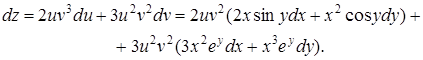
Последнее выражение можно переписать и так:

Задание для самостоятельной работы

Найти частные производные , :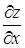

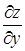56. , , 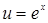.	57. .
58. 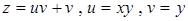.	59. .
60. 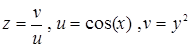.	61. .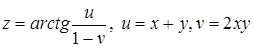

Найти полную производную :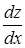

62. 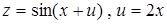.	63. .
64. 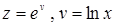.	65. .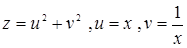
66. .	67. .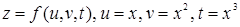

Найти полный дифференциал сложной функции:

68.	69. .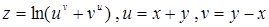
70. z = uv, u = x ^2sin y, v = x ^3 e^y.	71.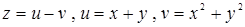
72. .	73.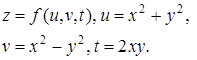

Начнем рассмотрение этого вопроса с неявной функцией одной переменной. Пусть некоторая функция у от х определяется уравнением F (х, у) = 0. Докажем следующую теорему.

Теорема. Пусть непрерывная функция у от х задается неявно уравнением

F (х, у) = 0, (33)

где F (х, у), F ¢ _х (х, у), F ¢ _у (х, у) – непрерывные функции в некоторой области D, содержащей точку (х, у), координаты которой удовлетворяют уравнению (33); кроме того, в этой точке F ¢ _у (х, у) ¹ 0. Тогда функция у от х имеет производную

.

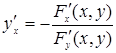Доказательство. Пусть некоторому значению х соответствует значение функции у. При этом F (х, у) = 0. Дадим независимой переменной х приращение D х. Функция у получит приращение D у, т.е. значению аргумента х + D х соответствует значение функции у + D у. В силу уравнения F (х, у) = 0 будем иметь

F (х + D х, у + D у) = 0.

Следовательно,

F (х + D х, у + D у) – F (х, у) = 0.

Левую часть последнего равенства, являющуюся полным приращением функции двух переменных, по формуле (12) можно переписать так

,

где g₁ и g₂ стремятся к нулю при D х и D у, стремящихся к нулю. Так как левая часть последнего выражения равна нулю, можно написать

.

Разделим последнее равенство на D х и вычислим :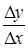

.

Устремим D х к нулю. Тогда, учитывая, что при этом g₁ и g₂ также стремятся к нулю и что 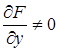, в пределе получим

. (34)

Мы доказали существование производной у ¢ _х от функции, заданной неявно, и нашли формулу для ее вычисления.

Пример 24. Уравнение х ² + у ² – 1 = 0 определяет у как неявную функцию от х. Здесь

, , .

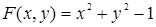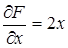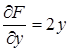Следовательно, по формуле (33)

.

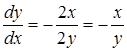Заметим, что заданное уравнение определяет две разные функции (так как каждому значению х в промежутке (-1, 1) соответствует два значения у); однако найденное значение у ¢ _х справедливо как для одной, так и для другой функции.

Пример 25. Дано уравнение, связывающее х и у: 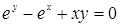. Здесь

, , .

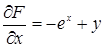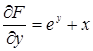Следовательно, по формуле (33) получаем:

.

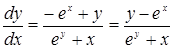Рассмотрим теперь уравнение вида

F (x, y, z) = 0. (35)

Если каждой паре чисел х и у из некоторой области соответствует одно или несколько значений z, удовлетворяющих уравнению (35), то это уравнение неявно определяет одну или несколько однозначных функций z от х и у.

Например, уравнение 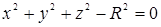неявно определяет две непрерывные функции z от х, у, которые можно выразить явно, разрешив уравнение относительно z; в этом случае мы получаем:

и .

Найдем частные производные 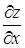и 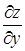неявной функции z от х и у, определяемой уравнением (35).

Когда мы ищем 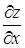, мы считаем у постоянным. Поэтому здесь применима формула (34), если только независимой переменной считать х, а функцией z. Следовательно,

.

Таким же путем находим

.

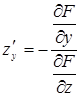Предполагая, что .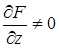

Аналогичным образом определяются неявные функции любого числа переменных и находятся их частные производные.

Пример 26. .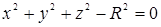

, .

Дифференцируя эту функцию как явную (после разрешения уравнения относительно z), мы получили бы тот же результат.

Пример 27. 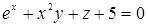. Здесь

.

, , , , .

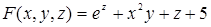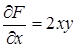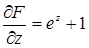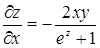Замечание. Все изложенные рассуждения производились в предположении, что уравнение F (х, у) = 0 определяет некоторую функцию одной переменной у = j(х); уравнение F (х, у, z) = 0 определяет некоторую функцию двух переменных z = f (х, у). Укажем без доказательства, какому условию должна удовлетворять функция F (х, у), чтобы уравнение F (х, у) = 0 определяло однозначную функцию у = j(х).

Теорема. Пусть функция F (х, у) непрерывна в окрестности точки (х ₀, у ₀) и имеет там непрерывные частные производные, причем F ¢ _у (х, у) ¹ 0, и пусть F (х ₀, у ₀) = 0. Тогда существует окрестность, содержащая точку (х ₀, у ₀), в которой уравнение F (х, у) = 0 определяет однозначную функцию у = j(х).

Аналогичная теорема имеет место и для условий существования неявной функции, определяемой уравнением F (х, у, z) = 0.

Замечание. При выводе правил дифференцирования неявных функций мы пользовались условиями, которые и определяют существование неявных функций.

Задание для самостоятельной работы

Найти частную производную 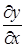при x =1, y =1.

74. 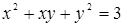.	75. .
76. 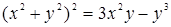.	77. .
78. 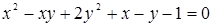.	79. .

Найти частные производные 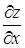и :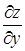

80. .	81. .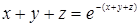
82. .	83. .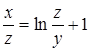
84. 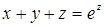.	85. .

Дата добавления: 2015-06-04