Аналитический способ определение равнодействующей системы сходящихся сил

Определение равнодействующей системы сил аналитическим способом

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геоме­трическим способом. Выберем систему координат, определим про­екции всех заданных векторов на эти оси (рис. 3.4а). Складываем проекции всех векторов на оси х и у (рис. 3.46).

Рис.3.4 нижний.

FΣч = Flx + F2x + F3x + F4x; FΣн = Fly + F2y + F3y + F4y;

; .

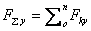Модуль (величину) равнодействующей можно найти по известным проекциям:

.

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействую­щей с осями координат (рис. 3.5).

;

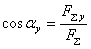
Рис.3.5

Условия равновесия плоской системы сходящихся сил в аналитической форме

Исходя из того, что равнодействующая равна нулю, получим:

FΣ = 0.

Условия равновесия в аналитической форме можно сформулиро­вать следующим образом:

Плоская система сходящихся сил находится в равновесии, ес­ли алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской сходящейся системы сил:

.

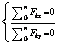13. Теорема о равновесии трёх непароллельных сил.

Закон о трёх силах широко используется при решении задач на равновесие. Покажем переход к нему с помощью ранее описанных методов и опорных фактов.

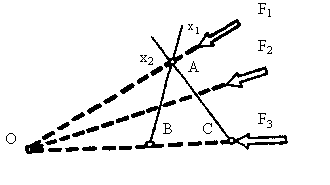
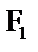
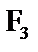
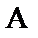
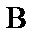
Пусть А (см. рис. 15.14) – произвольная точка на линии действия силы 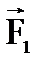. На линии действия силы возьмём две точки - В и С, такие, чтобы и были непараллельными линии действия силы .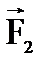

Т.к. тело покоится, а силы 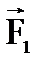и пересекают ось , то из получим: .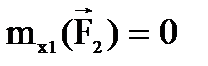

и не || . Остаётся единственное - сила 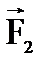также пересекает .

Аналогично рассуждая приходим к выводу: сила 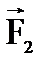пересекает и ось .

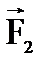пересекает и . Значит она, как и , лежит в плоскости АВС.

Но 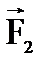и непараллельны. Пусть О - точка их пересечения.

Рассматриваемая система из трёх сил по условию является уравновешенной. Поэтому для неё 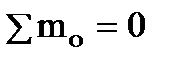. Моменты от сил 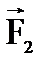и относительно точки О равны нулям. Значит нулю равен и момент относительно точки О силы 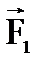. Но 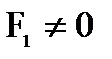. Остаётся единственное: 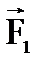также проходит через точку О.

Демонстрация приемлемости применяемых методов перехода от заведомо доверительных (не вызывающих сомнений) механических фактов к другим, завершена.

Дата добавления: 2015-06-04