Понятие о методе максимального правдоподобия

Метод максимального правдоподобия позволяет получать математические модели, характеризующие существенные свойства изучаемых процессов в виде функции правдоподобия (1.8) с оценкой параметра h по результатам экспериментальных измерений показателя Y.

Для этого необходимо:

* Априори установить характер закона распределения значений величины Y.

* Спланировать эксперимент и провести n опытов, в результате которых должна быть получена выборка y₁,..., y_n значений случайной величины Y.

* Определить функцию правдоподобия l{h/ y₁,..., y_n } и оценить параметр h (в общем случае может быть множество параметров q₁,..., q_m).

* На основании полученной оценки h^, или (q₁^,..., q_m^) сделать выводы относительно исследуемого показателя Y.

Пример 1. Предположим, что каждый из m стрелявших из пистолета произвел n выстрелов, стреляя по отдельной мишени. Затем наугад выбрана одна из мишеней. При этом в ней было обнаружено r попаданий. О каждом стрелке нам известно, что он способен попасть в мишень при одном выстреле с вероятностью

p_j , jÎ {1,...,m}.

Необходимо сделать правдоподобное предположение о том, кому из стрелявших вероятнее всего принадлежит выбранная мишень. Очевидно в качестве показателя Y, характеризующего процесс попадания в мишень одним стрелявшим с номером j при n выстрелах, может быть вероятность P_j(^r_n) попасть r раз в мишень для j-го стрелка при n выстрелах. Эта вероятность, как известно, распределена по закону Бернулли:

P(r,n, p_j) = C^r_n p^r_j(1-p_j)^n-r. (1.9)

Параметр p^_j, максимизирующий вероятность P(r, n, p_j), позволяет сделать вывод о том, что выбранная мишень с r пробоинами с наибольшей вероятностью принадлежит стрелявшему под номером j, который имеет способность (вероятность) p_j попадать в мишень при одном выстреле наиболее близкую к оценке p^_j. Для оценки p^_j составляем функцию правдоподобия

l{p_j, r, n}=p^r_j(1-p_j)^n-r. Данная функция достигает максимума при p^_j = r/n [15]. Следовательно, наиболее вероятно, что выбранная мишень принадлежит стрелявшему под номером j, соответствующему оценке p^_j=r/n.

Пример 2. Предположим, что задача состоит в том, чтобы оценить вес некоторого предмета посредством взвешивания его на n различных весах приблизительно одинаковой точности. В результате получается выборка у₁, y₂,..., y_n значений оцениваемого показателя Y, характеризующего вес данного предмета. Y является случайной величиной, распределенной по нормальному закону:

(1.10)

где h - математическое ожидание величины Y, а s² - дисперсия этой величины. Так как по определению s² характеризует разброс значений y_i относительно математического ожидания h, то величина s² не влияет на положение максимума параметра h. Поэтому для упрощения вычислений можно положить s² = 1. Тогда выражение (1.10) приобретает вид:

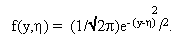
Отсюда формула правдоподобия параметра h имеет вид:

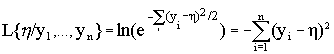(1.11)

(При определении функции правдоподобия постоянные коэффициенты можно опустить) Функция (1.11) достигает максимума при таком значении h, для которого сумма

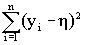принимает минимальное значение. Этот факт был использован для разработки широко известного метода оценки параметров математической модели изучаемого процесса, называемого “ методом наименьших квадратов ”.

При исследовании сложных систем показатель Y изучаемого свойства может быть функцией от многих факторов x₁,..., x_n и представлять собой случайную функцию Y = f(x₁,..., x_n, q₁,..., q_m). Задача исследователя состоит в том, чтобы с помощью эксперимента определить такую функцию h(X, Q) c параметрами q₁,..., q_m, которая с наибольшей вероятностью соответствует реальной функции Y. Согласно принципу максимального правдоподобия полагают, что функция h(X, Q) должна представлять собой множество значений {E(y_i)}, где E(y_i) - математическое ожидание случайной величины Y в точке X_i (X_i - набор значений факторов x₁,..., x_n в точке i).

Функция h(X, Q) обычно представляется в виде линейного относительно параметров q₁,... q_m полинома

h (X,Q) = q ₀f₀(X) + q ₁f₁(X) +... + q _mf_m(X), (1.12)

который называется уравнением регрессии случайной величины Y. В случае однофакторной функции Y ее уравнение регрессии может быть представлено в виде разложения в ряд Фурье:

h (x, Q) = q ₀ ¹/₂ + q ₁ Sin (x) + q ₂ Cos (x) +...,

или в виде разложение в ряд Тейлора:

h (x,Q) = q ₀ + q ₁x + q ₂x² +....

В данном случае функция h (х, Q) называется линией регрессии. Когда функция U является многофакторной, применяется разложение в форме полинома (1.12), где f_i(x) представляет собой комбинацию из n по r факторов x_iI {x₁,..., x_n}. В этом случае число членов в разложении полинома определяется величиной

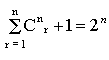, а уравнение регрессии, представленное таким полиномом имеет следующий вид:

h (C, Q) = q ₀(x⁰₁ x⁰₂ ... x⁰_n) + q ₁(x¹₁ x⁰₂ ... x⁰_n) +... + q ₂^n-1(x¹₁... x¹_n). (1.13)

Поэтому проблема состоит еще и в том, как выбирать полином (1.12) так, чтобы трудоемкость вычислений была бы по возможности наименьшей. Эта проблема называется планированием эксперимента. Для того чтобы полиномиальное представление функции h (C, Q) было хорошо обозримым и удобным для вычислений, введем следующие обозначения:

X^Kj = (x_1a ¹,..., x_na ⁿ)_j,

где a _eI {0, 1}=A_e, e = 1,...,n, (a ₁,...,a _n)_j= K_jI {A_1? ...? A_n}. Другими словами, K_j - есть двоичное число от (0₁, 0₂,..., 0_n) до (1₁,1₂,..., 1_n). В силу данных обозначений X^Kj представляет (обозначает) вполне определенную комбинацию переменных x₁,..., x_n, например, при K_j = (1₁, 0₂,..., 0_n) X^Kj= x₁, при K_j = (1₁, 1₂, 0₃,..., 0_n) X^Kj = x₁ x₂ , и так далее. При этом полином (1.13) может быть записан в следующем виде:

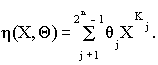Данное представление позволяет включать в полином только некоторое ограниченное количество членов, обеспечивающее заданную точность. Это может быть использовано для построения эффективных алгоритмов планирования экспериментов и вычисления параметров q ₀,...,q _n. Если случайная величина Y распределена по нормальному закону, то имеет место следующее уравнение:

из которого логарифмическая функция правдоподобия выборки y₁,..., y_s случайной величины Y получается в виде:

Чтобы найти значения функции h (C _{i, Q )} , максимизирующие данную функцию правдоподобия в точках X_i, необходимо решить систему следующих дифференциальных уравнений:

¶ L{h (C _{1, Q ) ,} y₁,..., y_s} / ¶ q _j = 0, j = 1,...,m.

В общем случае эта система имеет следующий вид:

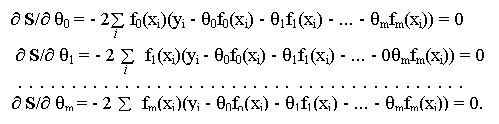(1.14)

В результате решения данной системы линейных уравнений получают множество оценок q ^{^}₀, q ^{^}₁,..., q ^{^}_m параметров q ₀, q ₁,..., q _m искомой функции h (C _{i, Q )} . Для решения этой системы обычно применяют матричную алгебру. Система уравнений (1.14) может быть получена и другим способом. Данный способ основан на предположении, что каждое значение y_i получается из опыта с некоторой погрешностью x _i. При этом имеет место система уравнений

x _i = y_i - h (C _{i, Q )} , i = 1,...,s.

Степень приближения функции h (C _{i, Q )} к экспериментальным данным

оценивается величиной дисперсии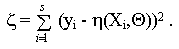

Таким образом, приходят к соотношению | S| = z, показывающему, что оценки параметров q _j логарифмической функции правдоподобия S и дисперсии z имеют одинаковые значения в точке экстремума. Заметим, что данный способ не предполагает никаких ограничений на вид распределения случайной величины Y. Поэтому можно считать, что функция S (z) годится для оценки параметров функции регрессии h (C _i,Q) случайной величины Y при любом законе ее распределения.

Дата добавления: 2015-06-04