Кинематика

Запредельное торможение

Этот вид торможения отличается от внешнего и внутреннего по механизму возникновения и физиологическому значению. Оно возникает при чрезмерном увеличении силы или продолжительности действия условного раздражителя, вследствие того, что сила раздражителя превышает работоспособность корковых клеток. Это торможение имеет охранительное значение, так как препятствует истощению нервных клеток. По своему механизму оно напоминает явление "пессимума", которое было описано Н.Е.Введенским.

Запредельное торможение может вызываться действием не только очень сильного раздражителя, но и действием небольшого по силе, но длительного и однообразного по характеру раздражения. Это раздражение, постоянно действуя на одни и те же корковые элементы, приводит их к истощению, а следовательно, сопровождается возникновением охранительного торможения. Запредельное торможение легче развивается при снижении работоспособности, например, после тяжелого инфекционного заболевания, стресса, чаще развивается у пожилых людей.

1 Нүкте қозғалысының векторлық тәсілмен берілуі?

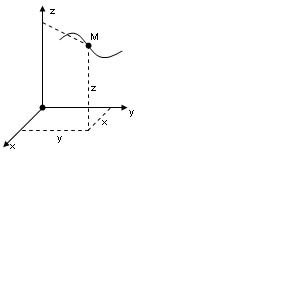
Бұл тәсілде Оxyz координаттар жүйесіне қатысты нүктенің орны R=OM векторымен анықталады.Координаттар бас нүктесін және берілген М нүктесін қосатын вектор r ді нүктенің радиус векторы деп атайды. Қозғалыс кезінде r өзінің модулін де бағытын да өзгертеді. Демек ол е t-ның бір мәнді, үздіксіз, дифференциалданатын функциясы болып келеді. r=r(t) өрнегі нүкте қозғалысының векторлық теңдеуі.

1,2Қозғалу траекториясы?

Қозғалу траекториясы дегніміз- дененің жүріп өткен жолының бастапқы және соңғы нүктесін қосатын кесіндіні айтамыз.

1,3Нүктенің жылдамдық және үдеу векторлары

V=dr/dt Берілген сәттегі нүкте жылдамдығы деп, оның радиус векторының уақыт бойынша алынған туындысына тең болып келген векторлық шама, v ны айтамыз.

Қозғалысы вектормен берілген нүкте жылд нүкте М нің қозғаласы Oxyz коорд жүйесі R тең болады R(t) теңдеуімен анықталатын R вектор өсімшесі t ға қатынасы t уақыт аралығындағы нүктенің орша жылдамдығы.

Жылдамдықтың уақыт өтуіне байланысты өзгеруінің тездігін сипаттаушы физикалық шаманы үдеу деп атайды.Берілген уақыт мезетіндегі нүктенің үдеуі деп жылдамдық векторының уақыт бойынша алынған бірінші туындысына a=dv/dt немесе нүктенің радиус-векторының уақыт бойынша алынған екінші туындысына a=d2r/dt2 тең болатын векторлық шаманы айтамыз.

Лездік үдеу векторы а, траекторияның М нүктесіндегі жанаспа жазықтығында жатады және М нүктесінен траекторияның ойыс жағына қарай бағытталады.

2 Нүктенің X,Y,Z уақыт t ның үздіксіз бірмәнді функциялары болып келсе яғни; x=f(t) Y=f(t) Z=f(t)(2.2) онда нүктенің әрбір уақыт сәтіндегі орны толық анықталады

Сонымен, нүктенің орнын анықтаудың координаттар тәсіліне қандай да бір координаттар жүйесінде оның координаттары уақытқа тәуелді функция ретінде беріледі.(2.2) теңдеулер нүкте қозңалысының теңдеулері деп аталады.

Сонымен қатар бұл теңдеулерге нүкте траекториясының параметрлік теңдеулері деп қарауға болады.Траектория теңдеуін нықтау үшін (2.2) теңдеулерден параметр рөлінде тұрған t-ны алып тастау керек. Сонда траекторияның теңдеуін мынадай екі теңдеу жүйесі түрінде аламыз

F1(x,z)=0 F2(y,z)=0

Егер нүкте бір жазықтықта қозғалатын болса онда оның қозғалысы екі скаляр теңдеулемен беріледі; X=f1(t) Y=f2(t)7

Қозғалысы координаттық тәсілде берілген нүкте жылдамдығын анықтау;

Нүктенің Oxyz санақ жүйесіндегі қозғалысы координаттық тәсілде берілген.Демек нүктенің осы санақ жүйесіндегі координаттары x,y,z уақытұа тәуелді функциялар түрінде берілген

x=f(t) y=f(t) z=f(t) (2.15)

Қозғалыс теңдеулері (2.15) арқылы берілген М нүктесінің жылдамдығын анықтауға қажетті формулаларды табуымыз керек. Осы мақсатпен жоғарыда көрсетілген

V=dr/dt (2.16)

векторлық теңдеуіндегі r=OM радиус векторын оның Oxyz остеріндегі құраушылары арқылы өрнектейік.

r=xi+yj+zk (2.17)

(2.17) өрнегін (2.16) теңдіктегі орнына қояйық

v=d(xi+yj+zk)/dt (2.18)

Осыдан

V 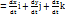(2.19)

Енді жылдамдық векторы v ны үш құраушыға жіктеп оны (2.19) теңдігінің сол жағына қоямыз

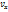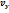i+ j+ 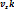= 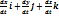(2.20)

(2.20)тепе теңдігіндегі өзара тәуелсіз i, j, k векторының алдындағы коэффициенттерді теңестіреміз

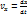
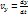
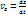(2.21)

(2.21) формулалары нүкте жылдамдығы v ның координатттық остердегі проекцияларын орнектейді. Жылдамдық проекциялары (2.21) табылғаннан кейін вектордың өзі де толық табылады. Оның модулі мына формуламен анықталады.

v= 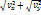+ 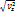(2.22)

Осыдан соң жылдамдық векторының бағыттаушы косинустарын есептей аламыз

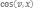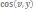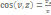= = (2.23)

Қозғалысы координаттық тәсілде берілген нүкте үдеуі

Қозғалмайтын Oxyz координаттар жүйесіндегі нүкте қозғалысы

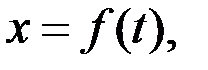
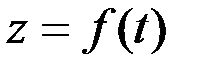(2.24)

теңдеулерімен анықталады дейік. Осы теңдеулер арқылы нүкте үдеуін қалай есептеуге болатынын көрейік. Нүкте үдеуі деп (2.13) не (2.14) векторлық теңдікпен берілген векторды айтамыз. (2.14) теңдіктің оң жағындағы радиус-вектор 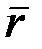-ді координаттар өстеріне жіктеп жазуға болады:

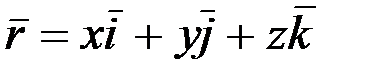. (2.25)

(2.25)-тегі 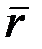векторының компоненттерін (2.14) теңдігіне қойып

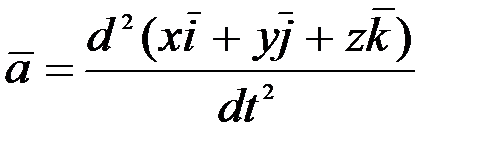. (2.26)

(2.26) теңдігінің оң жағындағы туындыны есептеп шықсақ, мына теңдікке келеміз:

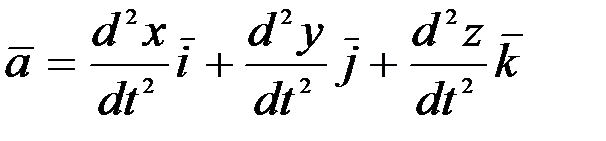. (2.27)

Енді үдеу векторы -ны үш құраушыға жіктеп оны (2.27) теңдігінің сол жағына қоямыз:

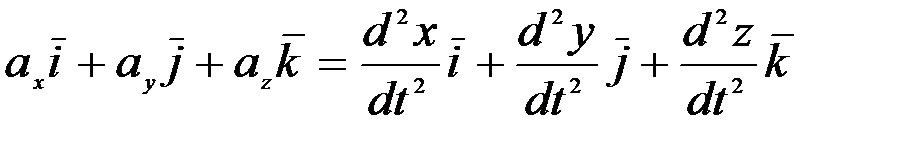. (2.28)

(2.28) теңдігі орынды болуы үшін, бұл теңдіктің екі жағында тұрған өзара тәуелсіз 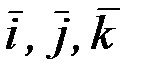бірлік векторларының әрбіреуінің араларындағы коэффициенттері бірі-біріне тең болуы керек:

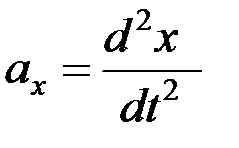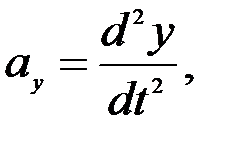
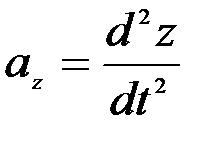, . (2.29)

Үдеу модулі мына формуламен анықталады:

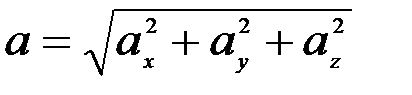. (2.30)

Үдеу векторының кеңістіктегі бағыты оның бағыттаушы косинустарымен анықталады:

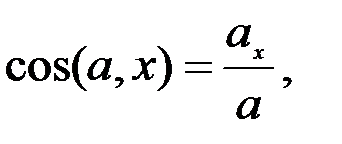
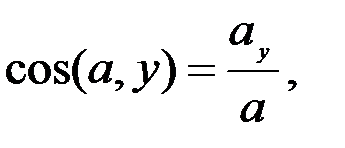
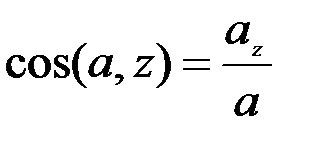. (2.31)

3 Нүкте қозғалысының табиғи тәсілмен берілуі

Нүкте қозғалысының берілуінің табиғи тәсілінде нүктенің кез келген бір санақ жүйесіне қатысты траекториясы беріледі. Одан кейін, оның бойынан қандайда болсын бір нүкте О ₁-ді доға ұзындығын есептеудің бастапқы нүктесі етіп алып, қашықтықты санаудың оң бағыты үшін мүмкін екі бағыттың кез келген бірі алынады. Сонда М нүктесінің орны S=O₁M шамасымен анықталады.

А нүктенің траектория бойындағы орнын әрбір уақыт сәтінде де таба алуымыз үшін, доға ұзындығы S=O₁M және уақыт t- ның әрбір мәніне сәйкес келетін S -тің мәнін беретін бір сарынды, үздіксіз уақыт функциясы берілуі керек.

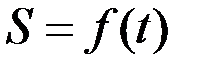(2.1)

2.2-сурет  

Доға ұзындығы S пен уақыт t-ның арасындағы функциялық тәуелділік (2.1) нүктенің траектория бойымен қозғалуы-ның заңы деп аталады.

3,1 Табиғи үш жақ

2.9-сурет  

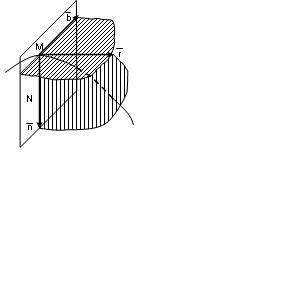1. Табиғи үш жақ. Табиғи өстер. Траекторияның бір–біріне шексіз жақын орналасқан үш нүктесі арқылы өтетін жа-зықтық, оның ортаңғы нүктесіне жүргізі-лген, жанаспа жазықтық деп аталады.

Жанамаға перпендикуляр, М нүктесі арқылы өтетін, N-жазықтығы траекто-рияның осы нүктедегі нормаль жазықтығы деп аталады.

Траекторияның М нүктесіндегі жанама арқылы өтетін нормаль және жанаспа жазықтықтарға перпендикуляр үшінші жазықтық траекторияның сол нүктедегі түзулеуші жазықтығы деп аталады (2.9-сурет). Жанаспа жазықтықта жатқан нормаль қисықтың М нүктесіндегі бас нормаль деп, ал жанаспа жазықтыққа осы нүктеде жүргізілген перпендикуляр бинормаль деп аталады. Жанаманың оң бағыты (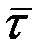 бірлік векторы) қозғалыспен бағыттас келеді. Бас нормальдың оң бағыты ( 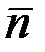бірлік векторы) траекторияның ойыс жағына қарай бағыт-талады. Бинормальдың оң бағыты ( 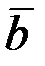бірлік векторы) 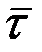және 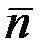векторларымен оң координаттар жүйесін құрайтындай етіп алынады. 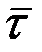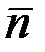Бас нүктесі М болатын бұл координаттар жүйесі М 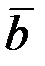табиғи координаттар жүйесі деп немесе табиғи үшжақ деп аталады. Координаттар жазықтары екі-екіден алынған бірлік векторларымен анықталады. (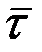, 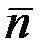) –жанаспа жазықтық, (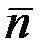, 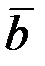) – нормаль жазықтық, (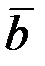, 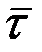) – түзулеуші жазықтық.

4 Нүкте қозғалысының кейбір жеке түрлері

Траекторияның түріне қарай нүкте қозғалысы екі топқа бөлінеді. Қозғалыс кезінде түзу сызық сызатын нүктені түзу сызықты қозғалыс жасайды дейміз, траекториясы қисық сызық түрінде болып келетін нүктені екінші топқа жатқызамыз. Нүкте жылдамдығының өзгеруіне қарап бұл екі топтағы нүкте қозғалыстарының әрқайсысын әр түрге бөліп атаймыз. Алдымен нүктенің түзу сызықты қозғалысына жеке тоқтап өтейік.

1. Түзу сызықты бірқалыпты қозғалыс. Түзудің қисықтық радиусы 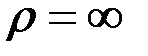болғандықтан түзу сызықты қозғалыстағы нүктенің нормаль үдеуі нөлге тең болады да, оның толық үдеуі жанама құраушысына тең болады:

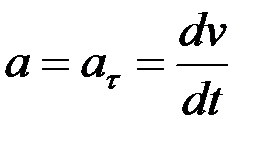. (2.50)

Нүктенің жылдамдығы тұрақты, түзу сызықты қозғалысы – түзу сызықты бірқалыпты қозғалыс деп аталады. Мұндай қозғалыстың (2.50) – формула бойынша үдеуі нөлге тең болады да, қозғалыс кезіндегі уақыттардың бәрінде жылдамдық векторы модулін өзгертпей сақтайды.

Түзу сызықты, бірқалыпты қозғалысты сипаттайтын формулалар мынадай:

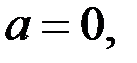
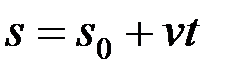. (2.51)

2. Түзу сызықты бірқалыпты айнымалы қозғалыс. Үдеуі тұрақты нүктенің түзу сызықты қозғалысы – бірқалыпты айнымалы қозғалысы деп аталады, мұндай қозғалысты сипаттайтын формулалар элементар физикадан белгілі:

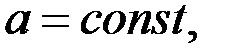
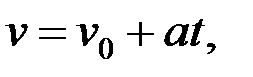
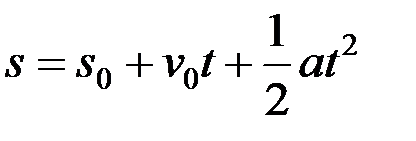
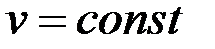. (2.52)

3. Қисық сызықты бірқалыпты қозғалыс. Нүктенің қисық сызықты қозғалысында болса, онда ол бірқалыпты қисық сызықты қозғалыс деп аталады. Демек, бірқалыпты қисық сызықты қозғалыс кезінде нүктенің жанама үдеуі нөлге тең болады да, толық үдеуі өзінің нормаль құраушысына тең болып келеді. Қисық сызықты бірқалыпты қозғалысты сипаттайтын формулалар мына түрде жазылады:

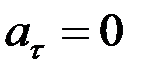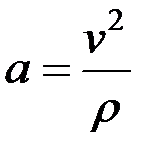, . (2.53)

Нүкте жылдамдығын өрнектейтін теңдеуді интегралдау арқылы бірқалыпты қисық сызықты қозғалыс заңын табамыз:

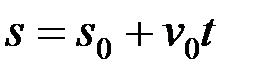. (2.54)

4. Қисық сызықты бірқалыпты айнымалы қозғалыс. Нүктенің жанама үдеуі қозғалыс кезінде үнемі тұрақты, яғни

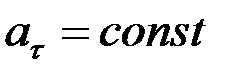, (2.50)

болса, онда қисық сызықты қозғалыс бірқалыпты айнымалы қозғалыс деп аталады. Мына теңдікті түрлендіре отырып оны мына түрде жазайық:

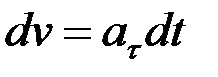. (2.55)

Осы теңдеуді интегралдау арқылы қозғалыс жылдамдығының өзгеру заңын табамыз:

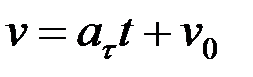, (2.56)

мұндағы, ν ₀ нүктенің t₀=0 болған кездегі бастапқы жылдамдығы. Қисық сызықты бірқалыпты айнымалы қозғалыс заңын

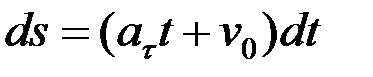. (2.57)

теңдеуін интегралдау арқылы мына түрде аламыз:

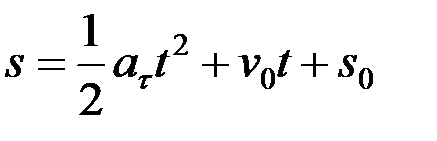, (2.58)

мұндағы, 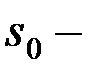бастапқы қашықтық.

4. Қисық сызықты қозғалыстың жалпы жағдайы. Үдеу векторы жылдамдық векторының өзгеру тездігін анықтайды. Ол жалпы жағдайда жанама және нормаль құраушыларға жіктеледі. Жанама үдеу жылдамдық векторының сан мәнінің өзгеруін, ал нормаль үдеу жылдамдық бағытының өзгеруін сипаттайды. Жалпы жағдайда, жылдамдықтың өзгеруі толығынан қарастырылатындықтан 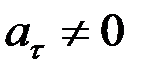, 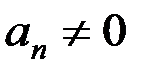болып келеді.

Жалпы жағдайдағы қисық сызықты қозғалыс үдемелі және кемімелі деген екі түрге бөлінеді. Үдемелі қозғалыс кезінд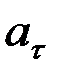е және шамаларының таңбалары бірдей, ал кемімелі қозғалыс кезінде бұлардың таңбалары қарама-қарсы болып келеді. Басқаша айтқанда, үдемелі қозғалыс кезінде жанама үдеу векторы жылдамдық векторымен бірдей бір жаққа қарай бағытталады, ал кемімелі қозғалыс кезінде ол жылдамдық векторына қарама-қарсы бағытта болады. 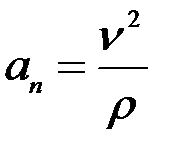оң шама болғандықтан нормаль үдеу бас нормальмен бірдей бағытталады. Нормаль үдеу траекторияның қисықтық центріне қарай бағытталуына байланысты, ол кейде центрге ұмтылғыш үдеу деп те аталынады. Осыдан, бұрын айтылған үдеу векторының үнемі траекторияның ойыс жағына қарай бағытталатындығын, нормаль үдеу туралы берілген осы түсінік, оны айқындай түседі.

5 Қатты дeнeнің ілгерілeмeлі қозғалысы

Қатты дененің ілгерілемелі қозғалысы деп оның әрбір екі нүктесін қосатын түзулердің кез келген өзіне-өзі тек параллель қозғалатындай қозғалыс түрін айтамыз. Демек ілгерілемелі қозғалыстағы дене бойынан алған кез келген түзу өзінің бастапқы бағытын өзгертпей сақтайды.

Қозғалмайтын О₁ξηζ өстер жүйесіне қатысты ілгерілемелі қозғалыс жасайтын қатты дене Д берілсін. Оның кез келген бір нүктесі О -ны полюс ретінде қабылдап, денеге өзгерместей етіп бекітілген қозғалмалы координаттар жүйесін алайық.

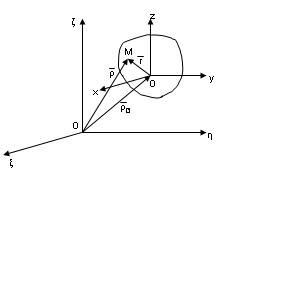
2.14-сурет  

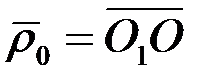Бұл қозғалмалы жүйенің өстерін негізгі жүйе өстеріне параллель бағыттаймыз (2.14-сурет). Таңдап алынған О -бас нүктенің қозғалмайтын О₁ξηζ жүйесімен салыстырғандағы кеңістіктегі орны радиус-векторымен, ал дененің кез келген М нүктесінің қозғалмалы Oxyz жүйесімен салыстырғандағы орны 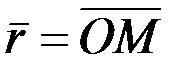радиус – векторымен анықталады. Дене абсолют қатты және тек қана ілгерілемелі қозғалыста бол-ғандықтан 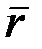радиус-вектор шамасы жағынан да, бағыты жағынан да тұрақты болады, яғни оның осы координаттар өстеріне проекциялары а, в, с тұрақты сандар болады. Суреттегі О₁ОМ векторлық үшбұрыштан, М нүктесінің О₁ξηζ жүйесіндегі орнын анықтайтын радиус-вектор 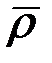-ның өрнегін табамыз:

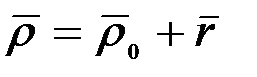(2.59)

мұндағы, 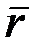= const.

Әртүрлі уақыт мезгіліндегі сәйкес нүктелерінің арасын қосатын кесінділер, мысалы ОМ кесіндісі, өзара параллель және тең болатын қисықтар (траекториялар) эквидистанттық немесе конгруэнтті қисықтар (траекториялар) деп аталады. Ілгерілемелі қозғалыстағы дене нүктелерінің траекториялары кез келген эквидистанттық қисық сызықтар болады.

Дененің (2.43) қозғалыс теңдеуінің екі жағынан да уақыт бойынша туынды аламыз. Сонда:

,

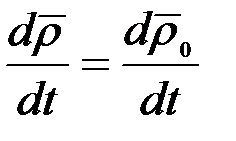немесе:

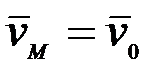(2.60)

яғни, ілгерілемелі қозғалыстағы қатты дененің барлық нүктелерінің берілген бір уақыт мезгіліндегі жылдамдықтары өзара тең болады.

Қатты дененің ілгерілемелі қозғалысын кез келген уақыт мезгілінде дененің барлық нүктелерінің жылдамдықтары өзара тең болатын қозғалыс деп те атайды. Мұндай қозғалысты пермаменттік (тұрақты) ілгерілемелі қозғалыс деп атаймыз.

Дененің үдеу векторларының орналасуын анықтау үшін (2.60) –теңдіктен уақыт бойынша туынды ала аламыз:

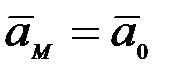
яғни, пермаменттік ілгерілемелі қозғалыстағы қатты дененің барлық нүктелерінің кез келген уақыт мезгіліндегі үдеулері өзара тең.

Сонымен, пермаменттік ілгерілемелі қозғалыстағы қатты дененің барлық нүктелерінің кез келген уақыт мезгіліндегі сәйкес кинематикалық сипаттамалары бірдей, яғни олардың біреуінің ғана мысалы О нүктесінің қозғалысын зерттеп білсек болғаны.

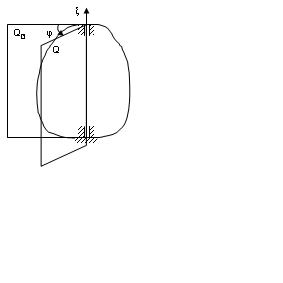
6 Қатты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысы

Қозғалмайтын өсті айнала қозғалатын дене деп, екі нүктесі қозғалмайтын денені айтамыз. Қозғалмайтын нүктелерді қосатын түзу оның айналу өсі болады.

Қозғалмайтын Q_о және Q жазықтықтарының арасындағы екі жақты бұрыш φ қатты дененің айналу бұрышы деп аталады. Бұл бұрыш берілген дененің кез келген уақыт мезгіліндегі орнын бірмәнді анықтайды. Демек, қозғалмайтын өсті айналатын қатты дененің бір ғана еркіндік дәрежесі болады. Дененің қозғалмайтын өс төңірегіндегі орны бір параметрмен анықталады. Мұндай параметр рµлін φ бұрышы атқарады. Ол уақыттың бірмәнді функциясы болып келеді.

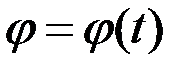. (2.61)

Бұл (2.61) теңдеуі қатты дененің айналу заңы немесе айналу теңдеуі деп аталады.

Айналу бұрышы 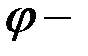дің таңбасын анықтауда оң бұранда ережесіне сүйенеміз. Егер 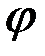бұрышы айналу өсі 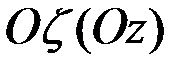-оң ұшынан қарағанда қозғал-майтын Q ₀ жарты жазықтықтан Q жарты жазықтыққа қарай сағат тілінің қозғалысына қарсы бағытта сана-латын болса, айналу бұрышын оң таңбалы деп санаймыз. Ал егер ол кері бағытпен анықталса, оны “–” таңбамен алуымыз керек. Айналу бұрышы үнемі радианмен өлшенеді.

Дененің қозғалмайтын өсті айналуын сипаттауға қажетті екінші бір кинематикалық шаманы бұрыштық жылдамдық деп атайды. Оның алгебралық шамасы ω әрпімен белгіленеді. Бұрыштық жылдамдық ω дененің айналу бұрышы φ -дің уақыттың өтуіне қарай өзгеру тездігін белгілейтін шама. Алдымен белгілі бір уақыт аралығына сәйкес келетін айналу бұрышының өзгеруін қарастырайық. Егер оның t уақытына сәйкес мәні φ(t) –болсын, ал уақыттың t₁ =t+Δt мезгіліндегі мәні φ(t+Δt) болсын. Демек Δ t уақыт аралығында дене Δ φ бұрышына айналыс жасайды:

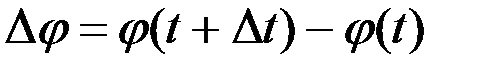(2.62)

осындағы айналу бұрышының өсімшесі (2.62)-нің оған сәйкес келетін уақыт өсімшесі Δ t -ға қатынасын құрайық та, оны ω_орт деп белгілейік:

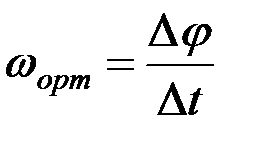. (2.63)

ω_орт орташа бұрыштық жылдамдығы деп атайды. (2.63)-тің екі жағында Δt→0 кездегі шегі:

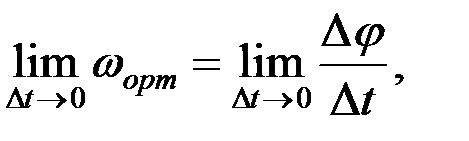
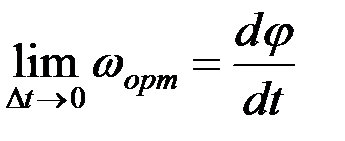. (2.64)

(2.64)-тің оң жағындағы шек φ(t) функциясының туындысын береді.

Ал оның сол жағындағы шек дененің берілген t уақыт мезгіліндегі бұрыштық жылдамдығы ω -ны береді. Осы түсіндір-мелерді қабылдап (2.64) теңдігін мына түрде жазамыз:

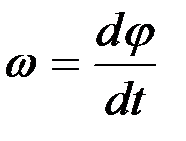. (2.65)

Бұрыштық жылдамдық векторлық шама. 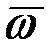– векторы дененің айналу өсінің бойында орналасып, оң бұранда ережесіне сәйкес келетін бағытпен бағытталады.

Жоғарыда айтылған φ бұрышын санаудың оң бағыты жөніндегі анықтаманы ескере отырып, бұрыштық жылдамдық векторын мынадай формуламен өрнектеуге болады:

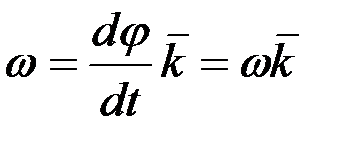, (2.66)

мұндағы 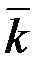, 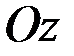өсінің бірлік векторы.

2.15-сурет

Дененің айналмалы қозғалысын сипаттаушы үшінші кинема-тикалық шама, бұрыштық үдеу ұғымына тоқтап өтейік. Алдымен орташа бұрыштық үдеуді анықтаймыз. Берілген t уақыт мезгіліндегі айналмалы қозғалыстың бұрыштық жылдамдығы ω(t) болсын, ал t +Δ t уақыт мезгілінде ол ω(t +Δ t) болсын дейік. Сонда Δ t уақыт аралығында бұрыштық жылдамдық өсімшесі мынаған тең болады:

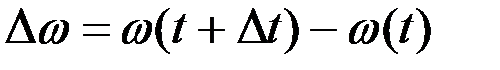. (2.67)

Осы шамалар қатынасын дененің Δt уақыты аралығындағы орташа бұрыштық үдеу деп атап, оны ε_орт әрпімен белгілейміз:

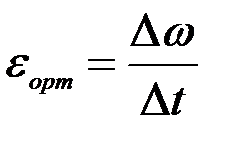. (2.68)

Бұл қатынасты пайдалана отырып, дененің берілген уақыт t мез-гіліндегі, яғни лездік бұрыштық үдеудің анықтамасын бере аламыз.

Берілген уақыттағы бұрыштық үдеу деп орташа бұрыштық үдеудің Δt →0 кездегі үдеудің шегін айтамыз. Бұрыштық үдеуді ε -деп белгілесек, айтылған анықтама мына формуламен беріледі:

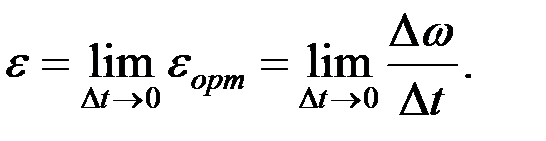(2.69)

(2.69) –теңдіктің оң жағында ω(t) функциясының уақыт бойынша алынған туындысы тұрғанын ескерсек, оны мына түрде қайталап жаза аламыз:

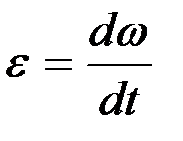немесе 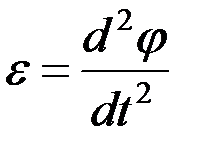. (2.70)

Бұрыштық үдеу бұрыштық жылдамдықтан уақыт бойынша алынған бірінші туындыға тең немесе φ айналу бұрышынан уақыт бойынша алынған екінші туындыға тең болатын шама. Бұрыштық үдеу векторы 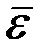де айналу өсінің бойында орналасады. Бұрыштық үдеу векторын мынадай формуламен өрнектеуге болады:

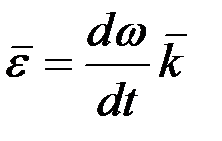немесе 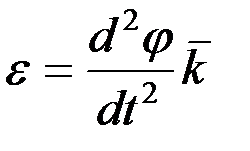. (2.71)

Бір қалыпты айналмалы және бір қалыпты айнымалы айналмалы қозғалыстар. Егер қозғалыс кезінде бұрыштық үдеу ε =0 болса, онда қозғалыс ω =const тұрақты бұрыштық жылдамдықпен орындалады. Мұндай қозғалысты бір қалыпты айналмалы қозғалыс деп атаймыз. Осындай қозғалыстың бұрыштық жылдамдығының анықтамасынан мынадай өрнек алынады:

.

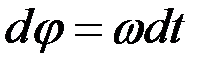Егер t ₀ = 0 болғанда φ = φ ₀ десек, соңғы теңдіктен мынадай формула шығады:

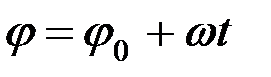. (2.72)

мұндағы бастапқы φ ₀ = 0 болып келген жағдайда (2.72) –теңдіктен:

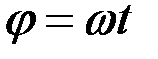және 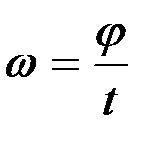. (2.73)

Дененің айналысы кезінде оның бұрыштық үдеуі ε т±рақты болатын болса, онда мұндай айналмалы қозғалысты бір қалыпты айнымалы дейміз.

Бұрыштық үдеу анықтамасынан:

.

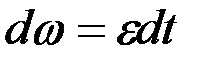Бұл теңдікті сәйкес алынған шектерде (t ₀=0 саналады) интег-ралдау арқылы, мынадай формула аламыз:

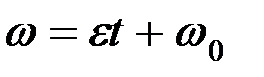. (2.74)

Бұл формуламен ε =const болған жағдайдағы бұрыштық жылдамдық анықталады. (2.74) –тің екі жағында dt -ға көбейтіп интегралдау арқылы мынадай формула аламыз:

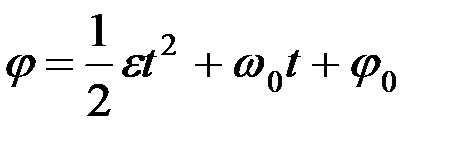. (2.75)

7. Қатты дeнeнің жазық параллeль қозғалысының заңы, оның анықталу тәсілдeрі

Егер қатты дененің барлық нүктелері қандайда бір қозғал-майтын жазықтыққа параллель қозғалатын болса, онда дененің мұндай қозғалысын жазық – параллель қозғалыс дейміз (2.20-сурет). Қозғалмайтын жазықтық-ты (ж)-деп белгілейік. Дененің О нүктесі арқылы (ж) жазық-тығына параллель етіп (ж) жазықтығы дененің (S) қимасын береді.

Бұл (S) – қиманың барлық нүктелерінің негізгі (ж) – жа-зықтығынан қашықтықтары қоз-ғалыс кезінде өзгермейді, тұрақты болады. Демек, (S) – қимасы үнемі (ж) – жазықтығында жатады және ол өзінің пішінін өзгертпейді.

2.20-сурет  

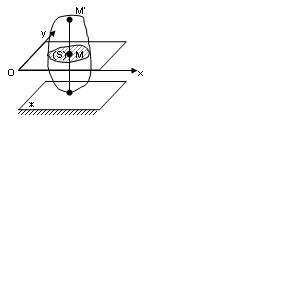
Сөйтіп, қатты дененің жазық – параллель қозғалысын зерттеу оның қозғалмайтын жазықтыққа параллель қималарының бірінің мысалы (S) –тің, жататын (ж) – жазықтықтың бетімен қозғалуын зерттеуге келтіріледі. Қозғалмайтын Ωξηζ және жазық фигура (S) –ке қатаң бекітілген Oxyz координаттар жүйеле-рін таңдап алайық (2.21-сурет).

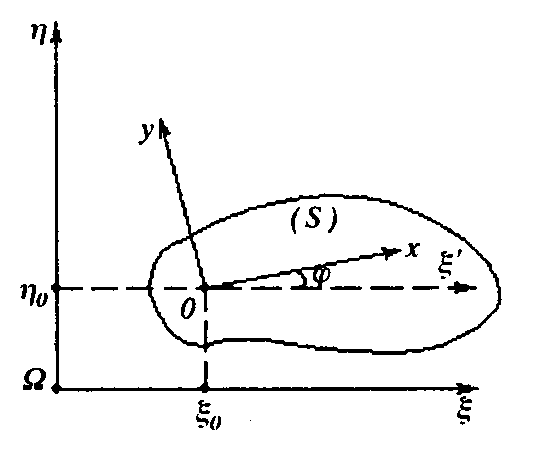
2.21-сурет

Қозғалмалы Oxyz координаттар жүйесінің бас нүктесі О- ны бұдан былай «полюс»-дейміз.

Полюс О -ның өстеріне қатысты координаттарын ξ ₀ және η ₀ деп бел-гілейік. Сонда, мына теңдеулер:

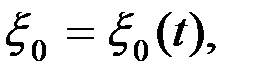
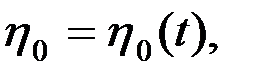
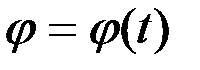(2.89)

жазық фигураның қозғалмайтын Ωξη координаттар жазықтығындағы қозғалысын анықтайды. Демек, бұлар жазық фигураның өз жазықтығындағы қозғалысының, күрделі қозғалыс екенін көрсетеді. Оны негізгі екі қүрауышы қозғалысқа жіктеуге болады. Олардың біреуі, жылдамдығы полюс жылдамдығына тең, ілгерілемелі қозғалыс, ал екіншісі, қозғалмайтын центр ретінде қарастырылатын полюс О арқылы өтіп, жазық фигура жазықтығына перпендикуляр орналасатын лездік өс жанындағы, лездік айналыс.

8. Қ.д жазық параллель қозғалысы. Қатты денелердің барлық нүктелері қандай да бір қозғалмайтын жазықтықка параллель қозғалатын болса,онда дененің мұндай қозғалысын жазық параллель қозғалыс дейміз. Жазық фигураның кез келген нүктесінің жылдамдығы полюс жылдымдығымен осы нүктенің полюске қатысты алынған жылдымдығының геометриялық қосындысына тең.

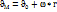
Жазық фигураның кез келген 2 нүктесінің жылдамдықтарының осы нүктелер арқылы жүргізілген түзу бағытындағы проекциялары тең.

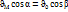
9.Ж:Л.Ц. Ж.л.ц.-берілген лездік уақыт t мезгілінде жылдамдығы 0-ге тең болатын жазық фигура жазықтығының бір нүктесін айтамыз. Егер жазық фигураның қандай да бір нүктесінің жылдамдығы берілсе және 2-шібір нүктенің жылдамдығының бағыты ғана белгілі болса, онда бұл фигура жазықтығының кез келген нүктелерінің жылдамдықтарын жылдамдықтардың лездік центрі арқылы табуға болады.

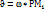
1тәсіл. Жылдамдықтардың таралу формулаларын пайдалану.

2тәсіл. Жылдамдықтар лездік центрін пайдалану.

10. Нүктенің күрделі қозғалысы.

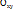-қозғалмайтын негізгі санақ жүйесі.

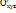(хуz- төбесінде штрих)- негізгі жүйеге қарағанда кез келген түрде қозғалыс жасай алатын өозғалмалы санақ жүйесі.

М материалық нүкте қозғалатын санақ жүйеге қарағанда өзі де қозғалыс жасайды және оның бұл қозғалысы 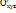(хуz- төбесінде штрих) жүйе қозғалысына тәуелсіз болады. Негізгі 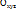жүйеге қатысты нүктенің қозғалысын шартты түрде абсолют немесе күрделі қозғалыс деп атайды.

М материалық нүктенің қозғалмалы 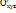(хуz- төбесінде штрих) жүйесіне қатысты қозғалысы салыстырмалы қозғалыс ретінде алынады.

Қозғалушы М материалық нүктенің жылжымалы жүйе 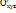(хуz- төбесінде штрих) жүйесіне ілесе қозғалуы оның тасымал қозғалыс ретінеде алынады.

11. Жылдамдықтарды қосу теоремасы.

Нүктенің абсолют жылдамдығы тасымал және салыстырмалы жылдамдықтардың векторлық қосындысына тең болады.

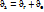
Нүктенің абсолют үдеуі тасымал,салыстырмалы және Кориолис үдеулерінің геометриялық қосындысына тең болады.

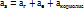
Дата добавления: 2015-06-04