Вычисление объемов тела вращения

Примеры для самостоятельной работы

Вычислить площади фигур, ограниченных линиями:

57. у = х ² + 1, х – у + 3 = 0; 58. у = х, у = 3 х, х = 2; 59. х ² + 1 – у = 0, у – 5 = 0;

60. х ² + у ² = 4, у = 2 х – х ² (х ³ 0, у ³ 0); 61. х ² + у ² = 4, х + у = 2;

62. , , х = 6; 63. 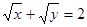, х + у = 4;

64. , ; 65. 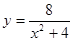, 2 у = х, х = 0.

Вычислить площади фигур, определяемых неравенствами:

66. 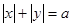; 67. ; 68. .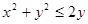

Перейдя к полярным координатам, найти площади фигур, ограниченных линиями:

69. х² + у² = 9, х² + у² – 6 х = 0, у = 0; 70. х² + у² – 4 х = 0, х² + у² – 4 у = 0;

71. (х² + у²) ² = 8(х² – у²), (х - 2) ² + у² = 4; 72. (х² + у²) ² = 18 ху.

Вычислить площади, ограниченные петлей кривой:

73. х³ + у³ = 8 ху; 74. (х + у) ⁴ = 3 х²у; 75. (х + у) ⁵ = 5х²у².

Вычислить площади фигур, ограниченных линиями:

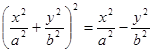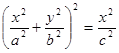76. ; 77. ; 78. .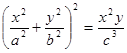

Произведя надлежащую замену переменных, найти площади фигур, ограниченных линиями:

79. ху = а, xy = b, y = kx, y = hx (0 < a < b, 0 < k < h);

80. (x + 2 y –1)² + (2 x + y - 2)² = 9.

Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f(x, y), снизу плоскостью z = 0 и с боков прямой цилиндрической поверхностью, вырезающей из плоскости Оху область D, находится по формуле

. (29)

Вычисление двойного интеграла в правой части формулы (29), в некоторых случаях упрощается при переходе к новым координатам.

Пример 32. Вычислить объем тела, ограниченного плоскостями х + 2 у – - z = 0, z = 0.

Данное тело ограничено сверху плоскостью х + 2 у – z = 0, или

z = х + 2 у,(30)

с боков – плоскостями

2 x + 3 y – 18 = 0, x – 2 y – 2 = 0, x = 3, (31)

параллельными оси Oz (уравнения не содержат координаты z) и снизу – плоскостью z = 0 (плоскость Оху).

В плоскости Оху (z = 0) уравнения (31) являются уравнениями прямых, по которым плоскости (31) пересекают плоскость Оху. Решая каждые два из них, находим три точки пересечения: А (3, 4), В (6, 2), . Следовательно, плоскости (31) вырезают в плоскости Оху область D, которая является треугольником АВС (рис. 43). На плоскости (30) точкам А, В, С будут соответствовать точки Р (3, 4, 11), Q (6, 2, 10), - вершины данного тела.

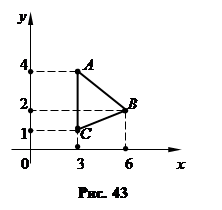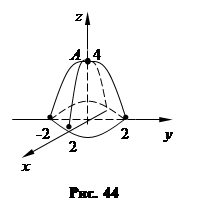Так как в этом случае z = f(x, y) = x + 2 y, пределы интегрирования по х: х₁ = 3, х₂ = 6; пределы интегрирования по у: 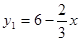, 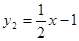(получено из уравнений прямых АВ и ВС), то по формуле (29) находим

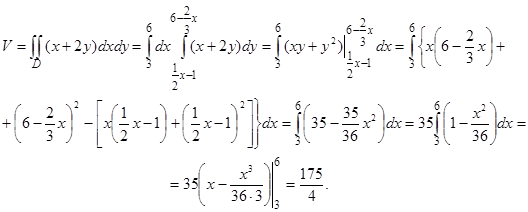
Пример 33. Вычислить объем тела, ограниченного поверхностью х² + у² + + z – 4 = 0 и плоскостью z = 0.

Разрешая первое уравнение относительно z, получаем z = 4 – x² – y². Это уравнение определяет параболоид вращения с вершиной в точке А (0, 0, 4), являющейся высшей точкой поверхности (рис. 44). Параболоид z = 4 – x² – y² и плоскость z = 0 пересекаются по окружности, уравнение которой в плоскости Оху имеет вид х² + у² = 4.

Формула (29) в данном случае запишется так: , где область D ограничена окружностью х² + у² = 4.

Чтобы вычислить интеграл, перейдем к полярным координатам, полагая x = r cos q, у = r sin q. Так как 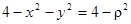, , r ₁ = 0, r ₂ = 2, q ₁ = 0, q ₂ = 2p, то

.

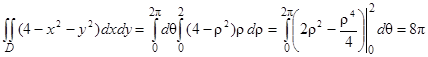Пример 34. Вычислить объем тела, ограниченного эллипсоидом

.

Разрешая это уравнение относительно z, находим .

Вычислим половину указанного объема, т.е. объем тела, ограниченного поверхностью 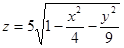и плоскостью z = 0 и представляющего часть эллипсоида, расположенную над плоскостью Оху (рис. 45).

0 х

		Рис. 46

По формуле (29) 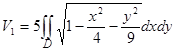, где область интегрирования D ограничена эллипсом 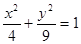, z = 0 (получено из уравнения поверхности).

Для вычисления интеграла переходим к обобщенным полярным координатам, полагая x = 2rcosq, у = 3r sinq. Так как 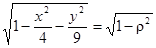, , 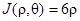q меняется от 0 до 2p, r - от 0 до 1, то

Следовательно, объем всего эллипсоида V = 2 V₁ = 40p.

Замечание. Объем V₁ можно вычислить по формуле

.

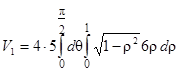Пример 35. Вычислить объем тела, ограниченного поверхностями х² + у² - - z = 0, x + y – z = 0.

Данное тело ограничено сверху плоскостью z = x + y, проходящей через биссектрису второго и четвертого координатных углов плоскости Оху, а снизу – параболоидом z = x² + y². Объем его равен разности объемов двух цилиндроидов с общим основанием на плоскости Оху. Это основание ограничено линией, представляющей собой проекцию на плоскость Оху линии пересечения данных поверхностей. Уравнение указанной проекции получается исключением z из данной системы уравнений: z = x² + y², z = x + y и имеет вид х² + у² = х + у, z = 0. Это уравнение окружности 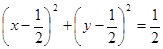, z = 0, ограничивающей область интегрирования D.

Следовательно,

Переходим к полярным координатам, полагая , .

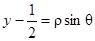Получаем

Пример 36. Вычислить объем тела, ограниченного поверхностями z = x² + + y², ху = р, ху = q, у = ах, у = bх, z = 0 (0 < p < q, 0 < a < b, х ³ 0, у ³ 0).

Указанное тело ограничено параболоидом z = x² + y², гиперболическими цилиндрами ху = р, ху = q, плоскостями у = ах, у = bх, координатной плоскостью Оху и расположено в первом октанте. Цилиндры и плоскости вырезают в первой четверти плоскости Оху криволинейный четырехугольник ABCD (см. рис. 46).

Объем тела , где D – четырехугольник ABCD.

Чтобы вычислить этот интеграл, введем криволинейные координаты по формулам: xy = u (p £ u £ q), y = vx (a £ v £ b). (Эти формулы подсказаны видом уравнений цилиндров и плоскостей.)

Так как , , ;

,

то

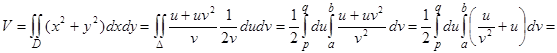
Дата добавления: 2015-06-04