Внутренние силы

В результате действия внешних сил в теле возникают внутренние силы.
Внутренняя сила — силы взаимодействия между частями одного тела, возникающие под действием внешних сил.

Внутренние силы являются самоуравновешенными, поэтому они не видны и не влияют на равновесие тела. Определяют внутренние силы методом сечения.

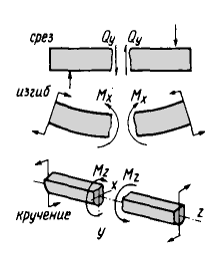
Внешние нагрузки приводят к следующим видам напряженно-деформированного состояния:

· Срез

· Изгиб

· Кручение

Для расчетов элементов конструкции на прочность необходимо знать внутренние силы упругости, возникающие в результате приложения внешних сил в разных точках и частях конструкции.
Способы определения этих внутренних сил с помощью науки сопротивление материалов включают такой прием, как метод сечений.

Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию).
При применении этого метода выгоднее отбрасывать ту часть элемента конструкции (тела), для которой проще составить уравнение равновесия. Таким образом, появляется возможность определить внутренние силовые факторы в сечении, благодаря которым оставшаяся часть тела находится в равновесии (прием, часто применяемый в Статике).

Применяя к оставленной части тела условия равновесия, невозможно найти закон распределения внутренних сил по сечению, но можно определить статические эквиваленты этих сил (равнодействующие силовые факторы).
Так как основным расчетным объектом в сопротивлении материалов является брус, рассмотрим, какие статические эквиваленты внутренних сил проявляются в поперечном сечении бруса.

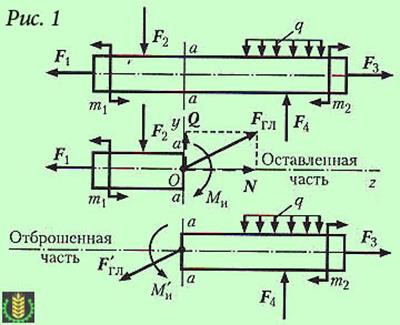
Рассечем брус (рис. 1) поперечным сечением а-а и рассмотрим равновесие его левой части.
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а-а, будут главный вектор Fгл, приложенный в центре тяжести сечения, и главный момент Мгл = Ми, уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.

Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющую Q, перпендикулярную этой оси и лежащую в плоскости сечения. Эти составляющие главного вектора и главный момент называютвнутренними силовыми факторами, действующими в сечении бруса. Составляющую N называют продольной силой, составляющую Q – поперечной силой, пару сил с моментом Ми – изгибающим моментом.

Для определения указанных трех внутренних силовых факторов применим известные из Статики уравнения равновесия оставленной части бруса:

Σ Z = 0; Σ Y = 0; Σ M = 0; (ось z всегда направляем по оси бруса).

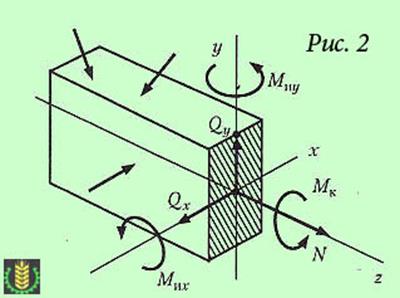
Если внешние силы, действующие на брус, не лежат в одной плоскости, т. е. представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов(рис. 2), для определения которых применяют известные из Статики шесть уравнений равновесия оставленной части бруса:

Σ X = 0; Σ Y = 0; Σ Z = 0;
Σ Mx = 0; Σ My = 0; Σ Mz = 0.

Эти силовые факторы в общем случае носят следующие названия:N – продольная сила, Qx, Qy – поперечные силы, Мкр – крутящий момент, Мих и Миу – изгибающие моменты.

При разных деформациях в поперечном сечении бруса возникают различные силовые факторы.
Рассмотрим частные случаи:

1. В сечении возникает только продольная сила N. Это деформация растяжения (если N направлена от сечения) или сжатия (если Nнаправлена к сечению).

2. В сечении возникает только поперечная сила Q. Это деформация сдвига.

3. В сечении возникает только крутящий момент Мкр. Это деформация кручения.

4. В сечении возникает только изгибающий момент Ми. Это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий моментМи и поперечная сила Q, то изгиб называют поперечным.

5. Если в сечении одновременно возникает несколько внутренних силовых факторов (например, изгибающий момент и продольная сила), то имеет место сочетание основных деформаций (сложное сопротивление).

11) Допущения о свойствах материалов и характере деформаций
Допущения о свойствах материалов:

1. Материал однороден, т. е. его свойства не зависят от размеров выделенного из тела объема. В действительности однородных материалов в природе нет. Например, структура металлов состоит из множества хаотически расположенных микроскопически мелких кристаллов (зерен). Размеры же рассчитываемых элементов конструкций, как правило, неизмеримо превышают размеры кристаллов, поэтому допущение об однородности материала здесь полностью применимо.
2. Материал представляет собой сплошную среду и непрерывно заполняет весь предоставленный ему объем. Это допущение вытекает непосредственно из первого - об однородности материала - и позволяет применять математический анализ.
3. Материал изотропен, т. е. физико-механические свойства одинаковы по всем направлениям. Таким образом, выделенный из сплошной среды элемент не зависит от ориентации относительно выбранной системы координат. Металлы благодаря своей мелкозернистой структуре считаются изотропными. Но есть много неизотропных - анизотропных - материалов. К ним относятся древесина, ткани, фанера, многие пластмассы. Однако в сопротив-лении материалов рассматриваются в основном материалы изотропные.
4. Материал в определенных пределах нагружения тела обладает идеальной упругостью, т. е. после снятия нагрузки тело полностью восстанавливает первоначальные формы и размеры.

Допущения о характере деформации элементов конструкций:

1. Перемещения точек элемента конструкции, обусловленные его упругими деформациями, незначительны по сравнению с размерами самого тела. Согласно этому допущению, деформированный элемент конструкции (или вся конструкция целиком) несущественно отличается от недеформированного. Поэтому при составлении уравнений равновесия сил, действующих на деформированное тело, можно пренебрегать теми изменениями, которые произошли в расположении сил, т. е. следует исходить из первоначальной формы тела (элемента конструкции) и его начальных размеров. Это положение кратко называется принципом начальных размеров.
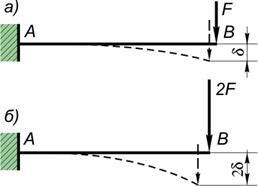
2. Перемещения точек упругого тела в известных пределах нагружения прямо пропорциональны силам, вызывающим эти перемещения. Например, если сила вызвала перемещение точки на расстояние 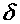(рис. а), то сила 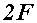вызовет перемещение точки 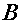на расстояние 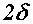(рис. б). Конструкции, для которых справедливо это допущение, называются линейно-деформируемыми.

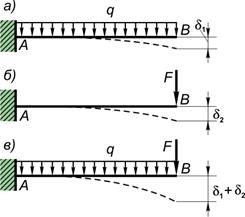
1. Для линейно-деформируемых конструкций справедлив известный из теоретической механики принцип независимости действия сил - результат действия нескольких сил не зависит от последовательности нагружения ими данной конструкции и равен сумме результатов действия каждой силы в отдельности. Следовательно, если под действием равномерно распределенной силы точка 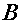бруса (рис. а) переместится на расстояние 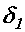; а под действием сосредоточенной силы (рис. б) - на расстояние 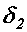, то при одновременном действии обеих сил перемещение точки 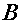равно сумме перемещени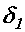й и 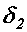(рис. в).

12)Классификация внешних сил. Реальный объект и расчетная схема
Внешними силами называют силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами. Если же нагрузка распределена по поверхности тела или его части, то такую нагрузку называют распределенной
В расчетной схеме нагрузку, распределенную по поверхности (рис. 1.2) приводят к плоскости, совпадающей с продольной осью, в результате чего получается нагрузка, распределенная по линии. Мерой такой нагрузки является ее интенсивность q - величина нагрузки на единицу длины. Размерность - Н/м. Равнодействующая распределенной нагрузки численно равна площади ее эпюры и приложена в центре ее тяжести.

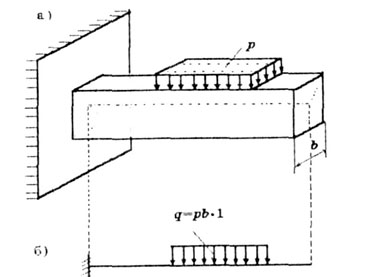
Рис. 1.2

Кроме тoro, встречаются нагрузки в виде сосредоточенного момента (пары сип). Есть несколько способов изображения моментов (рис. 1.3).

Рис. 1.3

Тогда М - это крутящий момент (рис. 1.4).

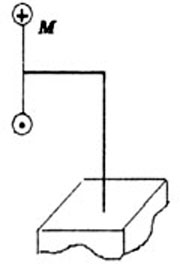
Рис. 1.4

Так изображается сипа, идущая к нам.

Так изображается сила, идущая от нас.
Реальный объект –исследуемый элемент конструкции,взятый с учетом всехсвоих особенностей: геометрических, физических, механических и других.

Рассчитать реальный объект практически невозможно (пришлось бы учитывать влияние слишком многих взаимосвязанных характеристик объекта), поэтому необходимо перейти к некоторой расчетной схеме (модели реального объекта) на основе определенной сис-темы гипотез, идеализирующих расчетную ситуацию.

Расчетная схема –это реальный объект,у которого отброшены все детали(особенности), не связанные с расчетом, а их влияние заменено силовыми воздействиями.

Основная цель сопротивления материалов – создать практически приемле-мые, простые приемы (методики) расчета типовых, наиболее часто встре-чающихся элементов конструкций. Необходимость перехода от реального объекта к расчетной схеме (с целью упрощения расчетов) заставляет вводить схематизацию понятий.

Можно выделить следующие типы схематизации:

геометрическая схематизация; физическая схематизация; силовая схематизация.

Геометрическая схематизация (модель формы)

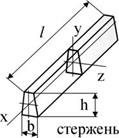Для схематизации формы реальных объектов в сопротивлении материалов используются следующие основные типы элементов: стержень (брус, балка,

вал), пластина (плита, оболочка) и массивное тело.

Стержень –элемент конструкции,у которого два измере-ния малы по сравнению с третьим.

Задачи по расчету стержней в основном являются одномерными (линейными, т. е. решение задачи зависит от одной переменной коор-динаты).

Пластина –элемент конструкции,у которого одно измерение(толщина)мало по сравнению с двумя другими.

Пластина криволинейная до нагружения называется оболочкой.

Задачи по расчету пластин в основном являются двумерными (плоскими)

Массивное тело –элемент конструкции,у которого все размеры имеют одинпорядок.

Задачи по расчету массивных тел в основном являются трехмерными (пространст-венными).

В сопротивлении материалов рассматриваются преимущественно одномерные задачи рас-чета стержневых элементов конструкций. Решение более сложных двумерных и трехмер-ных задач расчета пластин, оболочек и массивных тел рассматривает дисциплина, назы-ваемая «Теория упругости», которая основывается на меньшем количестве исходных ги-потез.

Физическая схематизация (модель материала)

Все изучаемые тела считаются выполненными (изготовленными) из материалов, условно наделенных определенными идеализированными свойствами.

Материал элементов конструкций будем в дальнейшем считать сплошным,

однородным, изотропным и линейно-упругим.

Сплошной материал –материал,не имеющий разрывов,пустот,трещин,пор,включений и т. д.

Считается, что материал непрерывно (сплошь) заполняет весь объем элемента конструк-ции, при этом не учитывается конкретная структура материала (зеренная, кристалличе-ская, волокнистая, слоистая и т. д.).

Однородный материал –материал,в каждой точке которого механическиесвойства одинаковы и не зависят от величины выделенного объема.

Изотропный материал –материал,свойства которого одинаковы по всем на-правлениям.

Таким образом, свойства изотропного материала не зависят от направления исследования, например, от направления приложения нагрузки при механических испытаниях.

В противном случае материал называется анизотропным (дерево, стеклопластик, слюда и др.).

Упругий материал –материал,обладающий способностью восстанавливатьпервоначальные форму и размеры тела после снятия внешней нагрузки.

Линейно-упругий материал –материал,подчиняющийся закону Гука.

Закон Гука: «Перемещения точек упругого тела(в известных пределах на-гружения) прямо пропорциональны силам, вызывающим эти перемещения».

Силовая схематизация (модель нагружения)

Для правильной постановки задачи в сопротивлении материалов весьма важно уметь классифицировать внешние силы (нагрузки), действующие на элементы конструкций.

Внешние силы –силы взаимодействия между рассматриваемым элементомконструкции и другими телами, связанными с ним.

Введем следующую классификацию внешних сил по способу приложения:

Сосредоточенные нагрузки –силы и моменты,площадьдействия которых мала по сравнению с размерами объекта (приложены в точке).

Обозначения: F (Р), М (T).

Единицы измерения: [ F ]=H; [ M ]=Н·м в СИ или [ F ]=кг; [ M ]=кг·м в технической системе.

Распределенные нагрузки –силы,действующие а)на не-

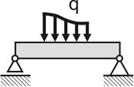
которой длине, б) по некоторой площадке, в) по объему.

Обозначение q.

Единицы измерения: а) [ q ]=H/м, кг/ см, кг/мм; б) [ q ]=H/м², кг/см², кг/мм²; в) [ q ]=H/м³, кг/см³, кг/мм³ и т. д.

Внешние нагрузки различают также по характеру изменения во времени: Статические нагрузки медленно и плавно возрастают от нуля до своего ко-нечного значения, а затем остаются неизменными.

Динамические нагрузки сопровождаются ускорениями как деформированно-го тела, так и взаимодействующих с ним тел.

К динамическим нагрузкам относятся, например, силы действующие на ускорено движу-щиеся тела, ударные нагрузки и т. д.

Повторно- переменные нагрузки –силы непрерывно и периодически изме-няющиеся во времени.

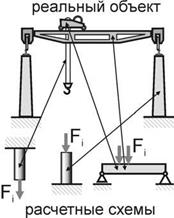
Теперь, введя рассмотренную схематизацию понятий, мы мо-жем переходить к работе с расчетными схемами, к их анализу. При этом отметим, что один и тот же реальный объект может иметь несколько расчетных схем, а одной и той же расчетной схеме может быть поставлено в соответствие много различных реальных объектов. В частности, при расчете мостового крана (см. рисунок) трос и опорная колонна будут рассчитываться по расчетной схеме растянутого или сжатого стержня, а каретка и направляющие – по схеме двухопорной балки и т. д. Отсюда вытекает еще одно определение сопротивления мате - риалов.

Сопротивление материалов –инженерная дисциплина,занимающаяся проч-ностным (в общем смысле) анализом наиболее типичных (часто встречаю-щихся) расчетных схем, годных для расчета любых элементов любых конструкций.

13) Внутренние усилия при растяжении и сжатии. Построение эпюр внутренних усилий. Понятие об опасном сечении.
Растяжение и сжатие

Растяжение (сжатие) - простой вид сопротивления, при котором стержень нагружен силами, параллельными продольной оси стержня и приложенными в центр тяжести его сечения.

Рассмотрим стержень, упруго растянутый центрально приложенными сосредоточенными силами P.

Прежде чем перейти к исследованию внутренних усилий и напряжений, возникающих в растянутом стержне, рассмотрим некоторые гипотезы, связанные с характером деформирования такого стержня и имеющие в сопротивлении материалов исключительно важное значение.

Принцип Сен-Венана: в сечениях, достаточно удаленных от мест приложения сил, распределение напряжений и деформаций мало зависит от способа приложения нагрузок.

Принцип Сен-Венана дает возможность вести расчет без учета местных (локальных) деформаций, возникающих вблизи точек приложения внешних сил и отличающихся от деформаций основного объема материала, что в большинстве случаев упрощает решение задачи.

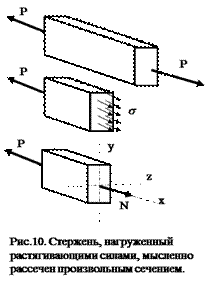Гипотеза плоских сече-ний (гипотеза Я.Бернулли): поперечные сечения стержня плоские и перпендикулярные его оси до деформации остаются плоскими и перпендикулярными оси, и после деформации.

Мысленно рассекая стер-жень, определим внутренние силы в растянутом стержне:

а) стержень, нагруженный растя-гивающими силами P и находя-щийся в равновесии, рассекаем произвольным сечением;

б) отбрасываем одну из частей стержня, а ее действие на дру-гую часть компенсируем вну-тренними усилиями интенсив-ностью ;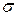

в) осевое внутреннее усилие N, возникающее в сечении стержня, определим, составляя уравнения равновесия для отсеченной части:

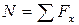. (2.1)

Проецируя внешнюю силу P, действующую на отсеченную часть стержня, на другие оси (z и y), а также составляя уравнения моментов относительно координатных осей, легко убедится, что осевое усилие N является единственным внутренним усилием, возникающим в сечении стержня (остальные тождественно равны нулю).

Таким образом, при растяжении (сжатии) из шести внутренних усилий в сечении стержня возникает только одно — продольная сила N.

Нормальные напряжения 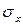, возникающие в сечении стержня, связаны с осевым усилием N следующим образом:

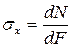, или 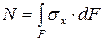. (2.2)

Учитывая, что в соответствии с гипотезой Бернулли напряжения равномерно распределены по поперечному сечению (т.е. 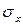=const), можно записать:

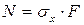. (2.3)

Таким образом, нормальные напряжения при растяжении (сжатии) определяются как

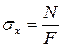. (2.4)

ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ ПРИ РАСТЯЖЕНИИ-СЖАТИИ

Растяжением или сжатием называется такой простой вид сопротивления, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только нормальная сила.

Рассмотрим расчетную схему бруса постоянного поперечного сечения с заданной внешней сосредоточенной нагрузкой Р и распределенной q, (рис.1).

а) расчетная схема, б) первый участок, левая отсеченная часть, в) второй участок, левая отсеченная часть, г) второй участок, правая отсеченная часть, д) эпюра нормальных сил

Рис.1. Построение эпюры нормальных сил:

Пусть 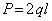. Прежде всего определим опорную реакцию R, задавшись ее направлением вдоль оси х.

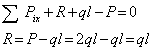
Брус имеет 2 участка 1 и 2.

В пределах первого участка мысленно рассечем брус на 2 части нормальным сечением и рассмотрим равновесие, допустим левой части, введя следующую координату х₁, рис.1 б:

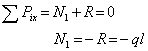
Следовательно, в пределах первого участка брус претерпевает сжатие постоянной нормальной силой.

Аналогично поступим со вторым участком. Мысленно рассечем его сечением 2—2, и рассмотрим равновесие левой части (рис.1 в).Установим предварительно границы изменения х₂:

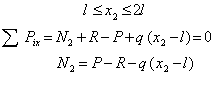
Подставляя граничные значения параметра х₂, получим:

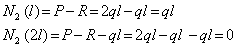
Таким образом, в пределах второго участка брус растянут и нормальная сила изменяется по линейному закону.

Аналогичный результат получается и при рассмотрении правой отсеченной части (рис.1 г):

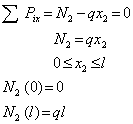
На основе полученных данных строится эпюра нормальных сил в виде графика распределения нормальной силы по длине бруса (рис.1 д). Характерно, что скачки на эпюре обусловлены наличием в соответствующих сечениях сосредоточенных сил R и Р, что в свою очередь может служить правилом правильности выполненных построений.

Для проверки на прочность при изгибе по действующим на балку внешним нагрузкам строят эпюры изменения внутренних усилий по ее длине и определяют опасные сечения балки, для каждого из которых необходимо провести проверку прочности.

При полной проверке прочности таких сечений будет, как минимум, три (иногда они совпадают):

1. сечение, в котором изгибающий момент Мх - достигает своего максималь­ного по модулю значения, - именно по этому сечению подбирают сечение всей балки;

2. сечение, в котором поперечная сила Qy, достигает своего максимального по модулю значения;

3. сечение, в котором и изгибающий момент Мx и поперечная сила Qy дости­гают по модулю достаточно больших величин.

В каждом из опасных сечений необходимо, построив эпюры нормальных и касательных напряжений, найти опасные точки сечения (проверка прочности проводится для каждой из них), которых также будет, как минимум, три:

1. точка, в которой нормальные напряжения 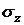, достигают своего макси­мального значения, - то есть точка на наружной поверхности балки наиболее удаленная от нейтральной оси сечения;

2. точка, в которой касательные напряжения 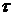достигают своего макси­мального значения, - точка, лежащая на нейтральной оси сечения;

точка, в которой и нормальные напряжения, и касательные напряжения, достигают достаточно больших величин (эта проверка имеет смысл
для сечений типа тавра или двутавра, где ширина резко изменяет свое значе­ние).

14) Условие прочности при кручении. Понятие об опасном сечении
Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде

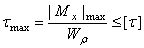, (5.6)

где 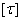берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:

- из второй теории прочности

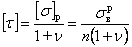; (5.7)

- из теории Мора

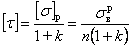, (5.8)

где .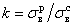

Из теорий прочности для пластичных материалов при чистом сдвиге получим:

- по третьей теории прочности

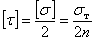, (5.9)

- по четвертой теории прочности

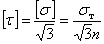. (5.10)

Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором , , 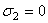, 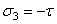то при повороте граней элемента на 45⁰ в новых площадках обнаруживаются только нормальные напряжения, равные по величине 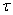(рис.5.8).

Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис.5.9,а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 45⁰, т.е. по направлению действия максимальных растягивающих напряжений (рис.5.9,б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис.5.9,в).

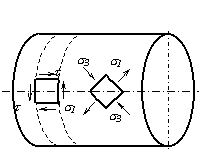
Рис.5.8 Рис.5.9

Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным 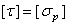- для хрупких материалов и 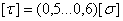- для пластичных материалов.

В опасном сечении вала при изгибе с кручением одновременно возникают наибольшие крутящий (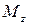) и результирующий изгибающий 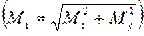момент.

15) Кручение. Напряжение при кручении. Эпюра касательных напряжений.
Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 5.1).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

Пусть вал вращается с постоянной скоростью n об/мин. и передает мощность N Нм/с. Угловая скорость вращения вала равна 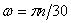(рад/сек), а передаваемая мощность .

Скручивающий момент равен .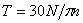

Если мощность задана в киловаттах, то величина скручивающего момента определяется по формуле

.

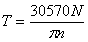НАПРЯЖЕНИЕ ПРИ КРУЧЕНИИ.

Если к концам вала приложены равные, но противоположно направленные внешние скручивающие моменты, то во всех его поперечных сечениях существуют только касательные напряжения, т.е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. В круговом поперечном сечении вала деформации сдвига и касательные напряжения равны нулю в центре и максимальны на краю; в промежуточных точках они пропорциональны расстоянию от центра тяжести сечения. Обычная формула для максимального касательного напряжения при кручении такова: S = Tc / J, где T – скручивающий момент на одном конце, c – радиус вала и J – полярный момент сечения. Для круга J = pr ⁴/2. Эта формула применима только в случае кругового поперечного сечения. Формулы для валов с поперечным сечением другой формы выводятся путем решения соответствующих задач методами математической теории упругости с привлечением в некоторых случаях методов экспериментального анализа.

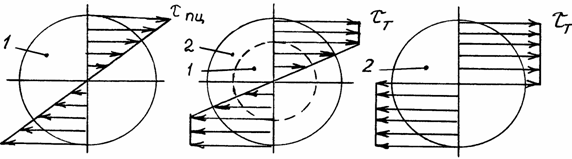а) б) в)

Рис. 2.9. Эпюры касательных напряжений при кручении

а) упругая стадия; б) стадия пластического деформирования;

в) стадия разрушения; 1 – упругая зона; 2 – пластическая зона

Дата добавления: 2015-06-04