Расчет составных систем

Под составными системами будем понимать конструкции, состоящие из нескольких тел, соединенных друг с другом.

Прежде, чем переходить к рассмотрению особенностей расчета таких систем, введем следующее определение.

Статически определимыми называются такие задачи и системы статики, для которых число неизвестных реакций связей не превышает максимально допустимого числа уравнений.

Если число неизвестных больше числа уравнений, соответствующие задачи и системы называются статически неопределимыми. При этом разность между числом неизвестных и числом уравнений называется степенью статической неопределимости системы.

Для любой плоской системы сил, действующих на твердое тело, имеется три независимых условия равновесия. Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных реакций связи.

В случае пространственной системы сил, действующих на твердое тело, имеется шесть независимых условия равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более шести неизвестных реакций связи.

Поясним это на следующих примерах.

1. Пусть центр невесомого идеального блока (пример 4) удерживается при помощи не двух, а трех стержней: АВ, ВС и BD и нужно определить реакции стержней, пренебрегая размерами блока.

С учетом условий задачи мы получим систему сходящихся сил, где для определения трех неизвестных: S_A, S_C и S_D можно составить по-прежнему систему только двух уравнений: Σ X = 0, Σ Y =0. Очевидно, поставленная задача и соответствующая ей система будут статически неопределимыми.

2. Балка, жестко защемленная на левом конце и имеющая на правом конце шарнирно-неподвижную опору, загружена произвольной плоской системой сил (рис.27).

Для определения опорных реакций можно составить только три уравнения равновесия, куда войдут 5 неизвестных опорных реакций: X_A, Y_A, M_A, X_B и Y_B. Поставленная задача будет дважды статически неопределимой.

Такую задачу нельзя решить в рамках теоретической механики, предполагая рассматриваемое тело абсолютно твердым.

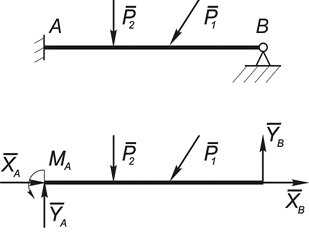
Рис.27

Вернемся к изучению составных систем, типичным представителем которых является трехшарнирная рама (рис. 28, а). Она состоит из двух тел: AC и BC, соединенным ключевым шарниром C. На примере этой рамы рассмотрим два способа определения опорных реакций составных систем.

1 способ. Рассмотрим тело AC, загруженное заданной силой Р, отбросив в соответствии с аксиомой 7 все связи и заменив их соответственно реакциями внешних (X_A, Y_A) и внутренних (X_C, Y_C) связей (рис. 28, б).

Аналогично можно рассмотреть равновесие тела BC под действием реакций опоры В - (X_B, Y_B) и реакций в соединительном шарнире C - (X_C’, Y_C ’), где в соответствии с аксиомой 5: X_C = X_C’, Y_C = Y_C ’.

Для каждого из этих тел можно составить три уравнения равновесия, таким образом, общее число неизвестных: X_A, Y_A, X_C = X_C’, Y_C = Y_C ’, X_B, Y_B равняется суммарному числу уравнений, и задача является статически определимой.

Напомним, что по условию задачи требовалось определить только 4 опорные реакции, нам же пришлось проделать дополнительную работу, определяя реакции в соединительном шарнире. В этом и заключается недостаток данного способа определения опорных реакций.

2 способ. Рассмотрим равновесие всей рамы АВС, отбросив только внешние связи и заменив их неизвестными опорными реакциями X_A, Y_A, X_B, Y_B.

Полученная система состоит из двух тел и не является абсолютно твердым телом, поскольку расстояние между точками А и В может изменяться вследствие взаимного поворота обеих частей относительно шарнира С. Тем не менее можно считать, что совокупность сил, приложенных к раме АВС образует систему, если воспользоваться аксиомой отвердевания (рис.28, в).

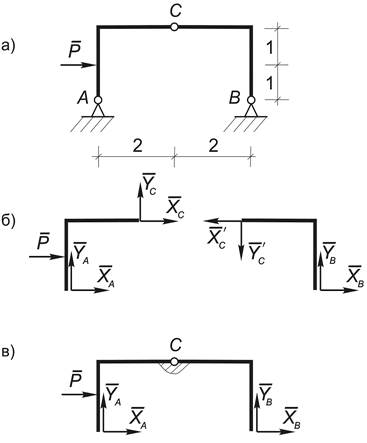
Рис.28

Итак, для тела АВС можно составить три уравнения равновесия. Например:

Σ M_A = 0;

Σ X = 0;

Σ Y = 0.

В эти три уравнения войдут 4 неизвестных опорных реакции X_A, Y_A, X_B и Y_B. Отметим, что попытка использовать в качестве недостающего уравнения, например такое: Σ M_В = 0 к успеху не приведет, поскольку это уравнение будет линейно зависимым с предыдущими. Для получения линейно независимого четвертого уравнения необходимо рассмотреть равновесие другого тела. В качестве него можно взять одну из частей рамы, например - ВС. При этом нужно составить такое уравнение, которое содержало бы «старые» неизвестные X_A, Y_A, X_B, Y_B и не содержало новых. Например, уравнение: Σ X ^(ВС) = 0 или подробнее: - X_С’ + X_B = 0 для этих целей не подходит, поскольку содержит «новое» неизвестное X_С ’, а вот уравнение Σ M_С ^(ВС) = 0 отвечает всем необходимым условиям. Таким образом, искомые опорные реакции можно найти в следующей последовательности:

Σ M_A = 0; → Y_B = Р /4;

Σ M_В = 0; → Y_А = - Р /4;

Σ M_С ^(ВС) = 0; → X_B = - Р /4;

Σ X = 0; → X_А = -3 Р /4.

Для проверки можно использовать уравнение: Σ M_С ^(АС) = 0 или, подробнее: - Y_А ∙2 + X_А ∙2 + Р ∙1 = Р /4∙2 -3 Р /4∙2 + Р ∙1 = Р /2 - 3 Р /2 + Р = 0.

Отметим, что в это уравнение входят все 4 найденные опорные реакции: X_А и Y_А - в явной форме, а X_B и Y_B - в неявной, поскольку они были использованы при определении двух первых реакций.

Графическое определение опорных реакций.

Во многих случаях решение задач можно упростить, если вместо уравнений равновесия или в дополнение к ним непосредственно использовать условия равновесия, аксиомы и теоремы статики. Соответствующий подход и получил название графического определения опорных реакций.

Прежде чем перейти к рассмотрению графического метода отметим, что, как и для системы сходящихся сил, графически можно решить только те задачи, которые допускают аналитическое решение. При этом графический метод определения опорных реакций удобен при небольшом числе нагрузок.

Итак, графический метод определения опорных реакций основан главным образом на использовании:

- аксиомы о равновесии системы двух сил;

- аксиомы о действии и противодействии;

- теоремы о трех силах;

- условия равновесия плоской системы сил.

При графическом определении реакций составных систем рекомендуется следующая последовательность рассмотрения:

- выбрать тело с минимальным числом алгебраических неизвестных реакций связей;

- если таких тел два или больше, то начать решение с рассмотрения тела, к которому приложено меньшее число сил;

- если таких тел два или больше, то выбрать тело, для которого большее число сил известно по направлению.

Решение задач.

При решения задач этого раздела сле­дует иметь в виду все те общие указания, которые были сделаны ранее.

Приступая к решению, надо, прежде всего, установить, равновесие какого именно тела следует в данной задаче рассмотреть. Затем, выделив это тело и рассматривая его как свободное, следует изобразить все действующие на тело заданные силы и реакции отброшенных связей.

Далее следует составить условия равновесия, применяя ту из форм этих условий, которая приводит к более простой системе урав­нений (наиболее простой будет система уравнений, в каждое из ко­торых входит по одному неизвестному).

Для получения более простых уравнений следует (если это только не усложняет ход расчета):

1) составляя уравнения проекций, проводить координатную ось, перпендикулярно какой-нибудь неиз­вестной силе;

2) при составлении моментного уравнения в качестве моментной целесообразно выбирать точку, где пересекаются линии действия двух неизвестных опорных реакций из трех – в этом случае они не войдут в уравнение, и оно будет содержать только одно неизвестное;

3) если две неизвестных опорных реакции из трех параллельны, то при составлении уравнения в проекциях на ось последнюю следует направить так, чтобы она была перпендикулярна к двум первым реакциям – в этом случае уравнение будет содержать только последнее неизвестное;

4) при решении задачи систему координат надо выбирать так, чтобы ее оси были ориентированы так же, как большинство приложенных к телу сил системы.

При вычислении моментов иногда бывает удобно разла­гать данную силу на две составляющие и, пользуясь теоремой Вариньона, находить момент силы как сумму моментов этих соста­вляющих.

Решение многих задач статики сводится к определению реакций опор, с помощью которых закрепляются балки, мостовые фермы и т. п.

Пример 7. К кронштейну, изображенному на рис.29, а, в узле В подвешен груз весом 36 кН. Соединения элементов кронштейна шарнирные. Определить усилия, возникающие в стержнях АВ и ВС, считая их невесомыми.

Решение. Рассмотрим равновесие узла В, в котором сходятся стержни АВ и ВС. Узел В представляет собой точку на чертеже. Так как груз подвешен к узлу В, то в точке В прикладываем силу F, равную весу подвешенного груза. Стержни ВА и ВС, шарнирно соединенные в узле В, ограничивают возможность любого его линейного перемещения в вертикальной плоскости, т.е. являются связями по отношению к узлу В.

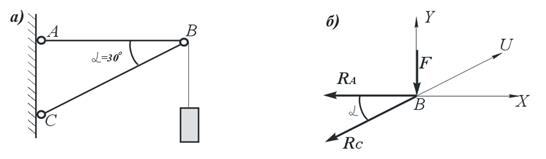
Рис. 29. Расчетная схема кронштейна к примеру 7:

а – расчетная схема; б – система сил в узле B

Мысленно отбрасываем связи и заменяем их действия силами - реакциями связей R_А и R_С. Так как стержни невесомые, то реакции этих стержней (усилия в стержнях) направлены вдоль оси стержней. Предположим, что оба стержня растянуты, т.е. их реакции направлены от шарнира внутрь стержней. Тогда, если после расчета реакция получится со знаком минус, то это будет означать, что на самом деле реакция направлена в сторону, противоположную указанной на чертеже, т.е. стержень будет сжат.

На рис. 29, б показано, что в точке В приложены активная сила F и реакции связей R_А и R_С. Видно, что изображенная система сил представляет плоскую систему сил, сходящихся в одной точке. Выбираем произвольно оси координат OX и OY и составляем уравнения равновесия вида:

Σ F_x = 0; -R_a - R_ccos 𝛼 = 0;

Σ F_y = 0; -F - R_c cos (90 - α) = 0.

Учитывая, что cos (90 - α ) = sin α, из второго уравнения находим

R_c = -F/sin α = -36/0,5 = -72 кН.

Подставив значение R_c в первое уравнение, получим

R_a = -R_c cos α= - (-72) ∙0,866 = 62,35 кН.

Таким образом, стержень АВ - растянут, а стержень ВС - сжат.

Для проверки правильности найденных усилий в стержнях спроектируем все силы на любую ось, не совпадающую с осями X и Y, например, ось U:

Σ F_u = 0; - R_c - R_a cos α - F cos (90- α) = 0.

После подстановки значений найденных усилий в стержнях (размерность в килоньютонах) получим

- (-72) – 62,35∙0,866 - 36∙0,5 = 0; 0 = 0.

Условие равновесия выполняется, таким образом, найденные усилия в стержнях верны.

Пример 8. Балка строительных подмостей, весом которой можно пренебречь удерживается в горизонтальном положении гибкой тягой СD и шарнирно опирается на стену в точке А. Найти усилие в тяге СD, если на край подмостей встанет рабочий весом 80 кг ≈0,8 кН (рис.30, а).

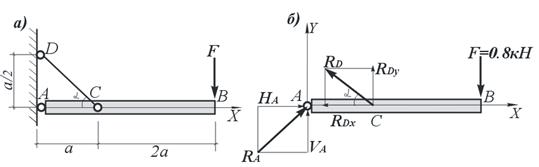
Рис. 30. Расчетная схема подмостей к примеру 8:

а – расчетная схема; б – система сил действующих на подмости

Решение. Выделяем объект равновесия. В данном примере объектом равновесия является балка подмостей. В точке В на балку действует активная сила F, равная весу человека. Связями в данном случае являются неподвижный опорный шарнир А и тяга CD. Мысленно отбросим связи, заменив их действие на балку, реакциями связей (рис. 30, б). Реакцию неподвижной шарнирной опоры по условию задачи определять не нужно. Реакция в тяге CD направлена вдоль тяги. Предположим, что стержень CD растянут, т.е. реакция R_D направлена от шарнира С внутрь стержня. Разложим реакцию R_D, по правилу параллелограмма, на горизонтальную и вертикальную составляющие:

R_Dx^гор =R_D cos α;

R_Dy^верт = R_D cos (90-α) = R_D sin α.

В результате получили произвольную плоскую систему сил, необходимым условием равновесия которой является равенство нулю трех независимых условий равновесия,.

В нашем случае удобно первым записать условие равновесия в виде суммы моментов относительно моментной точки А, так как момент опорной реакции R_A относительно этой точки равен нулю:

Σ m_A = 0; F ∙3 a - R _dy∙ a = 0

или

F ∙3 a - R_D sin α = 0.

Значение тригонометрических функций определим из треугольника АСD:

cosα = АC/CD = 0,89,

sinα = AD/CD = 0,446.

Решая уравнение равновесия, получим R _D = 5,38 кH. (Тяж СD - растянут).

Для проверки правильности вычисления усилия в тяже CD необходимо вычислить хотя бы одну из составляющих опорной реакции R_A. Воспользуемся уравнением равновесия в виде

Σ F_y = 0; V_A + R_Dy - F = 0

или

V_A = F - R_dy.

Отсюда V_A = -1,6 кН.

Знак минус означает, что вертикальная составляющая реакции R_A на опоре направлена вниз.

Проверим правильность вычисления усилия в тяже. Используем еще одно условие равновесия в виде уравнений моментов относительно точки В.

Σ m_B = 0; V_A ∙3 а + R_Dy∙ 2 a = 0;

-1,6∙3 а + 5,38∙0,446∙2 а = 0; 0 = 0.

Условия равновесия соблюдаются, таким образом, усилие в тяже найдено верно.

Пример 9. Вертикальный бетонный столб забетонирован нижним концом в горизонтальное основание. Сверху на столб передается нагрузка от стены здания весом 143 кН. Столб изготовлен из бетона плотностью γ= 25 кН/м³. Размеры столба показаны на рис. 31, а. Определить реакции в жесткой заделке.

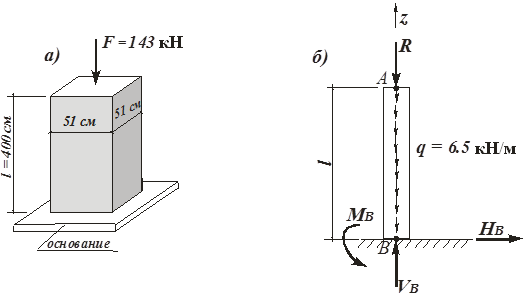
Рис. 31. Расчетная схема столба к примеру 9:

а – схема загрузки и размеры столба; б – расчетная схема

Решение. В данном примере объектом равновесия является столб. Столб загружен следующими типами активных нагрузок: в точке А сосредоточенной силой F, равной весу стены здания, и собственным весом столба в виде равномерно распределенной по длине бруса нагрузки интенсивностью q на каждый метр длины столба: q = 𝛾А, где А - площадь поперечного сечения столба.

q = 25∙0,51∙0.51 = 6,5 кН/м.

Связями в данном примере является жесткая заделка в основании столба. Мысленно отбросим заделку и заменим ее действие реакциями связей (рис. 31, б).

В нашем примере рассматривается частный случай действия системы сил, перпендикулярных заделке и проходящих по одной оси через точку приложения опорных реакций. Тогда две опорные реакции: горизонтальная составляющая и реактивный момент будут равны нулю. Для определения вертикальной составляющей опорной реакции спроектируем все силы на ось элемента. Совместим эту ось с осью Z, тогда условие равновесия запишется в следующем виде:

Σ F_Z = 0; V_B - F - ql = 0,

где ql - равнодействующая распределенной нагрузки.

Отсюда

V_B = F +ql= 143 + 6,5∙4 = 169 кН.

Знак плюс указывает, что реакция V_B направлена вверх.

Для проверки правильности вычисления опорной реакции остается еще одно условие равновесия - в виде алгебраической суммы моментов всех сил относительно любой точки, не проходящей через ось элемента. Предлагаем выполнить эту проверку самостоятельно.

Пример 10. Для балки, изображенной на рис.32, а, требуется определить опорные реакции. Дано: F = 60 кН, q = 24 кН/м, М = 28 кН∙м.

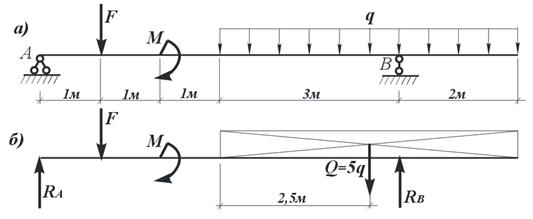
Рис. 32. Расчетная схема и размеры балки к примеру 10:

а – расчетная схема; б – объект равновесия

Решение. Рассмотрим равновесие балки. Балка загружена активной нагрузкой в виде плоской системы параллельных вертикальных сил, состоящих из сосредоточенной силы F, равномерно распределенной нагрузки интенсивностью q с равнодействующей Q, приложенной в центре тяжести грузовой площади (рис. 32, б), и сосредоточенного момента М, который можно представить в виде пары сил.

Связями в данной балке являются шарнирно-неподвижная опора А и шарнирно-подвижная опора В. Выделим объект равновесия, для этого отбросим опорные связи и заменим их действия реакциями в этих связях (рис. 32, б). Реакция подвижной опоры R_B направлена вертикально, а реакция шарнирно-неподвижной опоры R_A будет параллельна активной системе действующих сил и направлена также вертикально. Предположим, что они направлены вверх. Равнодействующая распределенной нагрузки Q = 4,8∙q приложена в центре симметрии грузовой площади.

При определении опорных реакций в балках необходимо стремиться так составлять уравнения равновесия, чтобы в каждое из них входило только одно неизвестное. Этого можно добиться, составляя два уравнения моментов относительно опорных точек. Проверку опорных реакций обычно проводят, составляя уравнение в виде суммы проекций всех сил на ось, перпендикулярную оси элемента.

Примем условно направление вращения момента опорных реакций вокруг моментных точек за положительное, тогда противоположное направление вращения сил будем считать отрицательным.

Необходимым и достаточным условием равновесия в данном случае является равенство нулю независимых условий равновесия в виде:

Σ m_A = 0; V_B ∙6 - q ∙4,8∙4,8 + M + F ∙2,4 = 0;

Σ m_B = 0; V_A ∙6 - q ∙4,8∙1,2 - M - F ∙8,4 = 0.

Подставляя численные значения величин, находим

V_B = 14,4 кН, V_A = 15,6 кН.

Для проверки правильности найденных реакций используем условие равновесия в виде:

Σ F_y = 0; V_A + V_B - F -q ∙4,8 =0.

После подстановки численных значений в это уравнение получаем тождество типа 0=0. Отсюда делаем выводы, что расчет выполнен верно и реакции на обеих опорах направлены вверх.

Пример 11. Определить опорные реакции для балки, изображенной на рис.33, а. Дано: F = 2,4 кН, M = 12 кН∙м, q = 0,6 кН/м, a = 60°.

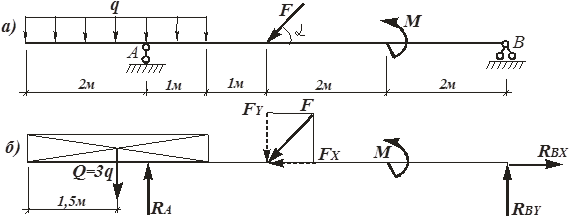
Рис. 33. Расчетная схема и размеры балки к примеру 11:

а – расчетная схема; б – объект равновесия

Решение. Рассмотрим равновесие балки. Мысленно освобождаем балку от связей на опорах и выделяем объект равновесия (рис. 33, б). Балка загружена активной нагрузкой в виде произвольной плоской системы сил. Равнодействующая распределенной нагрузки Q = q ∙3 приложена в центре симметрии грузовой площади. Силу F разложим по правилу параллелограмма на составляющие – горизонтальную и вертикальную

F_z = F cosα= 2,4 cos 60° = 1,2 кН;

F_y =F cos(90-α) = F sin 60° = 2,08 кН.

Прикладываем к объекту равновесия вместо отброшенных связей реакции. Предположим, вертикальная реакция V_A шарнирно подвижной опоры А направлена вверх, вертикальная реакция V_B шарнирно неподвижной опоры B направлена также вверх, а горизонтальная реакция H_В - вправо.

Таким образом, на рис. 33, б изображена произвольная плоская система сил, необходимым условием равновесия которой является равенство нулю трех независимых условий равновесия для плоской системы сил. Напомним, что, согласно теореме Вариньона, момент силы F относительно любой точки равен сумме моментов составляющих F_z и F_y относительно этой же точки. Примем условно, направление вращения момента опорных реакций вокруг моментных точек за положительное, тогда противоположное направление вращение сил будем считать отрицательным.

Тогда условия равновесия удобно составить в следующем виде:

Σ Fz = 0; - F_z + H_B = 0; отсюда H_B = 1,2 кН;

Σ m_A = 0; V_B ∙6 + M - F_y ∙2 + 3 q ∙0.5 = 0; отсюда V_B = - 1,456 кН;

Σ m_B = 0; V_A ∙6 - 3 q ∙6,5 - F_y ∙4 - M = 0; отсюда V_A = 5,336 кН.

Для проверки правильности вычисленных реакций используем еще одно условие равновесия, которое не использовали, например:

Σ F_y = 0; V_A + V_B - 3 q - F_y = 0.

После подстановки численных значений получаем тождество 0=0.

Вертикальная опорной реакции V_B получилась со знаком минус, это показывает, что в данной балке она направлена не вверх, а вниз.

Пример 12. Определить опорные реакции для балки, жестко заделанной с одной стороны и изображенной на рис. 34, а. Дано: q =20 кН/м.

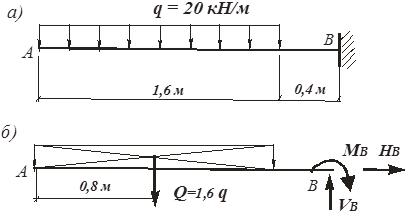
Рис. 34. Расчетная схема и размеры балки к примеру 12:

а – расчетная схема; б – объект равновесия

Решение. Выделим объект равновесия. Балка загружена активной нагрузкой в виде плоской системы параллельных сил, расположенных вертикально. Мысленно освобождаем балку от связей в заделке и заменяем их реакциями в виде сосредоточенной силы V_B и пары сил с искомым реактивным моментом М_B (см. рис.34, б). Так как активные силы действуют только в вертикальном направлении, то горизонтальная реакция Н_B равна нулю. Примем условно направление вращения момента опорных реакций вокруг моментных точек по часовой стрелке за положительное, тогда противоположное направление вращения сил будем считать отрицательным.

Составляем условия равновесия в виде

Σ F_y = 0; V_B - q ∙1,6 = 0;

Σ m_B = 0; M_B - q ∙1,6∙1,2 = 0.

Здесь q ∙1,6 – равнодействующая распределенной нагрузки.

Подставив численные значения распределенной нагрузки q, находим

V_В = 32 кН, М_B = 38,4 кН∙м.

Для проверки правильности найденных реакций составим еще одно условие равновесия. Теперь возьмем за моментную точку какую-нибудь другую точку, например правый конец балки, тогда:

Σ m_A = 0; M_B – V_B ∙2 + q ∙1,6∙0,8 = 0.

После подстановки численных значений получаем тождество 0=0.

Окончательно делаем выводы, что опорные реакции найдены верно. Вертикальная реакция V_B направлена вверх, а реактивный момент М_В - по часовой стрелке.

Пример 13. Определить опорные реакции балки (рис.35, а).

Решение. В качестве активной нагрузки выступает равнодействующая распределенной нагрузки Q =(1/2)∙ aq =(1/2)∙3∙2=3кН, линия действия которой проходит на расстоянии 1 м от левой опоры, сила натяжения нити Т = Р = 2 кН, приложенная на правом конце балки и сосредоточенный момент.

Поскольку последний можно заменить парой вертикальных сил, то действующая на балку нагрузка вместе с реакцией подвижной опоры В образует систему параллельных сил, поэтому реакция R_A будет также направлена вертикально (рис.35, б).

Для определения этих реакций воспользуемся уравнениями равновесия.

Σ M_A = 0; - Q ∙1 + R_В ∙3 - M + Т ∙5 = 0,

откуда

R_В = (1/3) (Q + M - Р ∙5) = (1/3) (3 + 4 - 2∙5) = -1 кН.

Σ M_B = 0; - R_A ∙3 + Q ∙2 - M + Т ∙2 = 0,

R_A = (1/3) (Q ∙2 - M + Р ∙2) = (1/3) (3∙2 - 4 + 2∙2) = 2 кН.

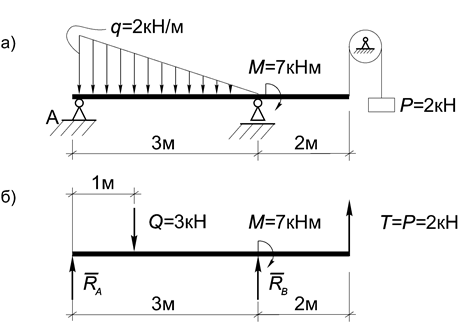
Рис.35

Чтобы проверить правильность полученного решения, воспользуемся дополнительным уравнением равновесия:

Σ Y_i = R_A - Q + R_В + Т = 2 - 3 - 1 + 2 = 0,

то есть, задача решена правильно.

Пример 14. Найти опорные реакции консольной балки, загруженной распределенной нагрузкой (рис.36, а).

Решение. Равнодействующая распределенной нагрузки приложена в центре тяжести грузовой эпюры. Чтобы не искать положение центра тяжести трапеции, представим ее в виде суммы двух треугольников. Тогда заданная нагрузка будет эквивалентна двум силам: Q ₁ = (1/2)∙3∙2 = 3 кН и Q ₂ = (1/2)∙3∙4 = 6 кН, которые приложены в центре тяжести каждого из треугольников (рис.36, б).

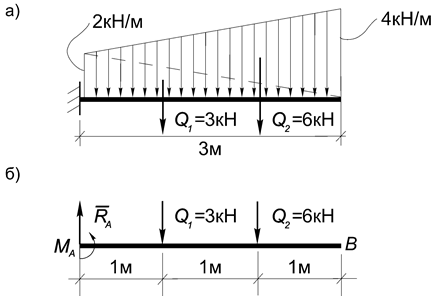
Рис.36

Опорные реакции жесткого защемления представлены силой R_A и моментом M_A, для определения которых удобнее использовать уравнения равновесия системы параллельных сил, то есть:

Σ M_A = 0; M_A = 15 кН∙м;

Σ Y = 0, R_A = 9 кН.

Для проверки воспользуемся дополнительным уравнением Σ M_В = 0, где точка В находится на правом конце балки:

Σ M_В = M_A - R_A ∙3 + Q ₁∙2 + Q ₂∙1 = 15 - 27 + 6 +6 = 0.

Пример 15. Однородная балка весом Q = 600 Н и длиной l = 4 м опирается одним концом на гладкий пол, а промежуточной точкой В на столб высотой h = 3 м, образуя с вертикалью угол 30°. В таком положении балка удерживается веревкой, протянутой по полу. Определить натяжение веревки T и реакции столба - R_B и пола - R_A (рис.37, а).

Решение. Под балкой или стержнем в теоретической механике понимают тело, у которого поперечными размерами в сравнении с его длиной можно пренебречь. Таким образом, вес Q однородной балки приложен в точке С, где АС = 2 м.

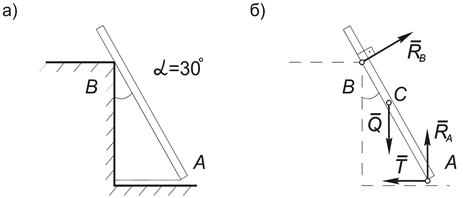
Рис.37

1) Поскольку две неизвестных реакции из трех приложены в точке А, первым следует составить уравнение Σ M_A = 0, так как туда войдет только реакция R_B:

- R_B ∙ АВ + Q ∙(l /2)∙sin30° = 0,

где АВ = h /cos30°= 2 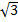м.

Подставляя в уравнение, получим:

R_B ∙2 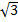= 600∙2∙(1/2) = 600,

откуда

R_B = 600/ (2 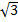) = 100 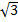≅ 173 Н.

Аналогично из моментного уравнения можно было бы найти и реакцию R_A, выбрав в качестве моментной точку, где пересекаются линии действия R_B и Т. Однако это потребует дополнительных построений, поэтому проще воспользоваться другими уравнениями равновесия:

2) Σ X = 0; R_B ∙cos30° - Т = 0; → Т = R_B ∙cos30°= 100 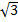∙( 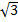/2) = 150 Н;

3) Σ Y = 0, R_B ∙sin30°- Q + R_A = 0; → R_A = Q - R_B ∙sin30°= 600 - 50 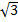≅ 513 Н.

Таким образом, мы нашли Т и R_A через R_B, поэтому проверить правильность полученного решения можно с помощью уравнения: Σ M_B = 0, куда в явном или неявном виде войдут все найденные реакции:

R_A ∙ АВ sin30°- Т ∙ АВ cos30° - Q ∙(АВ - l /2)∙sin30°= 513∙2 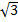∙(1/2) - 150∙2 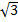∙( 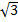/2) - 600∙ (2 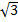- 2)∙(1/2) = 513∙ 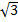- 150∙3 - 600∙( 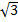-1) ≅ 513∙1,73 - 450 - 600∙0,73 = 887,5 - 888 = -0,5.

Полученная в результате округления невязка ∆= -0,5 называется абсолютной погрешностью вычисления.

Для того чтобы ответить на вопрос насколько точным является полученный результат, вычисляют относительную погрешность, которая определяется по формуле:

ε=[|∆| / min(|Σ⁺|, |Σ^-|)]∙100% =[|-0,5| / min(|887,5|, |-888|)]∙100% = (0,5/887,5)∙100% = 0,06%.

Пример 16. Определить опорные реакции рамы (рис.38). Здесь и в дальнейшем, если не оговорено специально, все размеры на рисунках будем считать указанными в метрах, а силы - в килоньютонах.

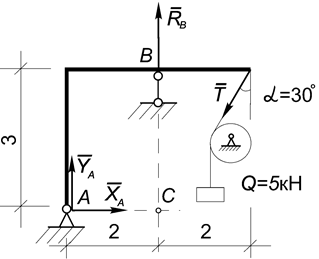
Рис.38

Решение. Рассмотрим равновесие рамы, к которой в качестве активной приложена сила натяжения нити Т, равная весу груза Q.

1) Реакцию подвижной опоры R_B найдем из уравнения Σ M_A = 0. Чтобы при этом не вычислять плечо силы Т, воспользуемся теоремой Вариньона, разложив эту силу на горизонтальную и вертикальную составляющие:

R_B ∙2 + Т sin30°∙3 - Т cos30°∙4 = 0; → R_B = (1/2)∙ Q (cos30°∙4 - sin30°∙3) = (5/4) ∙ (4 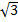- 3) кН.

2) Для вычисления Y_A составим уравнение Σ M_С = 0, где точка С лежит на пересечении линий действия реакций R_B и Х_A:

- Y_A ∙2 + Т sin30°∙3 - Т cos30°∙2 = 0; → Y_A = (1/2)∙ Q (sin30°∙3 -cos30°∙2) = (5/4) ∙ (3 -2 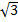) кН.

3) Наконец, находим реакцию Х_A:

Σ X = 0; Х_A - Т sin30° = 0; → Х_A = Q sin30° = 5/2 кН.

Поскольку все три реакции были найдены независимо друг от друга, для проверки нужно взять уравнение, в которое входит каждая из них:

Σ M_D = Х_A ∙3 - Y_A ∙4 - R_B ∙2 = 15/2 - 5∙(3 -2 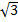) - (5/2)∙ (4 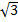- 3) = 15/2 - 15 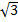+ 10 -10 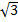+15/2 = 0.

Пример 17. Определить опорные реакции стержня, имеющего ломаное очертание (рис.39, а).

Решение. Заменяем распределенную нагрузку на каждом участке стержня сосредоточенными силами Q ₁ = 5 кН и Q ₂ = 3 кН, а действие отброшенного жесткого защемления - реакциями Х_A, Y_A и M_А (рис.39, б).

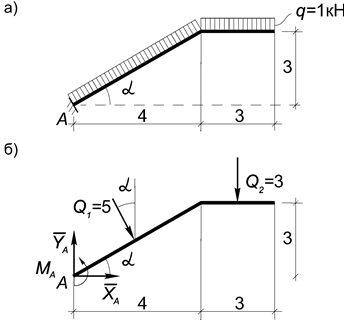
Рис.39

1) Σ M_А = 0; M_А - Q ₁∙2,5 - Q ₂∙5,5 = 0; → M_А = 5∙2,5 + 3∙5,5 = 12,5 + 16,5 = 29 кНм.

2) Σ X = 0; Х_A + Q ₁∙sina = 0; → Х_A = -5∙(3/5) = -3 кН.

3) Σ Y = 0; Y_A - Q ₁ cosa - Q ₂ = 0; → Y_A = 5∙(4/5) + 3 = 4 + 3 = 7 кН, так как sinα = 3/5, cosα = 4/5.

Проверка: Σ M_В = 0; M_А + Х_A ∙3 - Y_A ∙7 + Q ₁cosα∙4,5 + Q ₁sinα∙1,5 + Q ₂∙1,5 = 29 -3∙3 - 7∙7 + 5∙(4/5)∙5 + 5∙(3/5)∙1,5 + 3∙1,5 = 29 - 9 - 49 + 20 + 4,5 + 4,5 = 58 - 58 = 0.

Пример 18. Для рамы изображенной на рис.40, а, требуется определить опорные реакции. Дано: F = 50 кН, М = 60 кН∙м, q = 20 кН/м.

Решение. Рассмотрим равновесие рамы. Мысленно освобождаем раму от связей на опорах (рис.40, б) и выделяем объект равновесия. Рама загружена активной нагрузкой в виде произвольной плоской системы сил. Вместо отброшенных связей прикладываем к объекту равновесия реакции: на шарнирно-неподвижной опоре А - вертикальную V_A и горизонтальную H_A, а на шарнирно-подвижной опоре В - вертикальную реакцию V_B Предполагаемое направление реакций показано на рис.40, б.

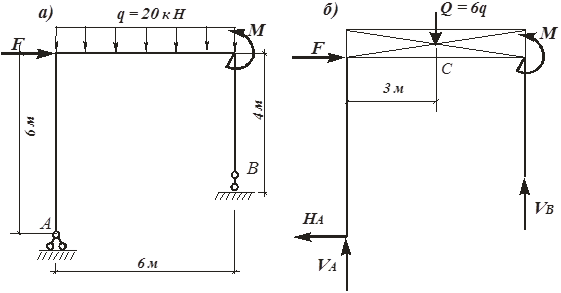
Рис.40. Расчетная схема рамы и объект равновесия к примеру 18:

а – расчетная схема; б – объект равновесия

Составляем следующие условия равновесия:

Σ F_x = 0; - H_A + F = 0; H_A = 50 кН.

Σ m_A = 0; V_B ∙6 + M - q ∙6∙3 - F ∙6 = 0; V_B = 100 кН.

Σ F_y = 0; V_A + V_B - q ∙6 = 0; V_A = 20 кН.

Здесь условно принято направление вращения вокруг моментных точек против движения часовой стрелки за положительное.

Для проверки правильности вычисления реакций используем условие равновесия, в которое входили бы все опорные реакции, например:

Σ m_C = 0; V_B ∙3 + M – H_A ∙6 – V_A ∙3 = 0.

После подстановки численных значений получаем тождество 0=0.

Таким образом, направления и величины опорных реакций определены верно.

Пример 19. Определить опорные реакции рамы (рис.41, а).

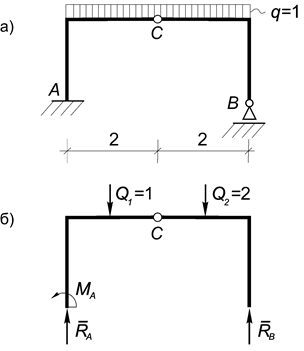
Рис.41

Решение. Как и в предыдущем примере, рама состоит из двух частей, соединенных ключевым шарниром С. Распределенную нагрузку, приложенную к левой части рамы, заменяем равнодействующей Q ₁, а к правой - равнодействующей Q ₂, где Q ₁ = Q ₂ = 2кН.

1) Находим реакцию R_B из уравнения Σ M_С ^(ВС) = 0; → R_B = 1кН;

Рассмотрим равновесие всей рамы как абсолютно твердого тела. Поскольку Q ₁, Q ₂и R_B образуют систему параллельных сил, реакции в точке А будут представлены вертикально направленной силой R_А и реактивным моментом М_А (рис.37, б), поэтому можно составить следующие уравнения равновесия:

2) Σ M_А = 0; → M_А = 4 кН∙м;

3) Σ Y = 0; → R_А = 3 кН.

Проверка:

Σ M_С ^(АС) = M_А - R_А ∙2 + Q ₁∙1 = 4 - 3∙2 + 2∙1 = 6 - 6 = 0.

Пример 20. Определить опорные реакции рамы (рис.42, а).

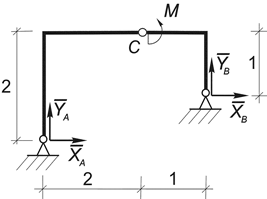
Рис.42

Решение. В отличие от двух предыдущих примеров формальное определение опорных реакции в этой задаче требует совместного рассмотрения системы уравнений:

Σ M_А =0; M + Y_В ∙3 - X_B ∙1 = 0;

Σ M_С ^(СВ) =0; M + Y_В ∙1 + X_B ∙1 = 0.

Ее решением будет: X_B = - M /2; Y_В = - M /2.

Рассматривая затем равновесие всей рамы в целом, получим:

Σ Х = 0; X_А + X_B = 0; → X_А = M /2;

Σ Y = 0; Y_А + Y_В = 0; → Y_А = M /2.

Проверка. Σ M_С ^(АС) = X_А ∙1 - Y_А ∙3 + M = M /2 - M /2 + M = 0.

Пример 21. Определить реакции в опорах и в соединительном шарнире трехшарнирной арки (рис.43, а).

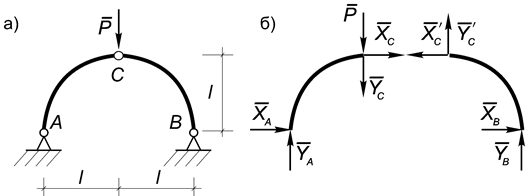
Рис.43

Решение. Находим опорные реакции:

1) Σ M_А = 0; → Y_В = Р /2;

2) Σ M_С ^(СВ) = 0; → Х_В = -Р /2;

3) Σ M_В = 0; → Y_А = Р /2;

4) Σ Х = 0; → X_А = Р /2.

Для определения реакций в соединительном шарнире нужно рассмотреть равновесие одной из частей рамы. При этом результат будет зависеть от того, к какой части считать приложенной силу Р. Например, считая эту силу приложенной к телу АС, получим из условий равновесия левой части (рис.43, б):

Σ Х ^(АС) = 0; → X_C = – Р /2;

Σ Y ^(АС) = 0; → Y_C = - Р /2.

А если считать силу Р поделенной поровну между левой и правой частями рамы, то Y_C будет равняться нулю. В общем случае эту силу можно поделить в любом соотношении между частями рамы, но в сумме с реакцией Y_C она всегда будет равняться - Р /2.

Пример 22. Определить графически опорные реакции рамы, изображенной на рис.44.

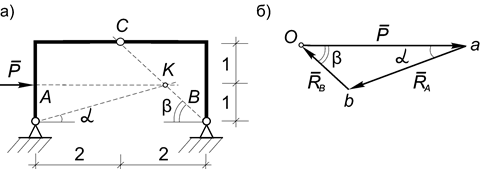
Рис.44

Решение. Система состоит из двух тел, имеющих равное число алгебраических неизвестных: 4 - для АС (X_A, Y_A, X_C, Y_C) и 4 - для ВС (X_B, Y_B, X_C ’, Y_C ’), но на тело АС действуют три силы (P, R_A, R_C), а на ВС - только две (R_В, R_C ’), поэтому начинаем решение с рассмотрения тела ВС.

Согласно второй аксиоме R_В и R_C ’ действуют вдоль прямой, соединяющей точки их приложения, то есть по прямой ВС.

Рассмотрим равновесие всей рамы АВС как твердого тела. На нее действует уравновешенная система трех непараллельных сил, которая в силу теоремы о трех силах должна быть сходящейся, поэтому реакция R_A должна проходить через точку К, где пересекаются линии действия R_В и R_C ’ (рис.44, а).

Строим силовой треугольник, проводя через начало и конец вектора Р прямые, параллельные направлениям R_A и R_В до их пересечения (рис.44, б).

Из подобия силового треугольника Oab и треугольника ВАК на чертеже находим искомые реакции:

R_В / P = (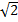)/4; → R_В = (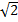)/4; X_В = - (R_В 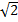)/2 = - P /4; Y_В = P /4.

| X_А |/ P = 3/4; X_А = -(3/4) P; Y_А = - P /4.

Пример 23. Определить графически опорные реакции рамы, показанной на рис.45.

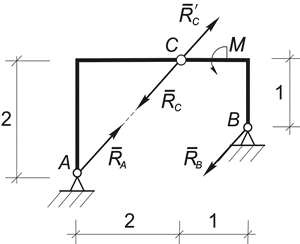
Рис.45

Решение. Начинаем рассмотрение с части, на которую действуют только две силы, и по аксиоме 2 определяем линию действия R_A (рис.45).

Рассматривая равновесие рамы в целом, приходим к заключению, что опорные реакции R_A и R_В должны составить пару, которая уравновесит приложенный к раме момент. Отсюда следует, что R_A = R_В = М / 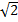, при этом

X_А = Y_А = R_A (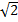 /2) = М /2; X_В = Y_В = - М /2.

Примечания к решению задач:

1. При решении задач с большим числом нагрузок – например, при выполнении расчетно-проектировочных работ все вычисления удобнее делать в десятичных дробях. В этом случае все результаты и проверка будут получаться с некоторым приближением, но относительная погрешность независимо от величин определяемых реакций и даже при использовании самых скромных вычислительных средств не должна выходить за пределы 1%.

2. Если проверка не выполняется и не удается найти ошибку, то нужно, во-первых, постараться ее локализовать, то есть выяснить, какие из вычисленных реакций найдены неверно, и воспользоваться для их определения альтернативными уравнениями. Во-вторых, можно воспользоваться следующим приемом, который вытекает из свойств систем линейных алгебраических уравнений: опорные реакции от заданной нагрузки равны сумме опорных реакций от каждой нагрузки в отдельности.

Дата добавления: 2015-06-04