Представление физических величин операторами

Как, зная волновую функцию предсказать результат измерения соответствующей физической величины у частицы, находящейся в рассматриваемом квантовом состоянии? Для получения информации о физических величинах, связанных с движущейся частицей, в квантовой механике разработан специальный математический аппарат, который использует представления об операторах физических величин и результатах их действия на волновые функции.

В работах М.Борна, П.Дирака и др. был сформулирован второй постулат квантовой механики, утверждающий, что каждой физической величине соответствует определенный оператор этой физической величины. При этом соотношения между операторами в квантовой механике имеют ту же структуру, что и соотношения между соответствующими им физическими величинами в классической механике.

Для расшифровки этого постулата дадим некоторые пояснения. Оператор - это математическое правило, следуя которому мы можем преобразовать одну функцию в другую. Задать оператор - это означает определить рецепт такого преобразования. Такое преобразование может быть простым умножением исходной функции на число или известную функцию, дифференцированием функции, перестановкой аргументов функции и др.

В квантовой механике в качестве символа соответствующего оператора используется классическое обозначение физической величины, ставя над буквой "шляпку" в виде значка " 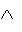". Например, - это оператор координаты 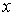, 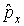- оператор проекции импульса на ось 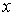, - оператор потенциальной энергии и т.д. Оператор предполагается действующим на написанную вслед за ним функцию. В качестве таких функций в квантовой механике выступают волновые функции. При этом равенство двух функций в операторной форме будет записываться как равенство операторов: .

Определим операторы основных физических величин в квантовой механике.

1. Оператор координаты. Действие этого оператора на волновую функцию сводится к умножению ее на соответствующую координату, то есть.

.

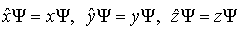(3.27)

В символической операторной форме записи этих операций имеют вид

.

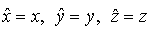(3.28)

Объединяя эти формулы, можно ввести векторный оператор , соответствующий радиусу-вектору в классической механике. Такой оператор формально рассматривается как некоторый вектор, имеющий в качестве компонент в декартовой системе координат операторы 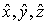. Поэтому

.

(3.29)

2. Оператор импульса. С помощью операций дифференцирования по координатам определим операторы проекций импульса, записав эти определения в символической операторной форме как

.

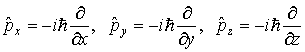(3.30)

Все три формулы в (3.30) можно объединить в одну, введя векторный оператор импульса , который с учетом (3.30) запишется как

.

(3.31)

Здесь

.

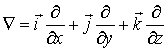Используя соотношение классической механики

,

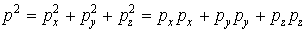определим оператор квадрата импульса как

.

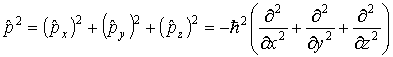(3.32)

Используя символ оператора Лапласа, запишем (3.32) в более компактном виде

.

(3.33)

3. Оператор момента импульса. По формуле классической механики, определяющей момент импульса частицы как вектор 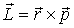, запишем выражения для его проекций на координатные оси:

.

Эти соотношения превратим в операторные, определяющие операторы проекций момента импульса

.

(3.34)

Оператор квадрата момента импульса можно построить по правилу

.

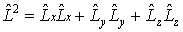(3.35)

Отметим, что задачи квантовой механики, обладающие сферической симметрией, удобнее решать не в декартовой, а в сферической системе координат , 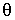и . Переходя от декартовых координат к сферическим по обычным правилам замены переменных 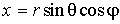, , 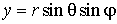, 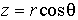формулы (3.34) и (3.35) можно преобразовать к следующему виду

.

(3.36)

Здесь

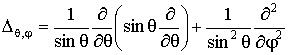
- угловая часть оператора Лапласа в сферической системе координат.

4. Операторы энергий. Классическая формула связи кинетической энергии частицы с квадратом ее импульса

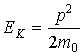
позволяет записать аналогичное соотношение между соответствующими операторами. Поэтому

.

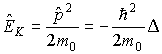(3.37)

Если частица движется в стационарном силовом поле, и ее потенциальная энергия определена в любой точке пространства, то оператор потенциальной энергии 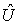определяется как оператор умножения на функцию , то есть

.

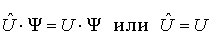(3.38)

Так как полная энергия частицы в классической механике есть сумма кинетической и потенциальной энергий, то в квантовой механике оператор полной энергии 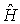определяется как сумма операторов кинетической и потенциальной энергий. Поэтому

.

Раскрывая выражение для оператора квадрата импульса по формуле (3.33), запишем оператор полной энергии как

.

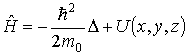(3.39)

В классической механике полную энергию частицы, выраженную через ее координаты и импульс, называют функцией Гамильтона. Поэтому в квантовой механике оператор полной энергии называют оператором функции Гамильтона или просто гамильтонианом.

Гамильтониан является основным оператором квантовой механики, поскольку, выбирая конкретный вид гамильтониана, с учетом силового поля, действующего на частицу, мы формулируем на математическом языке все особенности квантовой системы. Поэтому и основное уравнение нерелятивистской квантовой механики - уравнение Шредингера (3.8) может быть записано в операторной форме

,

(3.40)

содержащей гамильтониан .

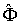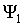Физическое содержание операторного метода в квантовой механике накладывает определенные ограничения на возможный вид квантовомеханических операторов. Пусть - оператор физической величины . Тогда для любых функций и и произвольных постоянных и должно выполняться равенство

.

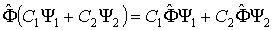(3.41)

Операторы, обладающие таким свойством, называются линейными операторами. Свойство линейности операторов физических величин тесно связано с принципом суперпозиции квантовых состояний. Только использование в теории линейных операторов не нарушает этого принципа.

Оператором физической величины может быть только линейный самосопряженный (эрмитов) оператор. Только такому оператору соответствует действительная (не комплексная) физическая величина. Самосопряженным называют оператор, который совпадает со своим сопряженным оператором. В этом случае для произвольных функци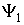й и 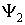тождественно выполняется следующее интегральное равенство

.

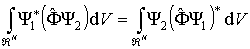(3.42)

Таким образом, каждой физической величине в квантовой механике приводится в соответствие определенный линейный самосопряженный оператор. Непосредственной проверкой можно убедиться, что все приведенные выше квантовомеханические операторы обладают такими свойствами.

8. Представление Шрёдингера — один из способов описания квантовомеханических явлений, предложенный Э. Шрёдингером в 1926 году. Здесь эволюция системы во времени описывается изменением вектора состояния, а операторы физических величин постоянны.

Оператор физической величины в представлении Шрёдингера:

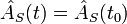
Вектор состояния в представлении Шрёдингера:

,

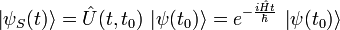где

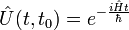§ — оператор эволюции;

§ — гамильтониан.

Соответственно, уравнение Шрёдингера имеет стандартный вид:

,

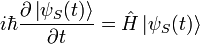Переход от представления Шрёдингера к представлению Гейзенберга

Рассмотрим случай, когда оператор Гамильтона не зависит от времени. Разложим произвольную волновую функцию по волновым функциям стационарных состояний .

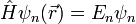— по определению стационарных состояний. — собственная энергия состояния .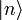

Тогда само разложение можно записать, как:

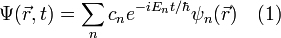
Введем унитарный оператор

Его собственные функции совпадают с собственными функциями оператора Гамильтона , то есть с функциями . Тогда обладает следующим свойством:

Используя этот оператор можно записать разложение 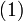в виде:

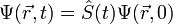
или, что то же самое:

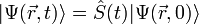
Эта запись означает, что оператор переводит состояние в начальный момент времени в состояние в произвольный момент времени.

Теперь для того, чтобы перевести зависимость от времени с волновой функции на произвольный оператор, мы рассмотрим среднее значение некого опер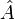атора :

— по определению среднего значения оператора.

Используя оператор 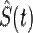и помня, что он унитарный, можно записать среднее значение оператора 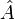, как:

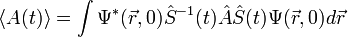— по определению среднего значения оператора.

Таким образом мы приходим к связи произвольного оператора в представлении Гейзенберга и представлении Шрёдингера:

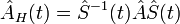
где — унитарный оператор, удволетворяющий условию .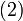

Для Гейзенберговского представления не применимо уравнение Шрёдингера. Вместо него в представлении Гейзенберга используется уравнение Гейзенберга для операторов:

9. Представление взаимодействия (представление Дирака) — один из способов описания квантовомеханических явлений, предложенный П. Дираком в 1927 году.

Запишем уравнение Шрёдингера в виде:

,

где

§ — гамильтониан невзаимодействующих полей (частиц);

§ — гамильтониан взаимодействия.

Введём вектор состояния:

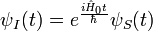
Тогда любой оператор можно записать в виде:

Таким образом, в представлении взаимодействия уравнение Шрёдингера примет вид:

15. Эквивале́нтная схе́ма (схема замещения, эквивалентная схема замещения) — электрическая схема, в которой все реальные элементы заменены максимально близкими по функциональности цепями из идеальных элементов.

Необходимость эквивалентных схем

Одной из основных задач электроники является расчет электрических схем, то есть получение детальной количественной информации о процессах, происходящих в этой схеме. Однако рассчитать произвольную схему, состоящую из реальных электронных компонент, практически невозможно. Мешает расчету то обстоятельство, что попросту не существует методик математического описания поведения реальных электронных компонент (например, транзистора) как единого целого. Имеются значения отдельных параметров и экспериментально снятые зависимости, но связать их в единую точную формулу, полностью описывающую поведение компоненты, в большинстве случаев не представляется возможным.

С другой стороны, исключительно простым математическим аппаратом описываются идеализированные базовые элементы электронных схем (например, идеальный резистор). Однако они не существуют в реальном мире. Так, любой резистор имеет множество паразитных параметров: индуктивность, емкость, температурные зависимости и т.п.

Введение понятия эквивалентная схема позволяет «связать» мир реальных компонент и мир их идеальных приближений. Эквивалентная схема представляет собой цепь только из идеальных компонент, которая функционирует примерно также, как и исходная схема. В эквивалентной схеме могут быть отражены, при необходимости, различные паразитные эффекты: утечки, внутренние сопротивления и т.д. Эквивалентная схема может составляться как для одного элемента, так и для сложной цепи.

[править]Идеальные элементы

В эквивалентных схемах используются перечисленные ниже идеальные элементы. Предполагается также, что геометрические размеры эквивалентной схемы настолько малы, что какие-либо эффекты длинных линий отсутствуют, то есть эквивалентная схема рассматривается каксистема с сосредоточенными параметрами.

§ Резистор. Идеальный резистор характеризуется только сопротивлением. Индуктивность, емкость, а также сопротивление выводов равны нулю.

§ Конденсатор. Идеальный конденсатор характеризуется только ёмкостью. Индуктивность, утечка, тангенс угла потерь, диэлектрическое поглощение а также сопротивление выводов равны нулю.

§ Катушка индуктивности. Идеальная катушка индуктивности характеризуется только индуктивностью. Емкость, сопротивление потерь, а также сопротивление выводов равны нулю.

§ Источник ЭДС. Идеальный источник ЭДС характеризуется только своим напряжением. Внутреннее сопротивление и сопротивление выводов равны нулю.

§ Источник тока. Идеальный источник тока характеризуется только своим током. Утечка равна нулю.

§ Проводники. Элементы эквивалентной схемы соединены идеальными проводниками, то есть индуктивность, емкость и сопротивление проводников равны нулю.

16. Размерные эффекты квантовой физики. Квантово-размерный эффект — эффект связанный с квантованием энергии носителей заряда, движение которых ограничено в одном, двух или трёх направлениях. При ограничении бесконечного кристалла потенциальными барьерами или при создании границ возникают дискретные уровни квантования. В принципе, дискретный спектр возникает в любом ограниченном потенциальными стенками объёме, но практически наблюдается только при достаточно малом размере тела, поскольку эффекты декогеренции приводят к уширению энергетических уровней, и поэтому энергетический спектр воспринимается как непрерывный. Поэтому наблюдение квантово-размерного эффекта возможно только если хотя бы один из размеров кристалла достаточно мал. Например, типичным примером квантово-размерного эффекта может служить двойная гетероструктура AlGaAs/GaAs/AlGaAs с двумерным электронным газом, где электроны находящиеся в слое GaAs ограничены высокими потенциальными барьерами AlGaAs, то есть для электронов формируется потенциальная яма, описываемая дном зон проводимостидвух материалов, малого размера (обычно порядка 10 нм) и возникают дискретные уровни, которые соответствуют движению электронов поперёк слоя GaAs, хотя продольное движение остаётся свободным. Эти уровни эффективно сдвигают зону проводимости вверх по энергии. В результате изменяется ширина запрещённой зоны GaAs и соответственно происходит сдвиг в синюю область края межзонного поглощения. Аналогично, но с большим изменением запрещённой зоны квантово-размерный эффект наблюдается в квантовых точках, где электрон ограничен по всем трём координатам.

[править]Принцип неопределённости

Энергия размерного квантования является следствием принципа неопределённости в квантовой механике. Если частица ограничена в пространстве в пределах расстояния L (допустим ограничен вдоль направления z), неопределённость z -компоненты ее импульса возрастает на величину порядка . Соответствующее увеличение кинетической энергии частицы дается выражением , где m ^* — эффективная масса частицы. Кроме увеличения минимальной энергии частицы квантовый размерный эффект приводит также к квантованию энергии её возбуждённых состояний. Энергии возбуждённых состояний для бесконечного одномерного потенциала прямоугольной ямы выражаются как E_n = Δ En ², где n = 1,2,3,…

17. Эффе́кт Ааро́нова — Бо́ма (иначе эффект Эренберга — Сидая — Ааронова — Бома) — квантовое явление, в котором на частицу с электрическим зарядом или магнитным моментом электромагнитное поле влияет даже в тех областях, где напряженность электрического поля E и индукция магнитного поля B равны нулю^[1], но не равны нулю скалярный и/или векторный потенциалы электромагнитного поля (то есть если не равен нулю электромагнитный потенциал).

Самая ранняя форма этого эффекта была предсказана Эренбергом и Сидаем в 1949 году^[2], подобный эффект был позже предсказан вновь Аароновым и Бомом в 1959 году^[3]. Эффект наблюдается для магнитного поля и электрического поля, но влияние магнитного поля зафиксировать легче, поэтому впервые эффект был зарегистрирован именно для него в 1960 году^[4]. Эти экспериментальные данные, однако, подвергались критике, поскольку в проведённых измерениях не удавалось в полной мере создать условия, при которых электрон совсем не проходил бы через области с ненулевой напряженностью магнитного поля. Все сомнения в существовании эффекта в экспериментах были сняты после проведения в 1986 году опытов с использованием сверхпроводящих материалов, полностью экранирующих магнитное поле (в смысле экранирования его вектора индукции)^[5].

Сущность эффектов Ааронова — Бома можно переформулировать так, что обычной для классической электродинамики^[6] концепции локального воздействия напряженности^[7] электромагнитного поля на частицу не достаточно, чтобы предсказать квантовомеханическое поведение частицы — на самом деле для этого оказалось необходимым, если исходить из напряженности, знать напряженность поля во всём пространстве.^[8] (Если E или B ненулевые хотя бы в какой-то области пространства, куда заряженная частица не может попасть (квантовая вероятность попасть туда исчезающе мала), тем не менее такое поле может заметно влиять на квантовое поведение такой частицы - то есть на вероятности попадания частицы в разные места той области пространства, которая ей доступна, дифракционная картина, в том числе положение дифракционного максимума итп).

Однако через электромагнитный потенциал теория эффекта строится естественно и локально.

Эффект Ааронова — Бома можно интерпретировать как доказательство того, что потенциалы электромагнитного поля (электромагнитный потенциал) являются не просто математической абстракцией, полезной для вычисления напряженностей, а в принципе независимо наблюдаемыми^[9] величинами, имеющими таким образом несомненный и прямой физический смысл.

18. Эффект Джозефсона — явление протекания сверхпроводящего тока через тонкий слой диэлектрика, разделяющий два сверхпроводника. Такой ток называют джозефсоновским током, а такое соединение сверхпроводников — джозефсоновским контактом. В первоначальной работе Джозефсона предполагалось, что толщина диэлектрического слоя много меньше длины сверхпроводящей когерентности, но последующие исследования показали, что эффект сохраняется в гораздо более широком классе контактов. Различают стационарный и нестационарный эффекты Джозефсона.

[править]Стационарный эффект

При пропускании через контакт тока, величина которого не превышает критическую, падение напряжения на контакте отсутствует (несмотря на наличие слоя диэлектрика). Эффект этот вызван тем, что электроны проводимости проходят через диэлектрик без сопротивления за счёттуннельного эффекта.

[править]Нестационарный эффект

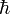При пропускании через контакт тока, величина которого превышает критическую, на контакте возникает падение напряжения U, и контакт при этом начинает излучать электромагнитные волны. При этом частота такого излучения определяется как , где — заряд электрона, — постоянная Планка.

Возникновение излучения связано с тем, что объединённые в пары электроны, создающие сверхпроводящий ток, при переходе через контакт приобретают избыточную по отношению к основному состоянию сверхпроводника энергию . Единственная возможность для пары электронов вернуться в основное состояние — это излучить квант электромагнитной энергии .

[править]Применение эффекта

Используя нестационарный эффект Джозефсона, можно измерять напряжение с очень высокой точностью.

Эффект Джозефсона используется в сверхпроводящих интерферометрах, содержащих два параллельных контакта Джозефсона. При этом сверхпроводящие токи, проходящие через контакт, могут интерферировать. Оказывается, что критический ток для такого соединения чрезвычайно сильно зависит от внешнего магнитного поля, что позволяет использовать устройство для очень точного измерения магнитных полей (МЭМС Гироскопы).

Если в переходе Джозефсона поддерживать постоянное напряжение, то в нём возникнут высокочастотные колебания. Этот эффект, называемый джозефсоновской генерацией, впервые наблюдали И.К. Янсон, В.М. Свистунов и И.М. Дмитренко. Возможен, конечно, и обратный процесс — джозефсоновское поглощение. Таким образом, джозефсоновский контакт можно использовать как генератор электромагнитных волн или как приёмник (эти генераторы и приёмники могут работать в диапазонах частот, не достижимых другими методами).

В длинном джозефсоновском переходе (ДДП) вдоль перехода может двигаться солитон (Джозефсоновский вихрь), перенося квант магнитного потока. Существуют и многосолитонные состояния, переносящие целое число квантов потока. Их движения описываются нелинейнымуравнением синус-Гордона. Такой джозефсоновский солитон подобен солитону Френкеля (число квантов потока сохраняется). Если изолирующий слой сделать неоднородным, то солитоны будут «цепляться» за неоднородности, и, чтобы сдвинуть их, придётся приложить достаточно большое внешнее напряжение. Таким образом, солитоны можно накапливать и пересылать вдоль перехода: естественно было бы попытаться использовать их для записи и передачи информации в системе большого числа связанных между собой ДДП (квантовый компьютер).

В конце 80-х годов в Японии был создан экспериментальный процессор на эффекте Джозефсона. Хотя 4-х разрядное АЛУ делало его неприменимым на практике, данное научное исследование было серьезным экспериментом, открывающим перспективы на будущее.

Эффект Холла
1. Электроны
2. Зонд
3. Магниты
4. Магнитное поле
5. Источник тока

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле B течёт электрический ток под действием напряжённости E. Магнитное поле будет отклонятьносители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости^[1] будет служить условие, что при этом электрон не начнёт двигаться поциклоиде.

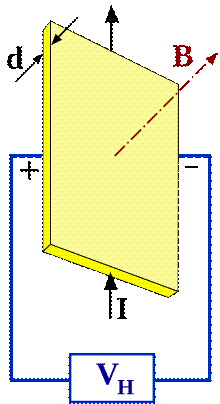
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска и положительного возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое полезарядов E ₁ не скомпенсирует магнитную составляющую силы Лоренца:

Скорость электронов v можно выразить через плотность тока:

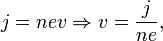
где n — концентрация носителей заряда. Тогда

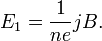
Коэффициент пропорциональности между E ₁ и jB называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак R_H, что объясняется в полуклассической и квантовой теориях твёрдого тела.

[править]Аномальный эффект Холла

Случай появления напряжения (электрического поля) в образце, перпендикулярного направлению пропускаемого через образец тока, наблюдающегося в отсутствие приложенного постоянного магнитного поля (то есть явление, полностью аналогичное эффекту Холла, но наблюдающееся без внешнего постоянного магнитного поля), называется аномальным эффектом Холла.

Необходимым условием для наблюдения аномального эффекта Холла является нарушение инвариантности по отношению к обращению времени в системе. Например, аномальный эффект Холла может наблюдаться в образцах снамагниченностью^[2].

[править]Квантовый эффект Холла

Основная статья: Квантовый эффект Холла

В сильных магнитных полях в плоском проводнике (то есть в квазидвумерном электронном газе) в системе начинают сказываться квантовые эффекты, что приводит к появлению квантового эффекта Холла: квантованию холловского сопротивления. В ещё более сильных магнитных полях проявляется дробный квантовый эффект Холла, который связан с кардинальной перестройкой внутренней структуры двумерной электронной жидкости.

[править]Спиновый эффект Холла

Основная статья: Спиновый эффект Холла

В случае отсутствия магнитного поля в немагнитных проводниках может наблюдаться отклонение носителей тока с противоположными направлениями спинов в разные стороны перпендикулярно электрическому полю. Это явление, получившее название спинового эффекта Холла, было теоретически предсказано Дьяконовым и Перелем в 1971 году. Говорят о внешнем и внутреннем спиновых эффектах. Первый из них связан со спин-зависимым рассеянием, а второй — со спин-орбитальным взаимодействием.

[править]Магнитосопротивление

Эдвин Холл проводил опыты в надежде обнаружить возрастание сопротивления проводника в магнитном поле, но в слабых полях не зарегистрировал его. Также оно не следует из теории металлов Друде, расчёты по которой приводились выше. Однако при более строгих расчётах и в сильных полях магнетосопротивление проявляется достаточно хорошо.

[править]Применение

Датчик Холла, используемый для измерения силы тока в проводнике. В отличие от трансформатора тока, измеряет также и постоянный ток.

Эффект Холла, в некоторых случаях, позволяет определить тип носителей заряда (электронный или дырочный) в металле или полупроводнике, что делает его достаточно хорошим методом исследования свойств полупроводников.

На основе эффекта Холла работают датчики Холла: приборы, измеряющие напряжённость магнитного поля. Датчики Холла получили очень большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя и выступают в роли ДПР (датчика положения ротора). ДПР реализует обратную связь по положению ротора, выполняет ту же функцию, что и коллектор в коллекторном ДПТ.

Также на основе эффекта Холла работают некоторые виды ионных реактивных двигателей.

эффект Казимира — эффект, заключающийся во взаимном притяжении проводящих незаряженных тел под действием квантовых флуктуаций в вакууме. Чаще всего речь идёт о двух параллельных незаряженных зеркальных поверхностях, размещённых на близком расстоянии, однако эффект Казимира существует и при более сложных геометриях. Причиной эффекта Казимира являются энергетические колебания физического вакуума из-за постоянного рождения и исчезновения в нём виртуальных частиц. Эффект был предсказан голландским физикомХендриком Казимиром (Hendrik Casimir, 1909—2000) в 1948 году, а позднее подтверждён экспериментально.

Дата добавления: 2015-06-04