Динамическая модель сошника

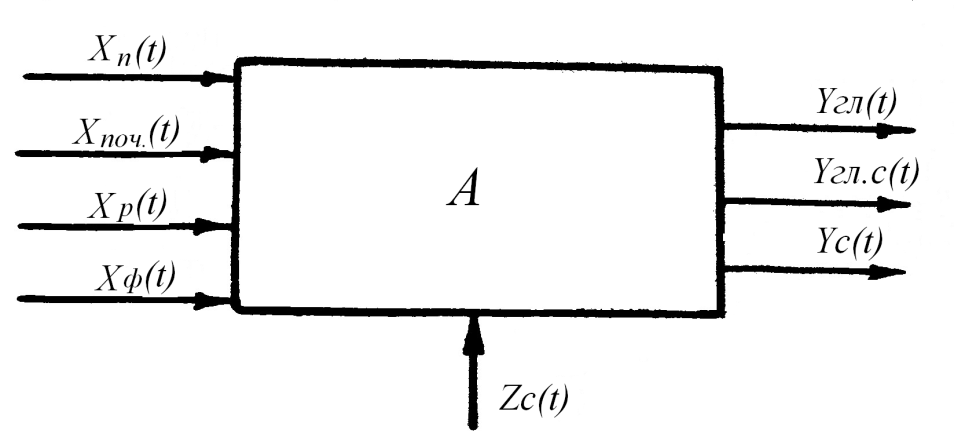
Внешние воздействия, нарушающие равновесие сошника, в предыдущем параграфе обозначены как f(t) - обобщенная функция внешних возмущений. Среди причин, вызывающих эти воздействия, отмечают обычно неровности поля (пусть это будет некоторая случайная функция X_n(t), изменения твердости почвы Х_поч(t), колебания рамы сеялки X_p(t), физические свойства почвы (влажность, липкость) X_ф(t).

В результате этих возмущений сошник меняет свое положение, а вместе с ним меняются показатели, характеризующие результаты его работы, например, угол колебания сошника У_гл(t), глубина заделки семян У_глс(t). Если сошник представить в виде прямоугольника А (рис. 9.8), то функции внешних возмущений X(t) можно изобразить как некоторые входы в динамическую систему, а функции, характеризующие качество работы, - выходы.

На работу сошников оказывает влияние и управление агрегата трактористом. Например, непрямолинейное движение может вызвать выглубление сошников. Пусть это воздействие будет обозначено Z(t) (рис. 9.8).

Таким образом, динамическая модель сошников представляет собой многомерную систему с названными входами и выходами (рис. 9.8).

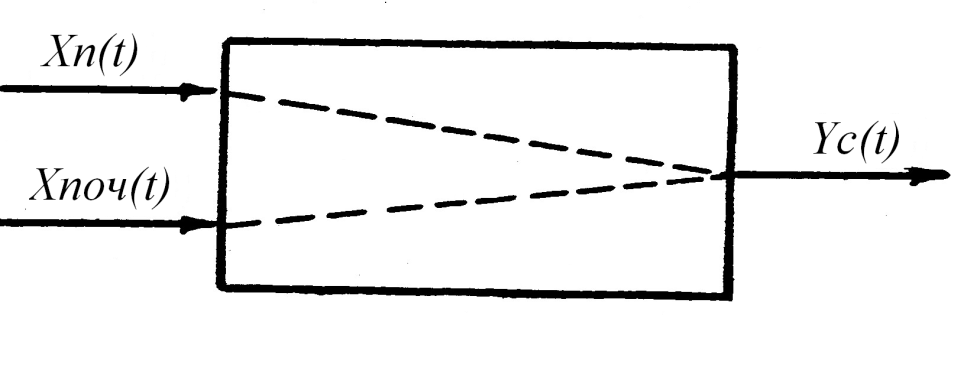
Разумеется, не все воздействия можно считать равноценными. Многочисленные исследования работы сеялок в условиях случайных возмущений [7] показали, что главными входными воздействиями, оказывающими влияние на сошник, являются неровности поверхности почвы и ее твердость. Определяющим выходным процессом, описывающим динамику сошника, является его колебание Y_c(t) (рис. 9.9).

Рис. 9.8. Динамическая модель сошника	Рис. 9.9. Двумерная модель сошника

Если учесть, что случайные процессы неровностей поверхности поля и продольной твердости почвы слабо коррелированы, а динамическая система сошника - линейна, то сложную модель можно разбить на простые, одномерные модели (рис. 9.10).

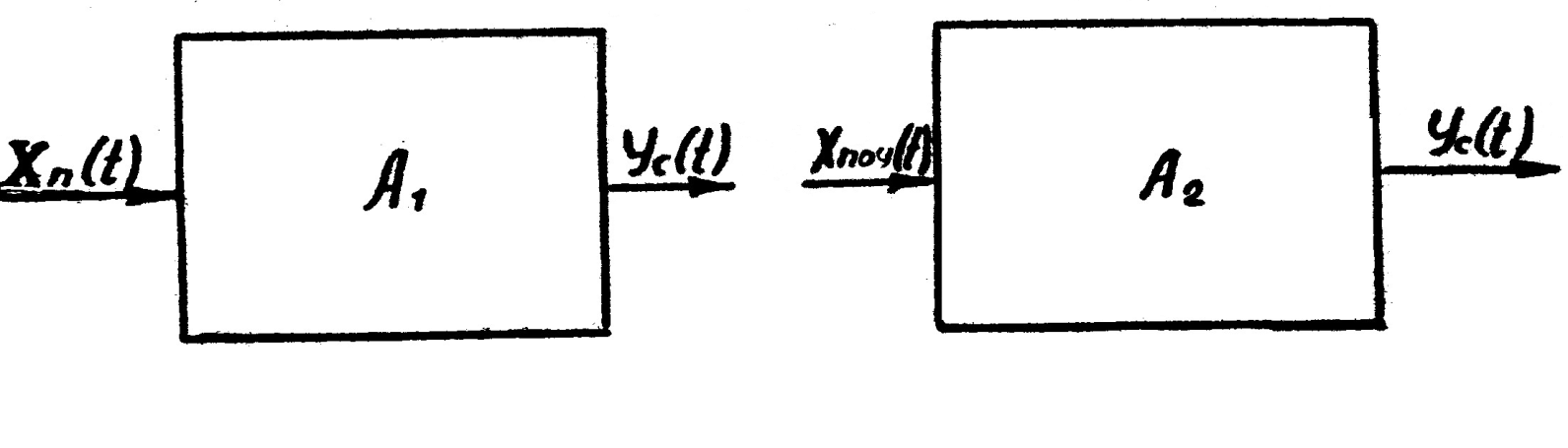
Рис. 9.10. Одномерные модели сошника

Результат одновременного воздействия указанных факторов на угол колебаний сошника (9.28) представить в терминах входа и выхода, то оно приобретает вид

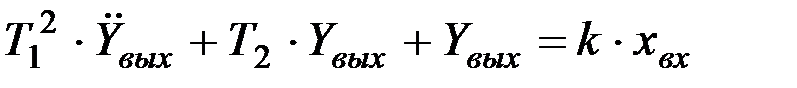. (9.29)

Да настоящего момента сошник рассматривался как некоторая самостоятельная динамическая система. Но он является лишь частью более сложной динамической системы сеялки и посевного агрегата в целом. Колебания сошника зависят от движения рамы сеялки. В свою очередь, сеялка колеблется около трактора, причем колебания можно рассматривать во всех ординатных плоскостях. Кроме этого, весь агрегат совершает сложное движение, копируя микрорельеф поля. Каждое из элементарных колебаний может быть описано дифференциальным уравнением, а сложная система, допустим с m обобщенными координатами y₁, y_2, y₃,...,y_m - системой дифференциальных уравнений:

,

,

,

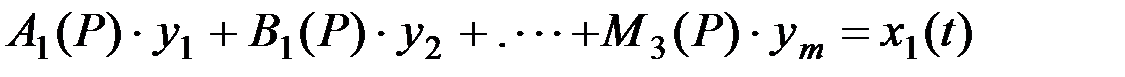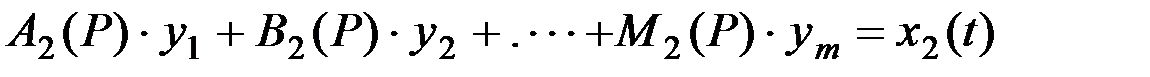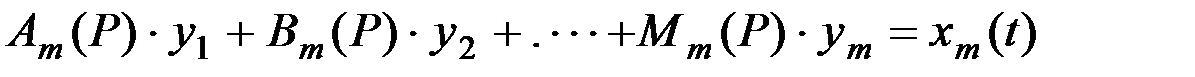где y₁, y₂...y_m - обобщенные координаты агрегата;

x₁(t); x₂(t)...x_m(t) - возмущающие воздействия;

A_i(P); B_i(P)...M_i(P) - дифференциальные полиномы.

Связь между входным воздействием и выходной величиной уравнений, что с математической точки зрения представляет собой достаточно сложную задачу.

Преодоление данной трудности обычно связывают с использованием методов операционного исчисления, в основе которых лежит использование интегрального преобразования Лапласа, -

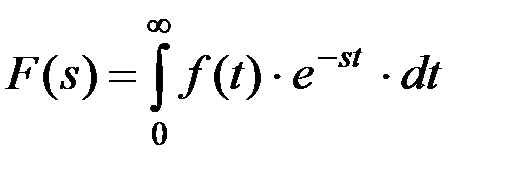, (9.31)

где S=α+iω - комплексное число;

f(t) - функция-оригинал;

F(S) - функция-изображение.

Идею операционного исчисления часто сравнивают с идеей логарифмирования, когда вместо действия над числами находят их логарифмы, проводят операции над ним, а затем по таблицам антилогарифмов определяют окончательный результат.

Если с помощью преобразования Лапласа (9.31) от функций, входящих в систему дифференциальных уравнений, перейти к функциям-изображениям F(S), то систему дифференциальных уравнений можно свести к системе обычных алгебраических уравнений, решить ее, а затем по таблицам обратных преобразований перейти от изображения к функциям-оригиналам.

В самом деле, если, например, известно изображение некоторой функции f(t):

,

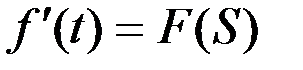то изображение производной от этой функции f¢(t) может быть найдено с помощью преобразования Лапласа (9.31):

.

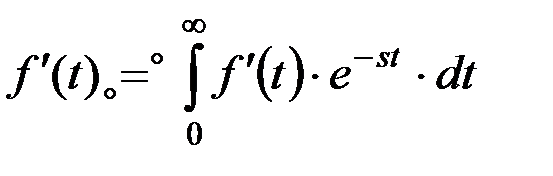Правую часть уравнения можно проинтегрировать по частям, используя известное соотношение:

.

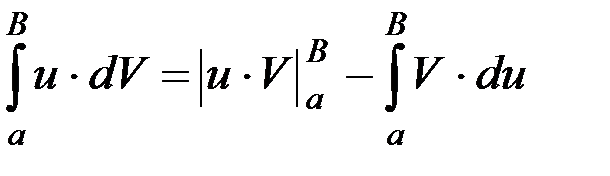Если

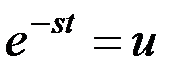, а ,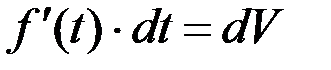

то

, ,

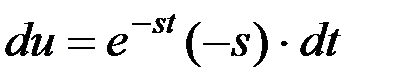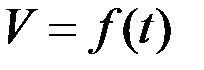тогда

,

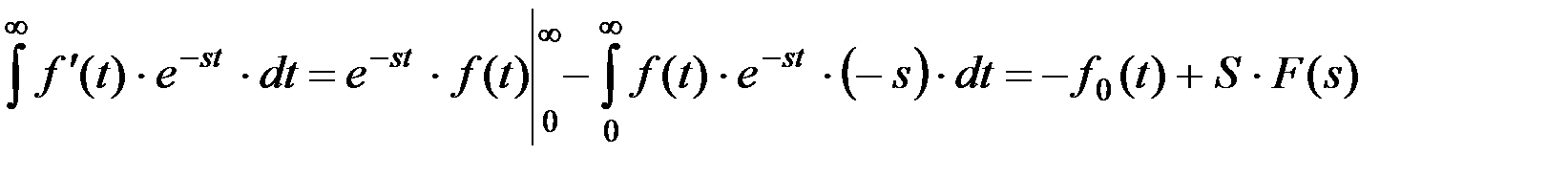где f₀(t) - значение функции при нулевых начальных условиях.

Итак,

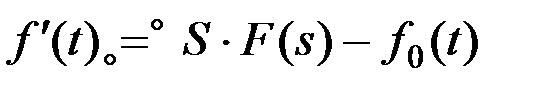. (9.32)

Иными словами, чтобы найти изображение производной, необходимо комплексный параметр S умножить на изображение самой функции и вычесть значение функции при начальных условиях.

Уравнение колебаний сошника (9.29) в преобразования Лапласа примет вид

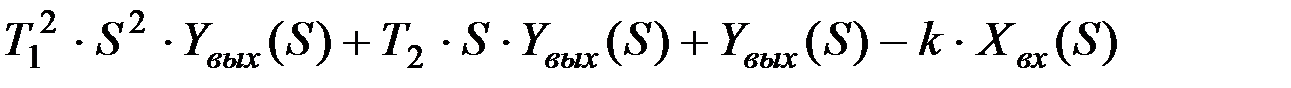, (9.33)

т.е. получено алгебраическое уравнение, не содержащее производных. Если Y_вых(S) в левой части уравнения вынести за скобки, то

,

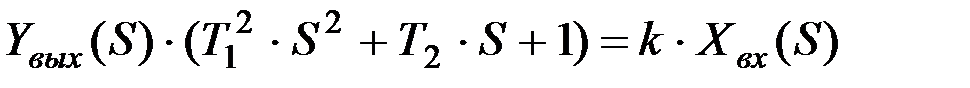отсюда

.

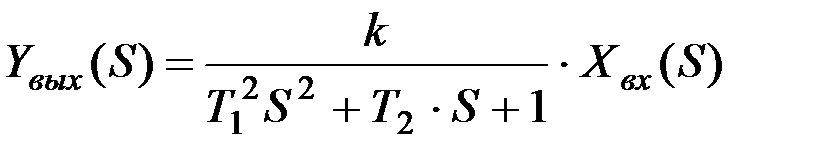Отношение преобразования Лапласа выходной величины к соответствующему входу представляет собой основную характеристику динамики механической системы - передаточную функцию W(S):

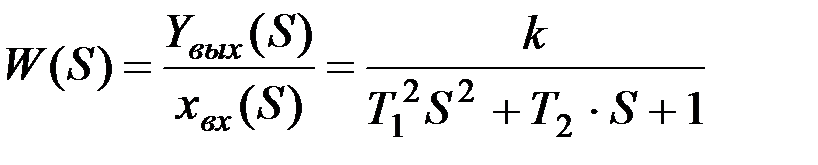. (9.34)

Сельскохозяйственные агрегаты и комплексы, как уже было отмечено, являются сложными динамическими системами, состоящими их отдельных узлов и элементов с различными связями, динамические свойства которых определяются соответствующими передаточными функциями. При определении передаточной функции всей системы возникает необходимость преобразования многозвеньевой схемы с целью ее упрощения или замены одним сложным звеном. Такие преобразования легко выполняются на структурных схемах.

Структурная схема динамической системы представляет собой графическое изображение системы в виде совокупности динамических звеньев с обозначением их передаточных функций и изображениями входных и выходных переменных (рис. 9.11).

Если динамическая система может быть представлена в виде цепи последовательных звеньев, то передаточная функция системы равна произведению передаточных функций звеньев:

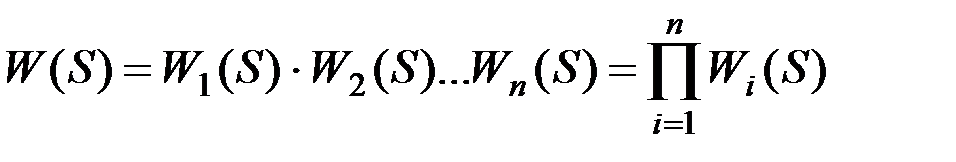. (9.35)

При параллельном соединении звеньев их передаточные функции алгебраически складываются:

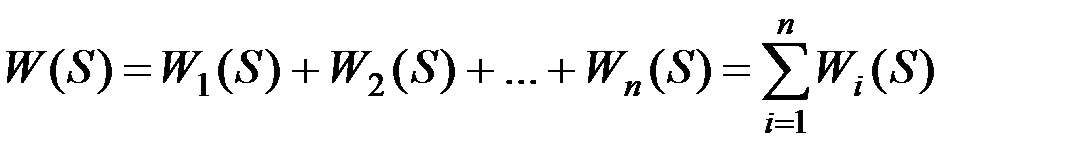(9.36)

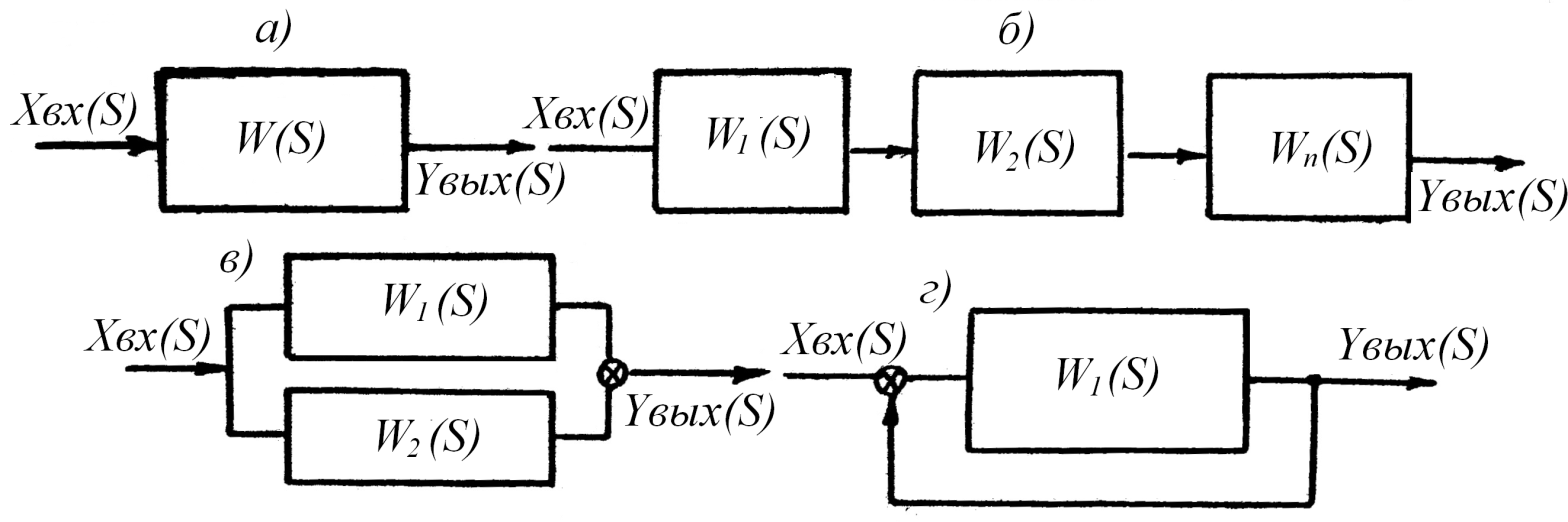
Рис. 9.11. Структурные схемы динамических систем: а - элементарное звено; б - последовательно соединенные звенья; в - параллельно соединенные звенья; г - звено, охваченное обратной связью

Для звеньев, охваченных обратной связью,

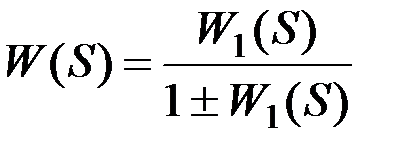, (9.37)

знак "плюс", берется при отрицательной обратной связи, а "минус" - при положительной.

Замена комплексного оператора S на произведение i×ω, где i - мнимая единица, а ω - угловая частота колебаний системы, приведет к появлению новой, а именно частотной характеристики динамической системы.

Если это произведение возвести в соответствующую степень, то в некоторых случаях i исчезнет, в других останется, так как i²=-1, i³=-i, i⁴=1 и т.д.

После группировки вещественных слагаемых и членов, содержащих мнимые величины, можно получить

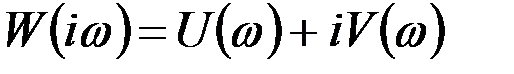. (9.38)

т.е. частотная функция представляет собой комплексное число. Пусть, например, передаточная функция имеет самый простой вид:

.

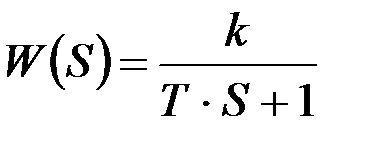После замены S на iω можно получить:

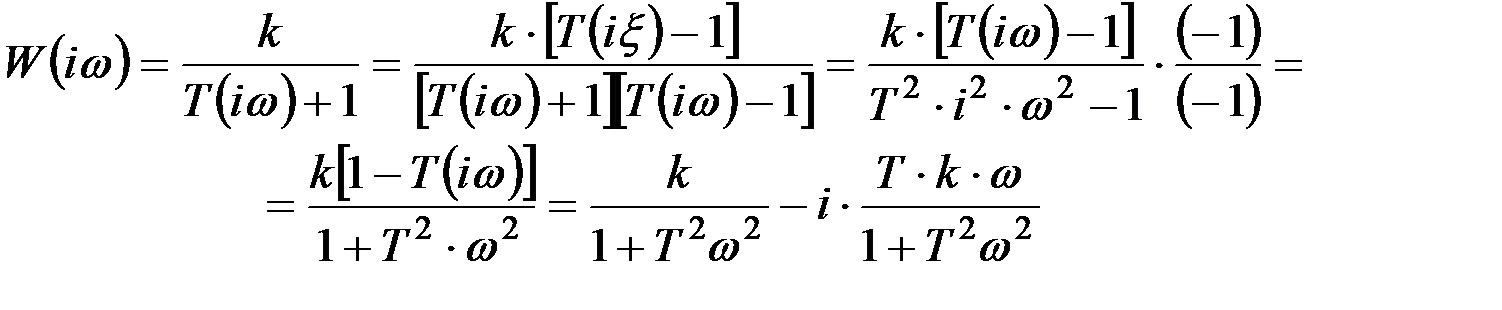
Если сравнить полученный результат с уравнением (9.8), то можно убедиться, что

; .

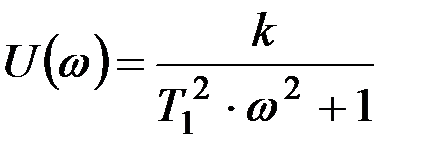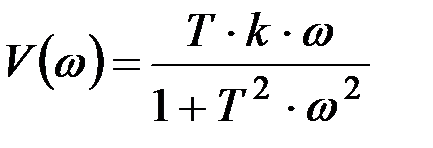Для каждого значения аргумента в диапазоне от ω=0 до ω=∞ можно вычислить значение W(iω), которое на комплексной области изобразит точку с координатами U(ω) и V(ω) (рис. 9.12). Длина вектора 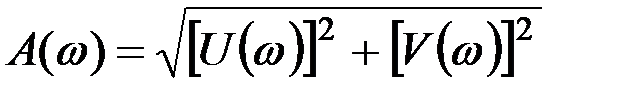называется модулем частотной характеристики, а

,

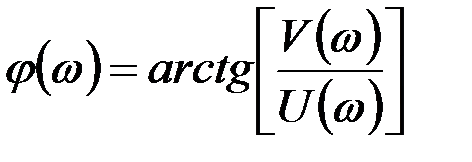углом сдвига фаз между входным воздействием и выходной величиной.

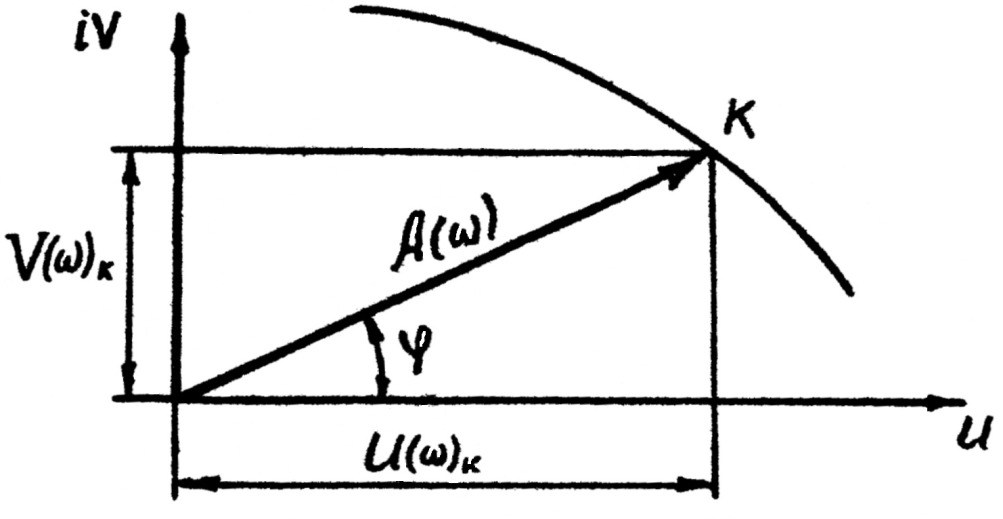
Рис. 9.12. Частотная характеристика динамической системы

При изменении ω новые значения примут А(ω) и φ(ω) так, что точка К опишет некоторую кривую (годограф), которая называется амплитудно-фазовой характеристикой.

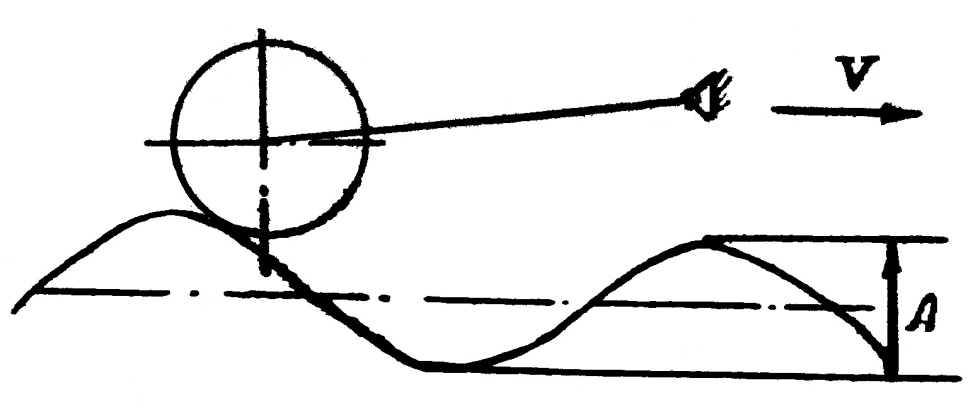
Частотная характеристика позволяет определить реакцию динамической системы на выходные возмущения в виде простых гармонических колебаний. Пусть, например, сошник сеялки перемещается по полю, поверхность которого представляет собой некоторую синусоиду с амплитудой А (на поле нарезаны гребни, рис. 9.13).

Если амплитуду колебаний обозначить а и рассмотреть соотношение а/А при различных значениях ω, то можно получить амплитудно-частотную характеристику (рис. 9.14).

Рис. 9.13. Движение сошника под воздействием гармонических колебаний	Рис. 9.14. Амплитудно-частотная характеристика

При малой скорости движения (ω≈0) траектория сошника повторит профиль поля и амплитуда его колебаний будет равна высоте гребней А, тогда а/А=1. Сдвига фаз между синусоидой профиля поля и углами колебаний сошника не будет, т.е. φ=0.

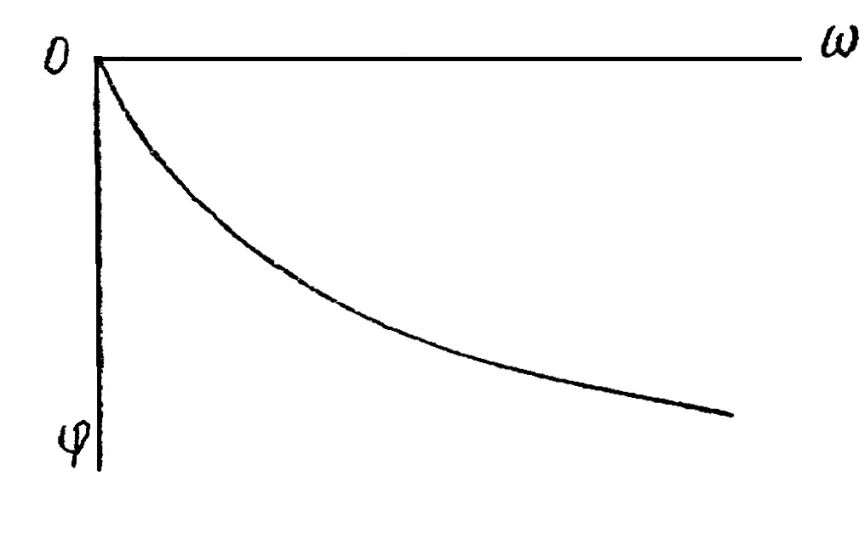
С ростом скорости амплитуда колебаний сошника может уменьшится, так как сошник не будет успевать полностью копировать профиль поля. Он может не опускаться до дна борозды и соотношение а/А будет уменьшаться, а угол сдвига фаз - увеличиваться. Если скорость движения машины возрастает до очень высокой величины, то сошник может вообще перестать копировать неровности поверхности поля. Если изобразить зависимость сдвига фаз от ω, то можно получить фазо-частотную характеристику.

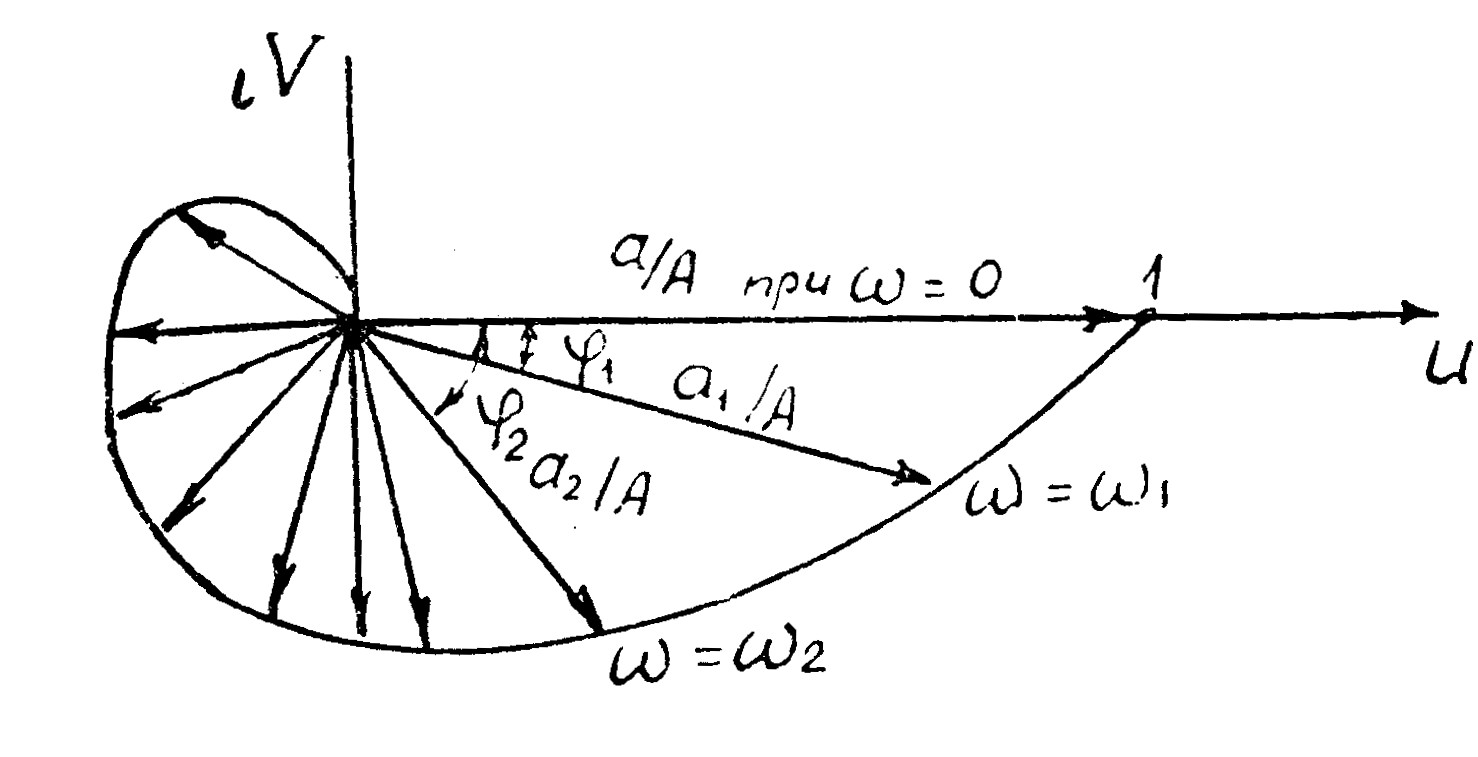
И наконец, эти характеристики могут быть обединены в амплитудно-фазовую на комплексной области.

Для описания реакции динамической системы на внешние скачкообразные возмущения используется так называемая временная характеристика системы h(t) (иногда в литературе ее называют разгонной характеристикой или переходной функцией).

Рис. 9.15. Фазо-частотная характеристика	Рис. 9.16. Амплитудно-фазовая характеристика

Представим себе, что перед сошником скачкообразно изменился профиль поля. Тогда, копируя поверхность, сошник перейдет с одного уровня на другой. Но вот способ перехода может оказаться разным. Тяжелый сошник, обладающей большой инерцией, может плавно перейти с одного уровня на другой (рис. 9.17а).

Звено с такой характеристикой называют апериодическим (или инерционным).

Сошник с другими механическим свойствами может перейти на новый уровень лишь после нескольких колебаний (рис. 9.17,б).

Анализ многочисленных механических систем с использованием методов статистической динамики показал, что несмотря на большое разнообразие конструкций, очень часто их динамические свойства определяются сравнительно небольшим набором передаточных, частотных и переходных функций. Это связано с тем, что в качестве исходных уравнений, описывающих движение механических систем, используются дифференциальные уравнения. Способов же составления этих уравнений не так много и, в конечно счете, все они базируются на использовании закона сохранения энергии.

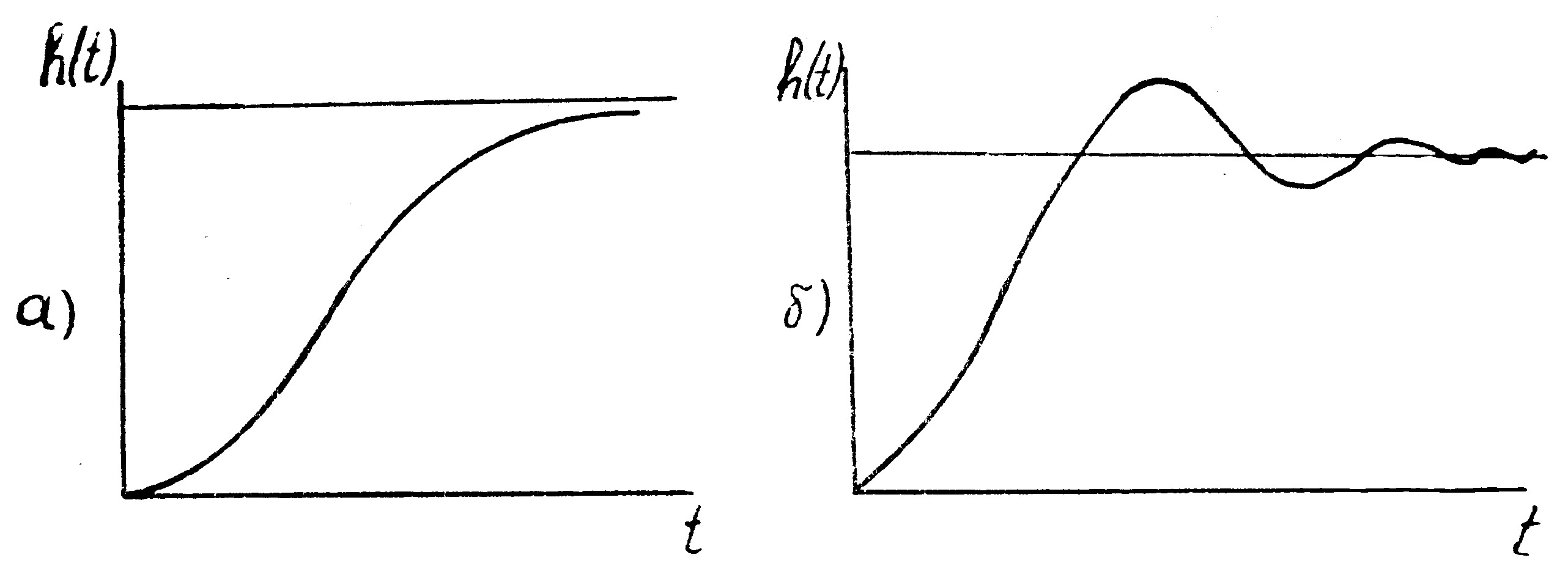
Рис. 9.17. Временная характеристика динамической системы.

Это дало возможность унифицировать динамические системы по их свойствам и свести их к так называемым типовым звеньям, среди которых чаще других используются безынерционные апериодические (инерционные), колебательные, дифференцирующие, интегрирующие звенья.

Исследования свойств сошниковых групп сеялок показали [6], что они относятся, главным образом, к апериодическим звеньям второго порядка и колебательным. Более того, апериодическое звено второго порядка и колебательное звено имеют вид передаточных функций (типа 9.34) и отличаются только соотношением инерционного Т₁ и демпфирующего Т₂ коэффициентов. Если Т₂≥2Т₁, то динамическая система будет представлять собой апериодическое звено (переходная функция изображена на рис. 9.17, а), а в случае, когда Т₂≤2Т₁ - колебательное (с переходной функцией рис. 9.17, б).

Качественная заделка семян возможна лишь тогда, когда сошник является апериодическим звеном и исключена возможность перехода системы в колебательный режим при каждом новом ее возмущении со стороны неровностей поля.

Определение значений коэффициентов передаточной функции на основе опытных данных составляет основную задачу при идентификации объектов исследований. В основе решения этой задачи лежит выявление закономерности преобразования входных возмущений X(t) динамическими системами А (рис. 9.10).

Дата добавления: 2015-06-04