Карты мира в цилиндрической проекции

Цилиндрические проекции применяются с эпохи Возрождения. Картографическая сетка в цилиндрических проекциях получается в результате проектирования поверхности глобуса на боковую по­верхность цилиндра (касательного или секущего). Затем боковая поверхность разрезается по боковой линии (образующей) и разво­рачивается в плоскость (рис. 57).

Разнообразие проекций зависит от взаимного расположения глобуса и цилиндра. При всем этом разнообразии ось цилиндра всегда проходит через центр глобуса. Цилиндрические проекции бывают прямые, поперечные, косые.

В прямых проекциях (наиболее употребительных) меридианы изображаются в виде параллельных прямых, а параллели — пря­мые линии, перпендикулярные меридианам. Расстояние между ли­ниями сетки вычисляется в миллиметрах.

При развертывании глобуса в прямой проекции:

а) экватор изображается прямой линией, по которой сохраня­ется главный масштаб о_экв = 1.00;

б) все параллели по длине равны экватору глобуса; чем боль­ше широта, т. е. ближе к полюсам, тем больше растягиваются па­раллели, тем большее по ним значение частного масштаба; его ве­личина пропорциональна секансу угла географической широты.

Значит, для того чтобы определить искажения, т. е. значение

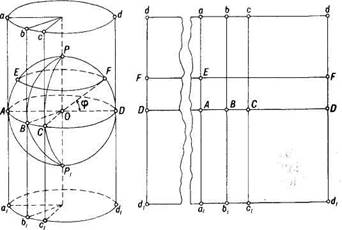
Рис. 57. Построение цилиндрической проекции (меридиан на глобусе РЕАР' изо# разился на карте как aEAa_t) ^: '"'''

изоколы частного масштаба по параллелям, необходимо по табли­цам определить величину секанса широты данной параллели. На­пример, sec 60° = 2.00, следовательно, параллель 60° с. ш. будет растянута в два раза на карте по сравнению с глобусом.

Ориентирование карт в цилиндрической проекции выполняется по линии север — юг, т. е. по меридиану.

Квадратная цилиндрическая проекция — это самая простая и легкая для построения проекция. Она вычислена португальскими мореплавателями в XV в.

Для объяснения школьникам сущности искажений на карте мож­но построить сетку параллелей и меридианов следующим образом: обернуть глобус бумажной полоской по экватору и наметить на ней черточками положение меридианов. На чистом листе бумаги прово­дим экватор как прямую линию и ставим метки пересечения эквато­ра меридианами. В этих местах перпендикулярно экватору проводим прямые линии — меридианы. На глобусе прикладываем полоску бу­маги к меридиану и отмечаем места пересечения его параллелями. Переносим эти метки на меридианы на бумагу и проводим параллели.

Таким образом картографическая сетка с помощью глобуса по­строена, и глобус развернулся в плоскость.

Проанализируем распределение искажений в этой проекции (что и определяет ее свойства):

1. Главный масштаб длин сохраняется по меридианам и по эк­ватору. Эллипс искажений на экваторе имеет форму окружности.

2. Главный масштаб площадей сохраняется вдоль линии экватора.

3. Частные масштабы по параллелям больше главного, т. е. па­раллели длиннее на карте по сравнению с их длиной на глобусе и все равны по длине экватору.

4. Увеличение длины параллелей по сравнению с глобусом про­исходит пропорционально широте: чем севернее параллель, тем боль­ше искажена ее длина. Например, параллель 60° увеличена в 2 раза.

5. Полюсы в прямой цилиндрической проекции не изображают­ся на карте.

6. Параллели и меридианы представляют собой взаимно пер­пендикулярные прямые линии.

7. По характеру искажений проекция равнопромежуточная (не изменилась длина меридианов).

Равноугольная цилиндрическая проекция Меркатора приме­няется для морских карт. В этой проекции сохраняется равенство углов, т. е. очертание контуров. Достигается это равномерным уве­личением длины меридианов соответственно увеличению длины па­раллелей (в квадратной проекции — напоминаем! — все меридиа­ны равны по длине и не искажены). Следовательно, по параллелям (кроме экватора) и меридианам масштабы частные. Они равны по всем направлениям, и эллипсы искажений в любом месте карты бу­дут представлять собой окружности.

Локсодромия в этой проекции — прямая линия, что позволяет

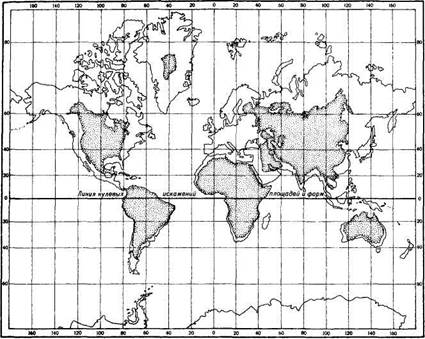
Рис. 58. Мировая карта в равноугольной нормальной цилиндрической проекции Меркатора

прокладывать курс судна по линейке, соединив две нужные точки по прямой. }

В проекции Меркатора сильно искажается (увеличивается) пло­щадь. Так, на картах в этой проекции Гренландия по площади поч­ти равна Африке, т. е. увеличена почти в 14 раз (рис. 58). Постро­ение сетки в проекции Меркатора производится на основе вычислений. Вычисляется расстояние от экватора до любой парал­лели по сложной формуле.

Поперечные цилиндрические проекции применяются для пост­роения топографических карт (см. раздел 4.2.2). Поперечный ци­линдр касается эллипсоида по меридиану. При этом изображаются полюса с осевым меридианом между ними. Сфероид проектируется на цилиндр по частям, представляющим собой шестиградусные зоны-двуугольники.

6.2.2. КАРТЫ РОССИИ В КОНИЧЕСКОЙ ПРОЕКЦИИ

Конические проекции начали использоваться в Древней Греции. В России они применены впервые в атласе Кириллова (1734). Используются конические проекции для изображения терри-

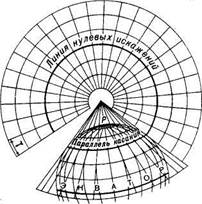
Рис. 59. Коническая проекция

торий, вытянутых по долготе и находящихся в средних широ­тах.

Сущность построения нор­мальных конических проекций заключается в том, что на бо­ковую поверхность конуса про­ектируются параллели и мери­дианы с поверхности глобуса. При этом ось конуса совпадает с осью глобуса, а конус касает­ся по одной (или двум, если он секущий) параллели, которая так и называется — параллель касания, она же линия нулевых искажений. Затем конус разре­зается по образующей и разво-

рачивается в плоскость. При этом картографическая сетка пред­ставляет собой трапеции, образованные меридианами — прямыми линиями, расходящимися под углом из вершины конуса, и парал­лелями — дугами концентрических окружностей с центром в вер­шине конуса (рис. 59).

Отметим, что угол у между меридианами на карте не равен раз­ности долгот (АХ), которые обозначены у меридианов, а может быть вычислен по формуле

у = Хс, с = sin ф₀,

где у — угол между меридианами на карте; X — разность долгот географических меридианов; с — коэффициент; ф₀ — широта па­раллели касания.

По характеру искажений конические проекции разделяются на равноугольные, равнопромежуточные, равновеликие.

Коническая проекция Птолемея строится на прямом касатель­ном конусе. Представив себе пространственную картину взаимного расположения фигур, перейдем к построению сетки проекции.

1. Задаются исходные данные для построения сетки, а именно масштаб карты, расстояние в градусах между параллелями (п°) и меридианами (т°), широта параллели касания (ф₀).

2. Вычисляется радиус параллели касания (в мм) по формуле

р = г ctg ф₀,

где г (мм) — радиус глобуса; ф₀— широта параллели касания.

3. Вычисляется расстояние между параллелями (а — отрезок меридиана — дуги большого круга) по формуле

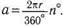
4. Расстояние между меридианами (Ь — отрезок параллели) определяется на параллели касания. Из таблиц известно значение Г дуги данной параллели (в км), его умножают на разность дол­гот между соседними меридианами (т°) и переводят в миллимет­ры, зная масштаб данной карты.

После этих вычислений приступают к построению проекции на листе бумаги.

1. Проводят меридиан симметрии. Для России принято считать таковым меридиан 100° в. д.

2. Вычисленным радиусом из вершины конуса, взятой на мери­диане симметрии произвольно, проводят параллель касания. Обыч­но широту выбирают так, чтобы параллель находилась посредине карты. Для России это может быть 55° с. ш.

3. По обе стороны от параллели касания на меридиане симме­трии откладывают отрезки — расстояния между параллелями. Са­ми дуги параллелей проводят из вершины конуса.

4. На параллели касания (не имеющей искажений на карте) от­кладывают отрезки b — расстояния между меридианами.

Внутренней рамкой ограничивают картографическое изображе­ние территории России или другой страны, затем строят градусную рамку, внешнюю рамку, и построение картографической сетки в проекции закончено.

Далее по координатам наносят очертания территории, контура и необходимые объекты, а также математические элементы: изоко-лы, эллипс искажений.

Свойства проекции Птолемея:

1. Главный масштаб сохраняется по всем меридианам и парал­лели касания.

2. Частные масштабы по другим параллелям больше главного.

3. Равноугольные и равновеликие свойства сохраняются вдоль параллели касания — линии нулевых искажений.

4. Искажения контуров, площадей возрастают по обе стороны от параллели касания. Причем в полосе 15° по обе стороны от нее они небольшие, далее к северу нарастают более значительно, чем к югу.

В 1931 г. для карт СССР была разработана нормальная кони­ческая проекция В. В. Каврайского. Она применялась для «Атла­са СССР» (7 класс), «Большого советского атласа мира». Проек­ция разработана Каврайским с расчетом наименьших искажений длин по меридианам и параллелям для территории СССР к югу от полярного круга. К северу от него качество изображения в расчет не принималось (рис. 60).

Проекция построена на секущем конусе и имеет две параллели касания, а именно 47° с. ш. и 62° с. ш., наибольшие искажения уг­лов около 0,5°. В этой проекции имеются линии нулевых искаже­ний всех видов. По всем меридианам масштаб главный, по парал­лелям касания также. При работе школьников или студентов с картами в этой проекции можно пользоваться транспортиром для измерения углов.

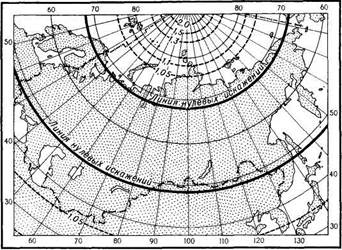
Рис. 60. Сетка в проекции Каврайского

В проекции Каврайского издана в 1949 г. Гипсометрическая карта СССР в масштабе 1:2 500 000.

С 50-х гг. для карт СССР применяется нормальная равнопро-межуточная проекция Ф. И. Красовского. Принцип ее построе­ния похож на построение проекции Каврайского: для расчетов ис­пользован тот же секущий конус, но введено условие сохранения площади заданного пояса и равенства масштабов длин по его край­ним параллелям —39°48' с. ш. и 73°30' с. ш., т. е. раздвинута по­лоса между параллелями касания, в пределах которой можно вы-

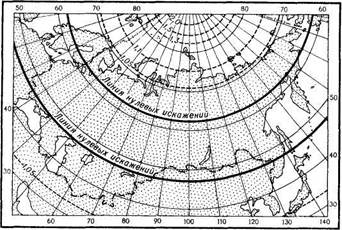
Рис. 61. Сетка в проекции Красовского

поднять картометрические работы, не внося поправки на искаже­ния (рис. 61).

Недостаток нормальных конических проекций состоит в том, что на касательном конусе главный масштаб сохраняется только по па­раллели касания, в остальных местах имеются искажения. На се­кущем конусе восточные и западные территории сильно разверну­ты, полюс находится за пределами изображения.

Чтобы сохранить масштаб на всех параллелях, необходимо градусную сетку строить с помощью множества конусов, а именно каждую параллель — на своем. Тогда каждая параллель ста­нет параллелью касания (радиус ее вычисляется по формуле Пто-. лемея: р = г ctg cp₀) и изобразится без искажений. Далее найти на параллелях, пользуясь таблицей длин дуг в Г, точки прохождения меридианов и провести их как сложные кривые, соединяя точки прохождения меридианов на соседних параллелях. Таков принцип построения картографической сетки в поликонических проекциях.

Дата добавления: 2015-06-04