
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Многие случайные события обладают свойством так называемой статистической устойчивости частот, о чем мы упоминали ранее. Выясним более подробно суть этого свойства
|
|
|
|
Случай, случайность — с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находка, случайная ошибка. Этот ряд можно продолжать бесконечно. Казалось бы, тут нет места для математики — какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности — они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
И перестановки, и размещения могут быть с повторениями. Имеет смысл говорить и о сочетаниях с повторениями. Из множества, содержащего предметов, возьмем один произвольный, занесем его в список, после чего вернем обратно. Затем точно так же выберем еще один объект и т. д., пока в списке не окажется наименований (среди них могут быть и одинако-вые). Принципиальное отличие от размещений с повторениями заключается в том, что в данном случае элементы списка не нумеруются. Например, списки «А, Б, А, Г» и «Б, Г, А, А» считаются одинаковыми. Попробуем найти число сочетаний с повторениями из элементов по.
Для этого придется проявить определенную изобретательность. Следите внимательно.
Произвольно пронумеруем элементы исходного множества числами от 1 до  . Пусть в какое-то из полученных сочетаний вошло
. Пусть в какое-то из полученных сочетаний вошло  , элементов под номером 1,
, элементов под номером 1, 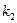 элементов под номером 2,...,
элементов под номером 2,...,  элементов под номером
элементов под номером  . Что можно сказать обо всех этих числах
. Что можно сказать обо всех этих числах 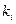 ? Ясно, что сумма
? Ясно, что сумма 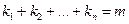 (ведь в списке всего
(ведь в списке всего  объектов!).
объектов!).
Теперь изобразим это сочетание в виде цепочки из нулей и единиц. Единица здесь будет обозначать каждый отдельный элемент сочетания, а нуль — символизировать границу между группами элементов, соответствующих соседним 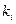 . Если некоторое
. Если некоторое  , т. е. элементов с номером
, т. е. элементов с номером 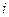 в списке нет, то в соответствующем месте цепочки окажутся два «пограничных» нуля подряд.
в списке нет, то в соответствующем месте цепочки окажутся два «пограничных» нуля подряд.
|
|
|
Итак, записываем: сначала  единиц, затем один нуль, после этого
единиц, затем один нуль, после этого 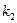 единиц и снова нуль...,
единиц и снова нуль...,  единиц и опять нуль, наконец,
единиц и опять нуль, наконец,  единиц – и все.
единиц – и все.
Поскольку сумма всех 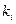 равна
равна  , в построенной цепочке содержится
, в построенной цепочке содержится  единиц. Нулей же
единиц. Нулей же 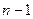 . Так что вся цепочка состоит из
. Так что вся цепочка состоит из  цифр.
цифр.
Подведем итог. Каждому возможному списку поставлена в соответствие некоторая цепочка из нулей и единиц длиной  . При этом если два списка одинаковы, то и цепочки получатся одинаковыми. Верно и обратное — каждой цепочке соответствует определенный список. Например, цепочка 1111001010 говорит нам, что в списке — четыре элемента номер 1, ни одного элемента номер 2, по одному элементу номер 3 и 4 и ни одного элемента номер 5. Таким образом, задача свелась к поиску ответа на вопрос: сколько можно составить различных цепочек длиной
. При этом если два списка одинаковы, то и цепочки получатся одинаковыми. Верно и обратное — каждой цепочке соответствует определенный список. Например, цепочка 1111001010 говорит нам, что в списке — четыре элемента номер 1, ни одного элемента номер 2, по одному элементу номер 3 и 4 и ни одного элемента номер 5. Таким образом, задача свелась к поиску ответа на вопрос: сколько можно составить различных цепочек длиной  из
из  единиц и
единиц и 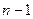 нулей? А это не что иное, как число перестановок с повторениями из
нулей? А это не что иное, как число перестановок с повторениями из  нулей и
нулей и 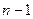 единиц, т. е.
единиц, т. е.  . Поэтому
. Поэтому
 (1.10)
(1.10)
Итак, формулы для перестановок, размещений и сочетаний (с повторениями и без) обнаруживают тесную связь между основными понятиями комбинаторики. Эти формулы составляют своего рода азбуку комбинаторики, поскольку на них основано решение не только большинства комбинаторных задач, но и задач по теории вероятностей, к рассмотрению которой мы приступаем.
Глава 1.6. Понятие вероятности события
Но прежде чем рассказать о закономерностях случайности, попытаемся ответить на вопрос: что такое азартная игра? Уверены, что большинство считают — это игра на деньги. Неверно. На деньги можно играть и в теннис, и в шахматы. Теннисисты и шахматисты получают большие гонорары за выигрыши в турнирах. А вот карты — азартная игра. Почему? Потому, что в ней главную роль играет случай — от него зависит, какие именно карты окажутся у партнеров. Правда, и в картежной игре умение игрока значит много. Но есть игры, в которых от игроков не требуется никакого умения. Например, «орлянка»: монету подбрасывают, и в зависимости от того, какой стороной она упала, выигрывает первый или второй партнер. Или другая игра, где властвует случай, — игра в кости. Остановимся на ней подробнее: именно с нее математики начали изучать его величество Случай.
|
|
|
Игральная кость, непременный атрибут многих настольных игр, — маленький кубик (гексаэдр), грани которого помечены цифрами или точками. Раньше такие кубики делали из кости, откуда и пошло их название — «игральные кости». Когда игральную кость бросают, то на ее верхней грани оказывается какое-то чисто от 1 до 6, по числу граней.
Игр в кости великое множество. Простейшая из них такова: двое по очереди бросают кубик. Выигрывает тот из них, кто «выкинул» большее число. Выигрыш может равняться или заранее назначенной сумме, или разности числа очков, выпавших на кубике при бросаниях. Часто бросают не один, а два, три или четыре кубика. Естественно, всякий игрок желает, чтобы у него чаще выпадала шестерка, поэтому многие игры в кости основаны на появлении именно шестерки.
Проследим, как выпадает шестерка при бросании кубика. Предположим, что кубик совершенно правильный — все его грани абсолютно одинаковы. Если подбрасывать кубик десять раз, то числа могут выпадать, например, в такой очередности: 1, 5, 2, 2, 3, 4, 1, 6, 3, 5 или в такой: 6, 5, 6, 3, 1, 1, 4, 2, 3, 6. В первом случае шестерка выпала один раз, а во втором — три раза. Может случиться, что шестерка не выпадет ни разу или все десять раз.
А если подбрасывать кубик не десять, а десять тысяч раз? Тогда каждая из граней будет выпадать примерно одинаково часто. Что это значит? Пусть 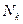 — количество выпадений грани при
— количество выпадений грани при  бросаниях кубика, тогда отношение
бросаниях кубика, тогда отношение 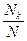 , которое называется частотой выпадения грани с цифрой
, которое называется частотой выпадения грани с цифрой  , будет приблизительно одинаково для всех граней кубика. Поскольку
, будет приблизительно одинаково для всех граней кубика. Поскольку

то все частоты будут близки к 1/6. Сама величина 1/6 называется вероятностью выпадения, как шестерки, так и пятерки, четверки и т. д.
Итак, мы получили формулу частоты выпадения грани с цифрой  , которую часто обозначают буквой
, которую часто обозначают буквой  (ню):
(ню):
 . (1.11)
. (1.11)
Если же подбрасывать монету, то вероятности выпадения и орла, и решки равны 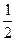 . Чуть позже мы дадим более строгое определение вероятности события. Слово «событие» в быту применяют к значительным явлениям, а в математике — ко всем возможным исходам рассматриваемой ситуации. Так, в случае бросания игральной кости событие — это выпадение той или иной грани. События будем обозначать большими латинскими буквами: например, появление 6 при бросании кости — через А, одного из чисел от 4 до 6 — через В, одного из чисел от 1 до 5 — через С. Вероятность произвольного события
. Чуть позже мы дадим более строгое определение вероятности события. Слово «событие» в быту применяют к значительным явлениям, а в математике — ко всем возможным исходам рассматриваемой ситуации. Так, в случае бросания игральной кости событие — это выпадение той или иной грани. События будем обозначать большими латинскими буквами: например, появление 6 при бросании кости — через А, одного из чисел от 4 до 6 — через В, одного из чисел от 1 до 5 — через С. Вероятность произвольного события  будем обозначать через
будем обозначать через  .
.
|
|
|
Впервые вероятности случайных событий в азартных играх вычислили в XVII в. французские математики Блез Паскаль и Пьер Ферма. Они подсчитывали число шансов (от фр. chance — «удача», «случай») события из общего возможного числа равновероятных исходов. Проследим за их рассуждениями.
Исход какого-либо испытания, опыта или игры, выражающийся в событии  , назовем шансом события
, назовем шансом события  (или благоприятствующим исходом события
(или благоприятствующим исходом события  ). Например, при бросании игральной кости возможны шесть равновероятных исходов
). Например, при бросании игральной кости возможны шесть равновероятных исходов 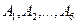 — выпадение 1, 2,..., 6 очков. Пусть событие
— выпадение 1, 2,..., 6 очков. Пусть событие  означает выпадение четного числа очков, т. е. 2, 4 или 6. В этом случае
означает выпадение четного числа очков, т. е. 2, 4 или 6. В этом случае 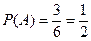 , т. е. вероятность
, т. е. вероятность  равна отношению числа шансов (благоприятствующих исходов) события
равна отношению числа шансов (благоприятствующих исходов) события  к общему числу равновероятных исходов. Такое определение называется классическим определением вероятности.
к общему числу равновероятных исходов. Такое определение называется классическим определением вероятности.
Итак, если при каких-либо условиях имеются  равновероятных исходов и
равновероятных исходов и  из них приводят к событию
из них приводят к событию  , то вероятность
, то вероятность  события
события  равна отношению
равна отношению 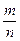 , т. е.
, т. е.
 . (1.12)
. (1.12)
В простых случаях вычислить вероятности не составляет труда. Например, подбросив вверх монету, мы знаем, что выпадет или орел, или решка. Пусть событие А означает появление орла. В подобных случаях будем впредь писать  = [появление орла]. Понятно, что
= [появление орла]. Понятно, что 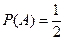 .
.
Хорошо перетасуем колоду из 36 карт и случайно вынем 1 карту. События  = [вынута карта червонной масти] и
= [вынута карта червонной масти] и 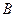 = [вынут туз] из 36 исходов имеют соответственно 9 и 4 шансов. Поэтому
= [вынут туз] из 36 исходов имеют соответственно 9 и 4 шансов. Поэтому  ,
, 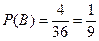 .
.
Рассмотрим следующую задачу. Среди 100 подрамников имеются 5 с дефектами. Какова вероятность того, что выбранные менеджером на удачу три подрамника окажутся без дефектов?
|
|
|
Рассуждаем следующим образом: из 100 подрамников три можно выбрать 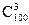 способами. Три без дефектов из общего числа 95 без дефектных можно выбрать
способами. Три без дефектов из общего числа 95 без дефектных можно выбрать  способами. Тогда по равенству 1.11 получаем, что
способами. Тогда по равенству 1.11 получаем, что
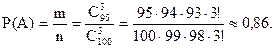
Таким образом, вычислить вероятность стало возможным благодаря тому, что вам известно, что такое сочетание.
Теорию вероятностей нередко называют «наукой о случайном». На многих примерах можно убедиться в том, что массовые случайные явления тоже имеют свои закономерности, знание которых можно успешно использовать в практической деятельности человека. Как наука, теория вероятностей зародилась в XVII в. Возникновение понятия вероятности было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр. Слово «азарт», под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова hasard буквально означающего «случай», «риск».
Азартные игры практиковались в ту пору, главным образом, среди знати, феодалов и дворян. Особенно распространенной была игра в кости, о чем мы говорили ранее.
С чем связано такое определение вероятности наступления события, которое мы выразили формулой (1.12)? Оказывается, что это обозначение не случайно. Дело в том, что  — начальная буква французское слова Probabilite — вероятность,
— начальная буква французское слова Probabilite — вероятность,  — слова Accident — случайность, происшествие. Вот почему мы и обозначаем вероятность наступления события таким видом:
— слова Accident — случайность, происшествие. Вот почему мы и обозначаем вероятность наступления события таким видом:  .
.
Все происходящие события можно классифицировать на три группы:
· которые не наступят ни при каких условиях, их называют невозможными;
· события, которые обязательно наступят в результате данного испытания, их называют достоверными;
· события, которые могут как наступить, так и не наступить в результате данного испытания, их называют случайными.
Очевидно, что вероятность невозможного события равна нулю. Вероятность достоверного события равна единице. А вероятность случайного события больше нуля, но меньше единицы, т.е.
 . (1.13)
. (1.13)
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие.
Как мы уже сказали, Ферма и Паскаль стали основателями математической теории вероятностей. Постепенное формирование интереса к задачам, связанным с вероятностями, происходило, прежде всего, под влиянием развития страхового дела, но те частные вопросы, которые побудили больших математиков поразмыслить над этим предметом, были поставлены в связи с играми в кости и в карты. Как выразился Пуассон, «задача, относившаяся к азартным играм и поставленная перед суровым янсенистом светским человеком, была источником теории вероятностей». Этим светским человеком был кавалер де Мере, который обратился к Паскалю с вопросом по поводу так называемой «задачи об очках». Паскаль завязал переписку с Ферма по поводу этой задачи и родственных вопросов, и они вдвоем установили некоторые из основных положений теории вероятностей (1654 г.).
Кавалер де Мере, один из французских придворных, был азартным игроком. Денежный выигрыш при игре в кости обычно зависит от комбинации выпавших чисел, на которую делается ставка. Одна их таких комбинаций — выпадение хотя бы одной шестерки при четырех бросаниях игральной кости. Де Мере смог подсчитать число шансов этой комбинации.
Общее число исходов при четырех бросаниях игральной кости равно 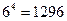 . Число шансов появления хотя бы одной шестерки составляет
. Число шансов появления хотя бы одной шестерки составляет 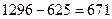 , так как шестерка не выпадает ни разу в
, так как шестерка не выпадает ни разу в  случаях. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях равна
случаях. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях равна 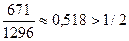 , поэтому при четырех бросаниях выгоднее делать ставку на то, что выпадет хотя бы одна шестерка, чем на то, что не выпадет ни одной. По-видимому, многие опытные игроки знали, что первая комбинация появляется чаше, чем вторая, и найти партнера на такую игру было трудно.
, поэтому при четырех бросаниях выгоднее делать ставку на то, что выпадет хотя бы одна шестерка, чем на то, что не выпадет ни одной. По-видимому, многие опытные игроки знали, что первая комбинация появляется чаше, чем вторая, и найти партнера на такую игру было трудно.
Более сложные комбинации возникали, если бросали сразу две кости. Де Мере пытался определить, сколько раз надо бросать пару костей, чтобы вероятность хотя бы одного появления двух шестерок была больше 1/2. Он подсчитал, что достаточно 24 бросаний. Однако опыт игрока заставил де Мере сомневаться в правильности своих вычислений. Тогда он обратился с этой задачей к математику Блезу Паскалю, который предложил правильное решение. Ученый определил, что при 24 бросаниях пары костей две шестерки появляются хотя бы раз с вероятностью, меньшей 1/2, а при 25 бросаниях — с вероятностью, большей 1/2.
В самом деле, если бросить один раз пару костей, две шестерки выпадут с вероятностью  , а не выпадут — с вероятностью
, а не выпадут — с вероятностью 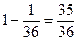 . При
. При  бросаниях пары костей число шансов непоявления пары шестерок равно
бросаниях пары костей число шансов непоявления пары шестерок равно  , а общее число исходов составит
, а общее число исходов составит  .
.
Обозначим события:
 = [хотя бы раз выпадет пара шестерок],
= [хотя бы раз выпадет пара шестерок],
 = [пара шестерок не выпадет ни разу].
= [пара шестерок не выпадет ни разу].
Тогда  ,
,  , откуда следует, что
, откуда следует, что 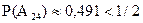 ,
, 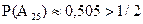 .
.
Решение порой довольно сложных задач, с которыми обращались заинтересованные лица к Паскалю, Ферма, Гюйгенсу, способствовало разработке основных понятий и общих принципов теории вероятностей, в том числе и правил действия над ними. Но это не означает, что основоположники теории вероятностей рассматривали азартные игры как единственный или главный предмет разрабатывавшейся ими новой отрасли науки. На развитие теории вероятностей оказали влияние более серьезные потребности науки и запросы практики, и как мы уже говорили, в первую очередь, страховое дело, начатое в некоторых странах еще в XVI в. В XVI—XVII вв. учреждение страховых обществ и страхование судов от пожара распространилось во многих европейских странах. Азартные игры были для ученых только удобной моделью для решения задач и анализа понятий теории вероятности.
В развитии теории вероятностей велика и заслуга Пьера Симона Лапласа — ведущего математика восемнадцатого века
В его главном труде «Аналитическая теория вероятностей» рассмотрены азартные игры, геометрические вероятности, теорема Бернулли и ее связь с интегралом нормального распределения, теория наименьших квадратов, изобретенная Лежандром.
С работами Лапласа связано немало анекдотов. Хорошо известен предполагаемый ответ Лапласа Наполеону, который попытался упрекнуть его, заявив, что в его книге нет упоминаний о боге: «Государь, я не нуждался в этой гипотезе». А Натаниел Воудич из Бостона, который перевел четыре тома труда Лапласа на английский язык, как-то сказал: «Всегда, когда я встречал у Лапласа заявление «Итак, легко видеть...», я был уверен, что мне потребуются часы напряженной работы, пока я заполню пробел, догадаюсь и покажу, как это легко видеть».
В середине XIX в. преподаватель Высшей реальной школы в городе Брюнне (ныне — город Брно в Чехии) Грегор Иоганн Мендель проводил свои ставшие впоследствии знаменитыми опыты с горохом, в результате которых были открыты законы наследственности. Мендель скрестил два сорта гороха с желтыми и зелеными семенами, после чего растения дали только желтые семена (первое поколение гибридов). После самоопыления растений, выращенных из этих семян (второе поколение гибридов), появился горох и с желтыми, и с зелеными семенами. Мендель подсчитал, что отношение числа растений с желтыми семенами к числу растений с зелеными семенами равно  .
.
Впоследствии немецкий зоолог Август Вейсман и американский биолог Томас Хант Морган объяснили результаты опытов Менделя.
Предположим, что два элементарных носителя наследственности — доминантный ген  и рецессивный ген
и рецессивный ген 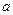 — отвечают в организме за некий признак. При этом данный признак задается парой генов
— отвечают в организме за некий признак. При этом данный признак задается парой генов 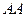 ,
, 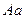 ,
,  , или
, или  и о соби с генами
и о соби с генами 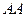 ,
, 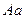 ,
,  имеют доминантный признак, а особи с генами
имеют доминантный признак, а особи с генами  — рецессивный. При скрещивании гороха
— рецессивный. При скрещивании гороха 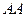 с горохом
с горохом  гибрид получает от каждого родителя по 1 гену, поэтому все особи первого поколения имеют пару генов
гибрид получает от каждого родителя по 1 гену, поэтому все особи первого поколения имеют пару генов 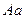 или
или  и у них обнаруживается доминантный признак: например, семена желтого цвета. От родителей с парами генов
и у них обнаруживается доминантный признак: например, семена желтого цвета. От родителей с парами генов 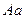 или
или  можно получить особь
можно получить особь 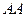 ,
, 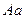 ,
,  или
или  . Все эти сочетания одинаково возможны, значит, особь
. Все эти сочетания одинаково возможны, значит, особь  с рецессивным признаком появляется с вероятностью
с рецессивным признаком появляется с вероятностью  , а особь
, а особь 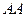 ,
, 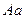 или
или  с доминантным признаком — с вероятностью
с доминантным признаком — с вероятностью 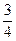 . Если во втором поколении было
. Если во втором поколении было  особей, где
особей, где 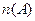 — число особей с доминантным признаком и
— число особей с доминантным признаком и 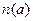 — число особей с рецессивным признаком, то при больших
— число особей с рецессивным признаком, то при больших 

а отношение  должно быть близким к 3. Это и установил Грегор Иоганн Мендель.
должно быть близким к 3. Это и установил Грегор Иоганн Мендель.
Механизм наследования так же случаен, как и исход бросания монеты или игральной кости. Поэтому можно сказать, что природа иногда «играет в кости».
Глава 1.7. Аксиомы теории вероятностей
Пусть проводится  испытаний. В результате каждого из них может произойти или не произойти случайное событие
испытаний. В результате каждого из них может произойти или не произойти случайное событие  : например, выпадет шестерка при бросании игральной кости, выпадут два орла при бросании двух монет и т. п. Обозначим
: например, выпадет шестерка при бросании игральной кости, выпадут два орла при бросании двух монет и т. п. Обозначим 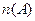 число испытаний, в которых произошло событие
число испытаний, в которых произошло событие  . Если при большом числе испытаний
. Если при большом числе испытаний  частота
частота  колеблется около некоторого числа
колеблется около некоторого числа 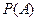 , то говорят: имеет место статистическая устойчивость частот, а число
, то говорят: имеет место статистическая устойчивость частот, а число 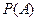 называют вероятностью события
называют вероятностью события  . Такая вероятность должна обладать свойствами, которые российский математик Андрей Николаевич Колмогоров сформулировал в виде трех аксиом.
. Такая вероятность должна обладать свойствами, которые российский математик Андрей Николаевич Колмогоров сформулировал в виде трех аксиом.
· Аксиома неотрицательности. Любая вероятность 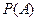 есть неотрицательное число:
есть неотрицательное число:
 .
.
· Аксиома нормированности. Вероятность достоверного события 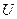 равна 1:
равна 1:
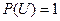 .
.
· Аксиома аддитивности. Вероятность суммы двух несовместных событий А и В равна сумме их вероятностей:
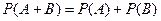 .
.
Колмогоров показал, что теорию вероятностей можно развивать на основе аксиом подобно обычной математической теории, как это делается, например, в геометрии.
Чтобы в этом убедиться, введем основные понятия, относящиеся к событиям.
Произведением 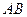 событий
событий  и
и 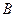 называют событие, которое происходит тогда и только тогда, когда имеют место оба события
называют событие, которое происходит тогда и только тогда, когда имеют место оба события  и
и 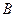 .
.
Например, событие  = [вынута карта червонной масти], событие
= [вынута карта червонной масти], событие 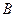 = [вынут туз], тогда произведением событий
= [вынут туз], тогда произведением событий  и
и 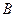 будет событие
будет событие  = [вынут червонный туз].
= [вынут червонный туз].
Суммой  событий
событий  и
и 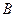 называют событие, которое происходит тогда и только тогда, когда имеют место либо событие
называют событие, которое происходит тогда и только тогда, когда имеют место либо событие  , либо событие
, либо событие 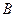 , либо оба вместе.
, либо оба вместе.
События  и
и 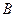 называют несовместными, если они одновременно не могут наступить.
называют несовместными, если они одновременно не могут наступить.
Событие 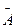 называют противоположным событию
называют противоположным событию  ,
,  если оно происходит всегда, когда не происходит событие
если оно происходит всегда, когда не происходит событие  .
.
Легко видеть, что события 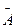 и
и  несовместны и по аксиоме аддитивности получим:
несовместны и по аксиоме аддитивности получим:
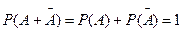 . (1.14)
. (1.14)
В более сложных случаях нельзя представить случайное событие  в виде конечного множества шансов из конечного числа равновероятных исходов.
в виде конечного множества шансов из конечного числа равновероятных исходов.
Например, рождение мальчика и девочки — не равновероятные случайные события. Известно, что на мальчиков приходится примерно 51 % от общего количества родившихся детей. В этом случае за вероятность события  = [рождение мальчика] принимается число
= [рождение мальчика] принимается число 
В дальнейшем рассмотрим несколько практических задач, а потому введем их нумерацию.
Задача 1. В коробке находится 10 шаров: 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.
Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.
Тогда в соответствии с формулой 1.12 получаем:
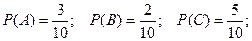
Отметим, что вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий.
Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.
Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:
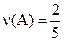 .
.
Как видно, эта величина не совпадает с найденной вероятностью.
При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события.
Вообще говоря, классическое определение вероятности – довольно относительное.
Это обусловлено тем, что на практике сложно представить результат опыта в виде совокупности элементарных событий, доказать, что события равновероятные.
К примеру, при произведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т. д.
Задача 2. В ящике имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно прочесть слово «спорт».
Рассуждаем на основе классического определения вероятностей. Пусть событие 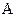 – полученное слово «спорт» из кубиков, тогда
– полученное слово «спорт» из кубиков, тогда  , где
, где  – число благоприятствующих исходов (в нашем случае он будет один),
– число благоприятствующих исходов (в нашем случае он будет один), 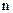 – общее число исходов (в нашем случае оно будет равно числу перестановок из пяти букв, т. е.
– общее число исходов (в нашем случае оно будет равно числу перестановок из пяти букв, т. е.  ). Тогда искомая вероятность
). Тогда искомая вероятность  .
.
Благодаря системе аксиом теория вероятностей окончательно оформилась в качестве полноправной математической науки. Она использует результаты из других разделов математики и, в свою очередь, оказывает на них значительное влияние.
В частности, благодаря и открытиям А.Н. Колмогорова в этой области, теорию вероятностей называют русской наукой. Познакомимся с жизнью этого великого ученого более подробно.

Рисунок 1.2. А.Н. Колмогоров
Колмогоров Андрей Николаевич родился 12(25) апреля 1903 г. в Тамбове. Мать Колмогорова умерла рано и его усыновила сестра матери, с которой они жили в родовом имении родителей матери в Ярославской губернии. В 1910 году, после переезда в Москву, поступил в частную гимназию. Здесь совместно обучались мальчики и девочки по программе мужской гимназии – явление уникальное в то время. Колмогоров имел по математике отличные успехи, и это позволило будущему ученому заниматься по этому предмету на класс старше. Однако на время интерес к другим наукам взял верх, и первый научный доклад, который 17-летний Колмогоров сделал в МГУ, был посвящен вовсе не математике, а новгородским землевладениям. И уже здесь при анализе писцовых книг XV–XVI вв. им были использованы элементы математической теории вероятностей.
Разработанные Колмогоровым аксиомы теории вероятностей послужили новым этапом в развитии этой науки.
Следует отметить, что наш институт ежегодно проводит математическую олимпиаду им. А. Н. Колмогорова среди школьников города Курска, победители и призеры которой становятся нашими студентами. Так наш институт чтит память о величайшем математике прошлого века.
Глава 1.8. Основные теоремы теории вероятностей
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 684; Нарушение авторских прав?; Мы поможем в написании вашей работы!