Рассмотрим без доказательства ряд теорем теории вероятностей и выясним их применение к практическим ситуациям

Теорема (сложения вероятностей).

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

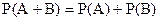. (1.15)

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

.(1.16)

Следствие. Сумма вероятностей противоположных событий равна единице.

. (1.17)

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.

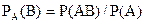. (1.18)

Например, в барабане 10 шаров, из которых 5 белых и 5 красных. Проводится опыт по двукратному извлечению шара. После первого извлечения шара из барабана шар в барабан не возвращается. Определить вероятность извлечения красного шара во втором опыте.

Если обозначить событие 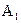– извлечение красного шара в первом опыте, то вероятность этого события равна .

Если обозначить событие – извлечение красного шара во втором опыте, то вероятность этого события будет носить условный характер, т.е. зависеть от того, что произошло в первом опыте. А значит, – в первом опыте извлечен был не красный шар, и – в первом опыте извлечен красный шар.

Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.

. (1.19)

Эту же теорему можно записать и в таком виде:

В связи с этим рассмотрим задачу. В читальном зале института 6 задачников по теории вероятностей, из которых три – в переплете. Библиотекарь наудачу взял два задачника. Найти вероятность того, что оба этих задачника окажутся в переплете.

Для решения снова введем обозначения событий. Пусть событие А – первый взятый задачник имеет переплет; событие В – второй взятый задачник имеет переплет. Вероятность того, первый взятый задачник имеет переплет равна: .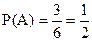

Вероятность того, что второй задачник имеет переплет, при условии, что первый взятый задачник был в переплете, т. е. условная вероятность события В равна 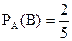. Искомая вероятность того, что оба задачника имеют переплет будет найдена по теореме умножения вероятностей событий, т. е. по равенству 1.19

.

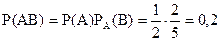Эта теорема остается справедливой для случая нескольких зависимых событий. Например, для совместного наступления трех зависимых событий эта теорема будет иметь вид:

. (1.19.1)

Если события независимые, то 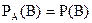, и теорема умножения вероятностей принимает вид:

. (1.20)

Например, пусть двое игроков бросают две игральные кости. Обозначим события:

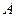= [на 1 -й кости выпадет шестерка],

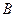= [на 2-й кости выпадет шестерка],

тогда

= [выпадут две шестерки].

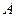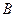Поскольку события и независимы, то

Эта теорема остается справедливой для случая нескольких независимых событий.

Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.

Если в результате испытания может появиться 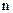событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна

. (1.21)

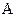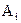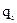Здесь событие обозначает наступление хотя бы одного из событий , а – вероятность противоположных событий

, т.е. .

Задача 3. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится герб.

Рассуждаем таким образом. В нашем случае элементарными событиями возможны следующие четыре события:

событие 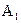– появление герба при двух бросках;

событие – появление герба при первом бросании;

событие 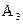– появление герба при втором бросании;

событие 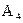– герб не появился ни разу. Благоприятствовать событию 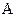(появление герба хотя бы один раз) будут события 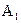, , 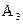. Следовательно, .

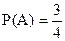Задача 4. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие 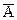, промах второго – событие .

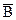Рассуждаем так, по условию задачи 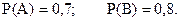Тогда в силу равенства 1.17 получаем, что и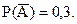

По теореме произведения событий вероятность того, что первый стрелок попадет в мишень, а второй – нет равна

.

Аналогично, вероятность того, что второй стрелок попадет в цель, а первый – нет равна

.

Тогда вероятность попадания в цель только одним стрелком равна

.

Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:

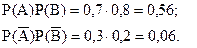
Тогда вероятность того, что в цель попадет только один стрелок равна:

Задача 5. Вероятность того, что взятая наугад деталь из некоторой партии деталей, будет бракованной равна 0,2. Найти вероятность того, что из трех взятых деталей 2 окажется небракованными.

Обозначим бракованную деталь – событие А, небракованную – событие .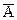

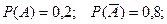
Если среди трех деталей оказывается только одна бракованная, то это возможно в одном из трех случаев: бракованная деталь будет первой, второй или третьей.

.

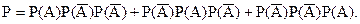
Глава 1.9. Формула полной вероятности

Дата добавления: 2015-06-04