Лекція 8

Стаціонарна теорія збурень (невироджений випадок)

Розв’язування рівняння Шредінґера для знаходження енергетичного спектра квантової системи та відповідних власних функцій оператора Ґамільтона 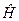(власних станів системи) може бути проведене точно лише у деяких спеціаль­них випадках. А саме, у випадку руху частинки в прямокутній потенціальній ямі, а також для гармонічного осцилятора, при проходженні частинки через потенціальний бар’єр та у випадку атома водню – про що вже йшлося вище, у Лекції 5. У біль­шості задач квантової механіки точного розв’язку отримати не можна. У зв’яз­ку з цим особливого значення набувають методи побудови наближених розв’яз­ків. У багатьох випадках є можливість наближено звести вихідну задачу з Ґамільтоніаном 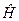до простішої задачі з Ґамільтоніаном 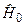, який дозволяє отри­мати точний розв’язок. Якщо ще при цьому Ґамільтоніани 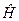та 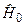„не силь­но відрізняються”, тобто якщо відповідні власні значення цих Ґамільтоніа­нів є достатньо близькими, то квантову систему з Ґамільтоніаном 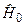розгляда­ють як опорну і вважають її нульовим наближенням до вихідної системи. Зруч­но ввес­ти у розгляд т. з. оператор „відхилення оператора 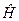” від опе­ра­тора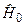

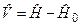. (8.1)

Саме цей оператор вносить збурення в Ґамільтоніан 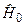опорної системи. Через це він ще має назву оператора збурення. Ґамільтоніан 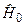ще вважають Ґаміль­тоніаном незбуреної задачі. Якщо оператори 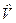та 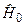не залежать від часу t, то наближений метод розв’язання задачі на власні значення та власні функції Ґамільтоніана 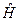, тобто вихідної задачі, має назву стаціонарної теорії збурень.

Представимо Ґамільтоніан 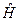у вигляді суми

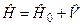, (8.2)

а рівняння

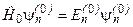(8.3)

вважатимемо розв’язаним, тобто власні значення 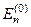та власні функції 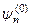нам відо­мі. Згадаймо, що нам необхідно знайти власне значення E_f та власну функ­цію ψ_f вихідного Ґамільтоніана 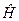, тобто необхідно розв’язати таке стаціонарне рівняння Шредінґера:

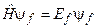. (8.4)

З усіх можливих випадків виділимо стаціонарну теорію збурень для задач з дискретним спектром енер­гії. Введемо для зручності параметр „вмикання” взаємодії ε:

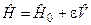, (8.5)

причому 0 ≤ ε ≤ 1. При ε=0 маємо незбурену задачу, а при ε=1 маємо вихідну за­дачу. Зважаючи на наявність параметра ε, запишемо рівняння, розв’язки якого нам треба знайти, у вигляді

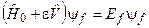. (8.6)

Розв’язки E_f та ψ_f формально будемо шукати у вигляді рядів по степенях пара­метра ε:

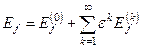, (8.7)

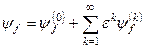. (8.8)

При значенні параметра ε=1 величини 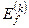та 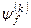, k =1, 2,… будемо називати по­правками до енергії 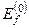і, відповідно, до хвильової функції 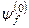. Так, величи­ни 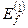та 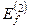називають першою та, відповідно, другою поправками до енергії 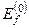незбу­реної задачі, а величини 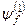та 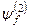– першою і, відповідно, другою по­прав­ками до хвильової функції 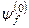незбуреної задачі. Після цього наша вихідна зада­ча звелася до знаходження відповідних поправок, а саме до визначення пов­но­го числа поправок 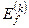та 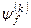, k =1, 2,… s, де s – число поправок, необхідних для досягнення потрібної точності обчислень.

Щоб знайти поправки 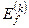та 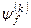, k =1, 2,… s, підставимо ряди (8.7) та (8.8) у рів­няння (8.6) і прирівняємо коефіцієнти при однакових степенях параметра ε. В результаті отримується наступна (нескінченна) послідовність рів­нянь:

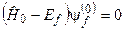, (8.9)

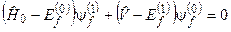, (8.10)

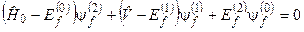, (8.11)

і т.д.

Перше рівняння з цієї послідовності є незбуреним, власні значення 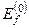та власні функції 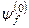вважаються відомими.

Задача 1. Знайти першу поправку 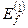до енергії 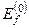незбуреної задачі.

Розв’язування. Розглянемо рівняння (8.9) та (8.10). Розкладемо функцію 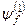в ряд по системі власних функцій оператора :

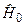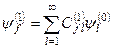. (8.12)

Тут через 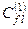позначено коефіцієнти розкладу. Підставимо (8.12) у (8.10) і отри­маємо

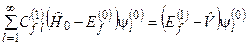. (8.13)

Обидві частини цього рівняння помножимо „зліва” на 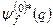і проінтегру­ємо по q обидві частини отриманого співвідношення:

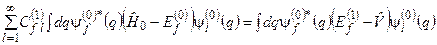. (8.14)

Врахуємо, що 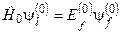і використаємо умову ортонормованості

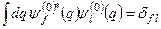. (8.15)

Отримаємо, що

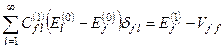, (8.16)

де вираз

(8.17)

у квантовій механіці має назву матричного елемента оператора .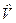

Зауваження. Величини V_lm (де індекси l та m незалежно пробігають всі зна­чен­ня 1, 2,…, і, нумеруючи власні функції із замкнутої системи власних функ­цій самоспряженого оператора) утворюють матрицю оператора 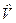. Матриця V_lm повніс­­тю задає оператор 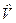. Отже, для знаходження оператора 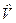достат­ньо обчислити його матричні елементи V_lm на хвильових функціях, що утво­рюють повну систему. Для зручності введемо діраківське позначення мат­ричних елементів оператора:

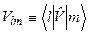(8.18)

Повернемося, однак, до співвідношення (8.16). Видно, що ліва частина цього рівнян­ня завжди рівна нулю. Адже, символ Кронекера δ _fl відмінний від нуля тільки при f = l, але в цьому випадку перетворюється в нуль множник 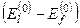). Остаточний резуль­тат приймає такий вигляд

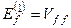. (8.19)

Висновок. Перша поправка до енергії рівна діагональному матричному еле­мен­ту оператора збурення, розрахованого на хвильових функціях незбуреної задачі:

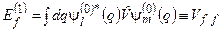. (8.20)

У першому наближенні по енергії (при ε=1) знаходимо

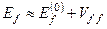. (8.21)

Задача 2. Знайти першу поправку 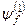до хвильової функції 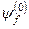незбуреної задачі.

Розв’язування. Розклад функції 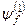по системі власних функцій оператора 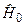запишемо у вигляді (див. також задачу 1)

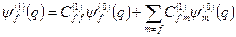. (8.22)

Твердження. З умови нормування хвильової функції 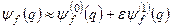випливає, що коефіцієнт

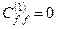. (8.23)

Приймемо це твердження без доведення (детальний виклад можна знайти в [1], стор. 390). Щоб знайти функцію

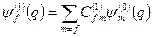, (8.24)

слід знайти коефіцієнти розкладу 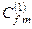з m ≠ f. Знову помножимо обидві частини рів­няння (8.10) „зліва” на 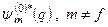, і від обох частин візьмемо інтеграл по q. Отримаємо

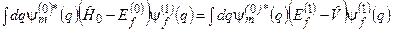, (8.25)

або

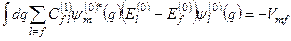. (8.26)

При отриманні останньої рівності було враховано, що 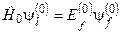і 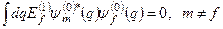. Рівняння (8.26) може набути ще такого вигляду

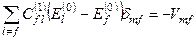(8.27)

або

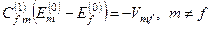. (8.28)

Остаточно,

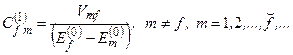, (8.29)

де символ 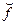означає, що m ≠ f.

Висновок. Перша поправка 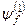до хвильової функції 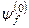незбуреної задачі має вигляд

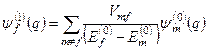. (8.30)

Отже, у першому наближенні при ε=1 маємо (поряд з виразом (8.21) для енер­гії):

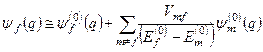, (8.31)

де V_ml знаходиться з рівності (8.17) при (m, l) = 1, 2,...

Задача 3. Знайти друге наближення для енергії, тобто знайти

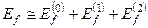. (8.32)

Розв’язування. Розглянемо рівняння (8.11). Розкладемо функцію 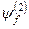в ряд по системі власних функцій оператора :

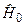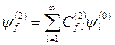. (8.33)

Підставимо цей розклад у рівняння (8.11) і одержимо, що

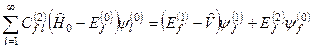. (8.34)

За аналогією з попередніми завданнями, помножимо ліву і праву частини цього рів­нян­ня „зліва” на 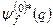і проінтегруємо по q отримане співвідношення:

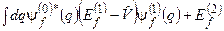. (8.35)

Але

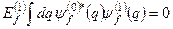, (8.36)

оскільки ми знаємо, що 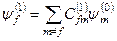, і має місце умова нормування 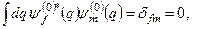при 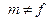. Тоді

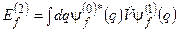(8.37)

або

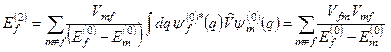. (8.38)

Висновок. Таким чином, при ε=1 у другому наближенні

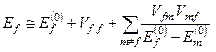. (8.39)

З ермітовості оператора збурення слідує V_mf = V_fm^*, отже V_mf V_fm = | V_mf |². Для основно­го стану, тобто коли f =0, друга поправка

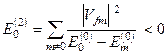, (8.40)

адже 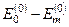<0 (за означенням!). Цей факт має фізичний зміст: сили Ван-дер-Ваальса мають характер притягання.

Умови застосовності розглянутої теорії збурень зводяться до вимоги „ма­лості” поправок до хвильової функції (вектора стану). Це, в свою чергу, озна­чає, що повинна виконуватися умова 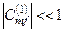. Звідси знайдемо у явному вигля­ді умову застосовності теорії збурень:

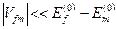. (8.41)

Дата добавления: 2015-06-04