Результаты поэтапного выполнения алгоритма обратногораспространения ошибки

К лабораторным работам

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по курсу ²Электроника²

Редактор: к.т.н., доцент Удальцов А.Н..

Корректор:

Подписано в печать

формат бумаги А5, отпечатано на ризографе, шрифт №10,

изд. л ____, заказ №___, тираж -600.

Типография СибГУТИ, 6300102, Новосибирск, ул. Кирова, 86

Этап	Прямое распространение входного сигнала	Обратное распространение ошибки	Изменение весов
A1(1),A1(2)	Logsig{WxP+Вх)= [0,321, 0,368]	Не выполняется	Не выполняется
А2	purelin (WlP +В1)= 0,446	То же	То же
e	t-А2=1,261	»	»
N1(1), N1(2)	Не выполняется	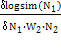= [-0.049,0.100]	»
N2	То же	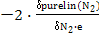= -2.522	»
W1(1),W1(2)	»	Не выполняется	W1=W1-lr×N1×P=[-0.265-0.420]
B1(1),B1(2)	»	То же	B1=B1-lr×N1 =[-0.475-0.140]
B2	»	»	B2=B2-lr×N2 =0.732
W2(1),W2(2)	»	»	W2=W2-lr×N2×N1 = [-0.171,0.140]

Lr – коэффициент обучаемости.

Пусть входной сигнал Р =1,0, а желаемый выход t = 1 + sm(p * к/4) = 1,707.

Результаты выполнения этапов алгоритма представлены в табл. П2.

Контрольные вопросы

1. Каким алгоритмом обучают многослойные НС?

2. Из каких основных этапов состоит алгоритм обратного
распространения ошибки?

3. Почему алгоритм обратного распространения ошибки относится к классу алгоритмов градиентного спуска?

4. Как влияет функция принадлежности на правило изменения весов в обратном алгоритме распространения ошибки?

Лабораторная работа № 6.

Изучение радиальных базисных, вероятностных нейронных сетей, сетей регрессии

Цель работы: изучить модель вычислений радиального базисного нейрона, структуру и функции сетей регрессии, вероятностных нейронных сетей.

Функция newrb создает радиальную базисную сеть и имеет следующий синтаксис:

net = newrb (Р, Т, goal, spread).

Радиальные базисные сети используют для аппроксимации функций. Функция newrb конструирует скрытый (первый) слой из радиальных базисных нейронов и использует значение средней квадратичной ошибки (goal).Функция newrb(P,Т, goal, spread) имеет следующие аргументы: Р – матрица Q входных векторов размерности R на Q; Т – матрица Q векторов целевых классов S на Q\ goal – средняя квадратичная ошибка, по умолчанию 0,0; spread – разброс радиальной базисной функции, по умолчанию 1,0. Функция создает и возвращает в качестве объекта радиальную базисную сеть. Большое значение разброса приводит к большей гладкости аппроксимации. Слишком большой разброс требует много
нейронов, для того чтобы подстроиться под быстро изменяюшуюся функцию, слишком малый – для достижения гладкости аппроксимации. Подобрать значение разброса можно
с помощью многократных вызовов функции newrb. Создадим в среде Matlab радиальную базисную сеть:

net = newrbe(P, Т, spread).

Функция newrbe проектирует радиальную базисную сеть с нулевой ошибкой для заданных векторов. Функция newrbe(P, Т,spread) имеет три параметра: Р – матрица £) входных векторов размерности R на Q, Т – матрица £) целевых векторов --описателей класса размерности S на Q, spread – разброс радиальной базисной функции, по умолчанию 1,0. Функция создает радиальную базисную сеть. Нейронная сеть регрессии – это вид радиальной базисной сети, которая часто используется для аппроксимации функций и быстро строит сеть для аппроксимации: net = newgrnn(P, Т,spread).

Функция

newgrnn(P, Т, spread)

имеет следующие входы: Р – матрица Q входных векторов размерности /?на Q, Т – матрица Q целевых векторов классов размерности S на Q, spread – разброс радиальных базисных функций, по умолчанию 1,0. Функция возвращает НС регрессии. Чем больше разброс, тем более гладкой будет функция аппроксимации. Для того чтобы настроить функцию аппроксимации на исходные данные, используют разброс меньший, чем типичное расстояние между входными векторами.

Функция newgrnn создает двухслойную сеть. Первый слой содержит радиальные базисные нейроны, вычисляющие расстояние между входами и весами с помощью netprod. Второй слой имеет нейроны с функцией активации purelin. Только у первого слоя существует bias.

Вероятностную нейронную сеть проектируют с помощью функции

net = newpnn(P, Т, spread).

Вероятностная НС – это вид радиальной базисной сети, как и НС регрессии, но данные сети используются для решения задачи классификации, а не аппроксимации. Функция net = newpnn(P, T9 spread) имеет такие же параметры, как
и вышеописанная функция newgrnn. Если разброс близок к нулю, вероятностная НС действует как классификатор на основе принципа выбора «ближайшего соседа», в противном случае сеть принимает в расчет несколько близких векторов.

Пример П22. Создание и обучение НС регрессии.

Рассмотрим проектирование НС регрессии. Определим:

\\ входы НС регрессии
Р = [1 2 3];
\ \ выходы НС регрессии.
Т = [3,0 5,1 4,8];

Воспользуемся функцией newgrnn для создания НС регрессии. Зададим разброс радиальных базисных функций (переменная spread) меньше, чем 1, для того чтобы получить хорошую аппроксимацию данных и более гладкую функцию.

\\ установка разброса радиальных базисных функций
Spread = 0,8;

\\ создание НС регрессии
net = newgrnn (Р, Т, spread);

\\ имитация работы НС регрессии
А = sim (net, Р);

\\ изображение аппроксимируемой функции
plot(P, Т, '. ', 'markersize', 30);
\ \ установка режима добавления графиков на координатные оси
hold on,

\\ изображение работы необученной НС регрессии
plot(P, А, '. ','markersize', 30, 'color', [1 0 0]);

cla reset'; \\ очистка координатных осей

р = 4,5; \\установка нового входа НС регрессии

а = sim (net, р); \\ получение отклика НС регрессии

\\ изображение аппроксимируемой функции
plot(P, Т, '. ', 'markersize', 30);

axis ([0 9 – 1 4]); \\ установка диапазонов осей X и У
hold on; \\ включение режима добавления графиков
\\ изображение отклика НС регрессии на вход р
plot(p, а, '.', 'markersize', 30, 'color', [1 0 0])/
title ('Новый входной вектор');
\ \ написать заголовок графика

xlabel ('P и p'); \\ пометить ось X

у label('T и a 1); \\ пометить ось X

cla reset; \\ очистить координатную сетку

р2 - 0: 2: 9; \\ определить последовательность входов Р2

Сымитируем отклик сети для различных значений, чтобы увидеть результат аппроксимации (рис. П26).

\ \ получить отклик НС регрессии на последовательность входов Р2
&2 = sim (net, Р2);
\ \ изобразить отклик НС регрессии
plot(P2f К2, 'linewidth', 4, 'color9, [1 0 0]);
hold on; \\ включить режим добавления графиков
\ \ изобразить аппроксимируемую функцию
plot(Р, Т, '. ', 'markersize', 30);
axis ([0 9 – 1 4]); \\ установить диапазон осей
title('Аппроксимируемая функция'); \\ озаглавить график
xlabel('Р и Р2'); \\ пометить ось X
ylabel('T и А2 '); \\ пометить ось Y

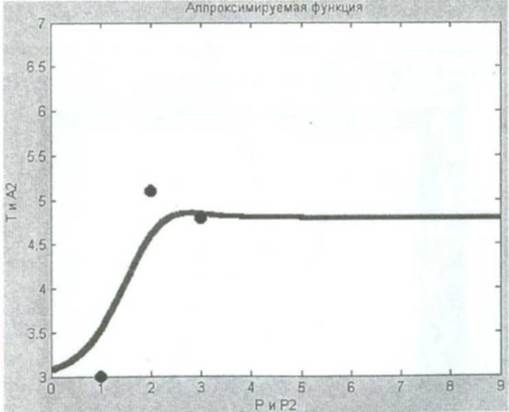
Рис. П26. Аппроксимация точек с помощью нейронной сети регрессии

Пример П23. Использование РБНС для аппроксимации функций.

Рассмотрим аппроксимацию функций на основе радиальной базисной сети.

Пусть J

\\ определение диапазона значений радиальной базисной функции
р = -4: 2: 4; 1

\ \ вычисление радиальной базисной функции на диапазоне р
а = radbas (р);

plot (р, а); \\ изображение РБФ

title ('Радиальная базисная функция ');

\\ озаглавить график

xlabel ('Вход р'); \\ пометить ось X
уlabel ('Выход а '); \\ пометить ось У

На рис. П27 изображена радиальная базисная функция. Функция newbe создаст необходимую сеть. Зададим аппроксимируемую функцию как набор точек:

\ \ определение последовательности аргументов аппроксимируемой функции Р
Р = -1: 1: 1;

\\ определение значений аппроксимируемой функции,
\\ соответствующих Р

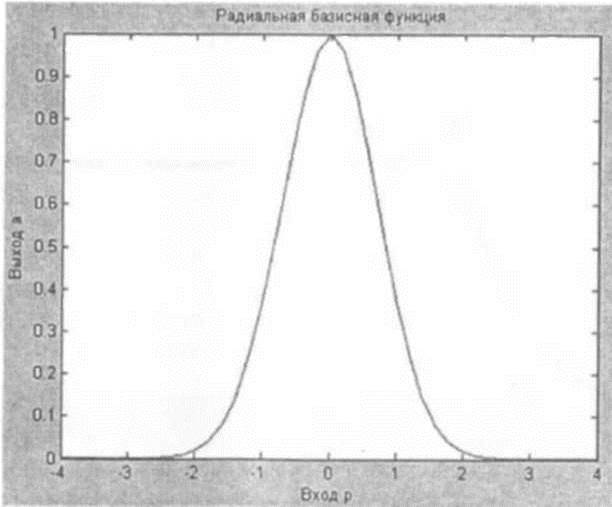
Рис. П27. Радиальная базисная функция

T = [-.6662 -.3766 -.1129.2111.6565.3301.3649.2006-.1913 -.3994 -.5022 -.4531 -.1133.0866.3333.4955.3488.2833 -.1112 -.6685 -.3255];

Изобразим график функции (рис. П28).

plot (Р, Т, ' * '); \\ изображение аппроксимируемой функции
title('Обучающая выборка '); \\ озаглавить график
xlabel('Входной вектор Р'); \\ пометить ось X
уlabel ('Вектор Т'); \\ пометить ось У

Далее необходимо найти функцию, которая хорошо описывает заданную 21 точку.

Функция newrb создает РБНС для аппроксимации:

е = 0,02; % целевой среднеквадратичной ошибки

sp = 1; % разброса РБФ

net = newrb(Р,Т,е,sp); создание РБФ

X = -1:.01: 1; \\ определение вектора входов

Сымитируем работу сети.

У = simfnet, X); \\ формирование отклика У
hold on; \\ включение режима добавления графика
plot(X, У); \\ изображение результатов аппроксимации
hold off; \\ отключение режима добавления графика

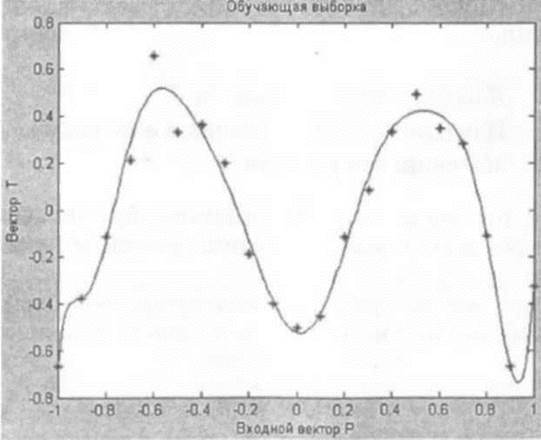
Рис. П28. Результат аппроксимации с помощью радиальной базисной нейронной сети

Пример П24. Использование вероятностной НС для классификации векторов.

Рассмотрим задачу классификации с набором входов Р и множеством классов, обозначенным Тс.

\\ определение входов
Р = [1 2 3 4 5 6 7];

Тс = [1 1 3 3 2 1 1]; \\ определение желаемых выходов
\\ конвертирование индексов в векторы, содержащие

1 в индексных позициях
Т = ind2vec (Тс);

net = newpnn(P, Т); \\ создание вероятностной НС
Y = sim (net, Р); \\ имитация работы вероятностной НС
Yc = vec2ind(Y); \\ конвертирование номеров классов в векторы.

Контрольные вопросы

1. Какую функцию называют радиальной базисной функцией?

2. Из каких слоев состоит радиально-базисная НС?

3. Из каких слоев состоит НС регрессии?

4. Из каких слоев состоит вероятностная НС?

5. Какие виды НС предназначены для решения задачи аппроксимации функций, а какие – для классификации объектов?

Лабораторная работа № 7.

Изучение сетей Кохонена и алгоритма обучения без учителя

Цель работы: изучить алгоритм обучения без учителя на примере задачи кластеризации, алгоритм «победителя» Кохонена. Функция net возвращает соперничающий слой. Соперничающий слой используется для решения задачи классификации

net = newc(PR, S, KLR, CLR),где:

× PR – матрица минимальных и максимальных значений для R
входных элементов;

× S – количество нейронов;

× KLR – уровень обученности Кохонена, по умолчанию 0,01;

× CLR – рекомендуемый уровень обученности, по умолчанию 0,001.

Соперничающий слой представляет собой слой с функцией вычисления расстояний negdist, сетевой функцией суммирования rttsum и функцией активации compet. Слой имеет веса на входах и bias.

Функция newsom создает самоорганизующуюся сеть – карту (SOM), которая решает задачу классификации:

net = newsom(PR, [dl, d2,...],
7TO; DFCN, OLR, OSTEPS, TLR, TND), где:

× PR – матрица минимальных и максимальных значений для R входных элементов;

× I – размер I-го слоя;

× TFCN – функция топологии;

× DFCN – функция расстояния;

× OLR – уровень обученности фазы упорядочения, по умолчанию 0,9;

× OSTEPS – шаги фазы упорядочения, по умолчанию 1000;

× TLR – уровень обученности фазы настройки, по умолчанию 0,02;

× TND – расстояние соседства фазы настройки, по умолчанию 1.

Пример П25. Создание и использование соперничающего слоя.

Рассмотрим пример использования соперничающего слоя. Зададим множество, состоящее из четырех двухэлементных векторов Р.

Р = [.2.5.1.8;.3.7.2. 6]; \\ определение входного
вектора

Соперничающий слой должен разделить входы на два класса:
net = newcilQl; 0 1], 2); \ \ создание соперничающегослоя

net = train (net, Р); \\ обучение соперничающего слоя на векторе Р

Результирующая сеть выдает выходной вектор, конвертируемый в номер класса:

Y = sim(net, Р)! W имитация работы слоя

Yc = vec2ind(Y) / W конвертирование выхода сети в номер кявсса
У состоит из векторов, содержащих только по однойединице.

Функция vec2ind показывает индексы единичных позиций.

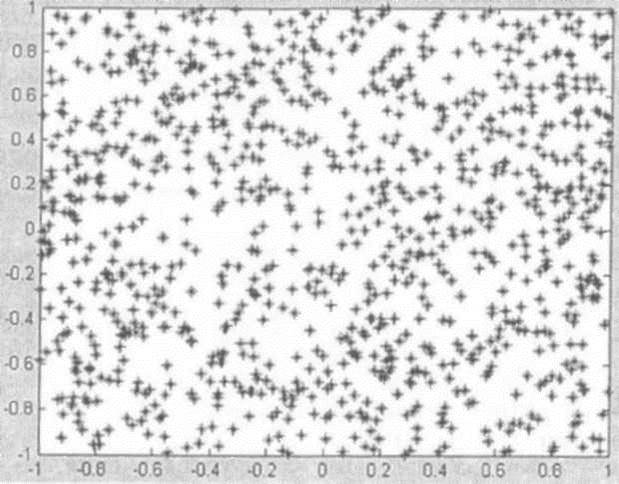
Рис. П29. Множество исходных векторов для кластеризации

Пример П26. Применение SOM для кластеризации векторов.

Рассмотрим работу SOM на примере задачи классификации 1000 двухэлементных векторов, расположенных в ограниченной прямоугольной области (рис. П29).

\\ определение множества векторов для кластеризации
Р = rands(2, 1000);

plot(P(1,:), Р(2,:), '*g'); \\ изображение множества векторов

Создадим SOM:

net = newsom([0 1; 0 1],[5 6]); \\ создание SOM размерностью 5 х 6

Используем сеть размерностью 5x6, чтобы классифицировать вышеопределенные векторы. Создадим сеть с 30 центрами, к которым сеть будет относить каждый вектор на основе ближайшего соседства.

plotsom (net.iw{1,1}, net.layers{1}.distances);
\\ визуализация SOM

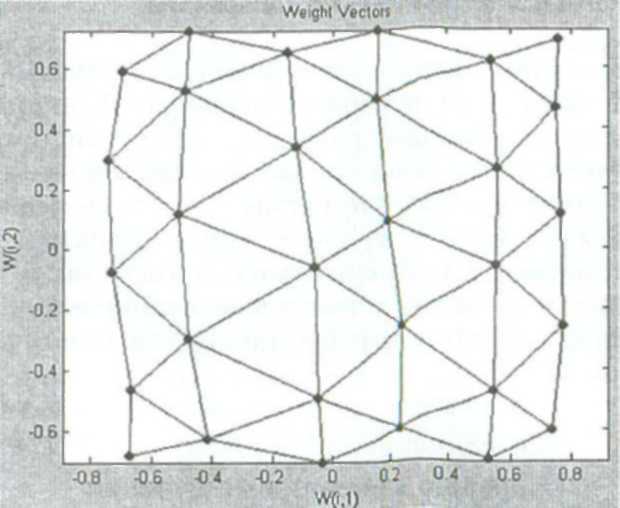
Рис. ПЗО. Самоорганизующаяся карта кластеризации

Сначала центр прямоугольника совпадает с центрами классов. Обучим сеть на 100 эпохах и изобразим результат (рис. ПЗО):

net.trainParam.epochs = 100;
\\ установка количества эпох
net = train (net, Р); \\ обучение сети
plotsom (net.iw {1,1}, net.layers{1}.distances);
\\ визуализация SOM

p = [0,3; 0,5]; \\ определение нового вектора

a = 0; \\ начальная установка переменной а

а = sim (net, р); \\ получение отклика SOM вход р

Контрольные вопросы

1. В чем заключается задача кластеризации?

2. Какую структуру имеет НС Кохонена?

3. Каким алгоритмом обучается НС Кохонена?

П.З. Генетические алгоритмы

Учебный практикум по генетическим алгоритмам составлен как задание на разработку основных функций в среде Matlab, так как в распространяемых версиях системы расширение toolbox не содержит третью компоненту мягких вычислений – генетические алгоритмы. Полезным упражнением будет служить множество элементарных функций генетических алгоритмов. Практикум включает в себя также набор оптимизационных задач, в том числе классических, которые можно будет решать в разработанной среде генетических вычислений Matlab.

Лабораторная работа № 8.
Основные элементарные функции генетических вычислений.

Цель работы: изучить базовые операторы стандартного и мобильного генетических алгоритмов, эволюционных стратегий.

Для реализации в среде Matlab генетических вычислений необходимо разработать следующие элементарные функции.

Функция	Назначение
Chromobin(length, cod)	Задает хромосому в форме бинарной строки длины length, если cod = 0, используется двоичное кодирование, если cod = 1, используется код Грэя.
Chromoint (length)	Задает хромосому в форме последовательности целых чисел длины length.
Chromolist(length)	Задает хромосому в форме списка пар (номер гена, целое значение) длины length.
InitPopulation (rand, cht, S)	Создает исходную первичную популяцию объектов – хромосом, причем rand – это функция порождения случайной хромосомы, cht – тип хромосомы (Chromobin, Chromoint, Chromolist), по умолчанию Chromobin, S – количество хромосом в популяции.
Mutationbin (chromo)	Мутация в форме инверсии случайно выбранного гена хромосомы chromo.
Mutationint (chromo, max)	Мутация случайно выбранного гена дополнением до max значения.
Mutationlist(chromo, max)	Мутация случайно выбранного гена дополнением до max значения.
Recombinationbin(chromo1, chromo2)	Возвращает двух потомков, составленных из родительских фрагментов chromo1, chromo2, причем фрагменты получены в случайной точке разрезания, а хромосомы – это бинарные строки.

Функция	Назначение
Recombinationint (chromo1, chromo2)	Возвращает двух потомков, составленных из родительских фрагментов chromo1, chromo2, причем фрагменты получены в случайной точке разрезания, а хромосомы – это последовательности целых.
Recomhinationbinm (chromolist, parents, sons)	Возвращает потомков в количестве sons, составленных из родительских фрагментов, причем список chromolist содержит родителей в количестве parents. Фрагменты получены в случайных точках разрезания случайных родителей из chromolist, а хромосомы – это бинарные строки.
Recombinationintm (chromolist, parents, sons)	Возвращает потомков в количестве sons, составленных из родительских фрагментов, причем список chromolist содержит родителей в количестве parents. Фрагменты получены в случайных точках разрезания случайных родителей из chromolist, а хромосомы – это последовательности целых чисел.
Rang(Р, fitfunction)	Ранжирование хромосом популяции Р с помощью функции оптимальности fitfunction, причем функция оптимальности задается конкретно для каждой проблемной области.
Selection (Pparents)	Пропорциональный отбор хромосом из популяции Р. Возвращает под популяцию хромосом, участвующих в формировании следующего поколения.
Newgeneration (Fold, Pparents, elite)	Формирует новое поколение популяции из старой популяции потомков, выбранных для рекомбинации хромосом Pparents, причем, если параметр elite = 0, то элитное сохранение лучших не используется, если elite – целое число, то столько лучших хромосом текущего поколения переходит в следующее.
InitPopulationM (rand, S)	Создает исходную первичную популяцию объектов – хромосом, причем rand – функция порождения случайной хромосомы, S – количество хромосом в популяции, причем формируются не полностью определенные хромосомы типа Chromolist. Функция используется для мобильного генетического алгоритма.
Cut (cromo)	Разрезает хромосому типа Chromolist в случайном месте.
Splice (chromo1, chromo2)	Склеивает две хромосомы типа Chromolist, причем в результирующей хромосоме возможно дублирование генов, которые доминируют слева направо.
AccumulatePop (Р, q)	Функция разрезает и склеивает хромосомы популяции Pop, причем склеивание доминирует над разрезанием. Функция реализует стадию насыщения мобильного ГА. Параметр q – количество поколений в стадии насыщения.

Контрольные вопросы

1. Как выполняется оператор пропорционального отбора в стандартном ГА?

2. Как выполняется оператор скрещивания в стандартном ГА?

3. Как выполняется оператор мутации в стандартном ГА?

4. Каким образом кодируют хромосомы?

5. Что выполняют операторы Cut и Splice в мобильном ГА?

6. Какой ГА использует хромосомы переменной структуры: стандартный или мобильный?

Лабораторная работа № 9.
Интегральные функции генетических вычислений

Цель работы: изучить генетические алгоритмы – стандартный, мобильный, эволюционные стратегии.

Интегральные функции генетических вычислений реализуют стандартный ГА, включая «только мутацию», ГА со сложной рекомбинацией и мобильный ГА.

Функция standartga (cht, qpop, initpopfun, mutfun, recfun, fitfun, rangfun, selfun, newgen, terminationcond, fitgoalpmut, precom) реализует генетическую оптимизацию популяции хромосом типа cht размера qpop, которая инициализируется функцией инициализации initpopfun. Генетическая оптимизация использует оператор мутации типа mutfun с вероятностью pmut, оператор рекомбинации – с вероятностью precom. Ранжирование, селекция и формирование нового поколения осуществляются функциями rangfun, selfun, newgen соответственно на основе функции оптимальности fitfun. Завершение оп-
тимизации задается либо параметром terminationcond, как число поколений, либо параметром fitgoal, как целевым значением функции оптимальности. Если параметр pmut = 0, то мутация не используется; если precom = 0, то рекомбинация
не используется и стандартный ГА превращается в алгоритм «только мутация».

Функция mobilga (qpop, initpopfun, accumfun, cutfun, splicefun, fitfun, rangfun, selfun, newgen, terminationcond, fitgoal, pcut, psplice) реализует генетическую оптимизацию популяции хромосом размера qpop с помощью мобильного ГА, которая инициализируется функцией инициализации initpopfun. Стадия насыщения реализуется функцией accumfun. Генетическая оптимизация использует оператор разрезания cutfun с вероятностью pcut, оператор склеивания – с вероятностью psplice. Ранжирование, селекция и формирование нового поколения осуществляются функциями rangfun, selfun, newgen соответственно на основе функции оптимальности fitfun. Завершение оптимизации задается либо параметром terminationcond, как число поколений, либо параметром fitgoal, как целевым значением функции оптимальности.

Контрольные вопросы

1. Из каких этапов состоит стандартный ГА?

2. Что такое эволюционная стратегия?

3. Какие параметры ГА позволяют управлять его сходимостью?

4. Какими особенностями обладает мобильный ГА?

5. В чем заключается этап генерации популяции для стандартного и мобильного ГА?

Лабораторная работа № 10.
Прикладные оптимизационные задачи

Цель работы: изучить особенности применения генетических алгоритмов к оптимизационным задачам, получить опыт применения ГА к конкретной проблемной области.

Список оптимизационных задач, которые могут быть решены с помощью генетических вычислений, составим на основе классических оптимизационных задач и прикладных задач автоматизированного проектирования технических объектов.

Перечислим классические задачи оптимизации, приемлемые для демонстрации мощности генетических вычислений.

Задача о диете. Рассмотрим задачу составления наиболее экономного (дешевого) рациона питания, удовлетворяющего определенным медицинским требованиям. Известен перечень доступных продуктов из N наименований. Кроме того, рассматриваются такие характеристики продуктов, как витамины, минеральные вещества, жиры, белки, углеводы, калорииность. Для каждого продукта известна его медицинская характеристика, т. е. количественное содержание в одной единице указанных компонент. Приемлем рацион, удовлетворяющий медицинским нормам, оптимальным является самый дешевый из них.

Транспортная задача. Имеется m пунктов S₁, S₂, …, S_m производства однородного продукта (стали, цемента и т.д.), причем объем производства в пункте S_i равен a_i. Произведенный продукт используется в пунктах Q₁,Q₂,...., Q_n, и потребность в нем в пункте составляет b_j единиц. Требуется найти оптимальный путь из пунктов S_i в пункты Q_j чтобы удовлетворить потребности в продукте b_j не допуская затоваривания пунктов производства и минимизируя транспортные расходы.

Задача рационального использования посевных площадей. Имеется m земельных угодий S₁, S₂, …, S_m, предназначенных для засева той или иной сельскохозяйственной культурой. Эти площади отличаются положением и характером почвы. На каждом из угодий S_i могут быть размещены одна или несколько из n сельскохозяйственных культур Q₁, Q₂, …, Q_n. Пусть известна урожайность культуры Q_j на поле S_i, она равна а_ij ц/га. Будем обозначать площадь поля S_i в гектарах через a_i. Ограничения на приемлемое решение следующие: задан план производства b_j каждой сельскохозяйственной культуры Q_j. Известны закупочные цены C_j на каждый вид продукции. Найти оптимальный план засева посевных площадей с максимальной прибылью от продажи сельхозпродукции.

Задача межотраслевого баланса. Допустим, что в некоторый момент времени, в году T₀ по итоговым данным составлен балансовый отчет по народному хозяйству за фиксированный период по форме табл. ПЗ.

Величины А_ij указывают объем продукта с номером i, израсходованный отраслью j. Числа V_j равны общему объему продукции j -й отрасли, а С_i – объему продукции j -й отрасли, который был потреблен в непроизводственной сфере. Балансовый характер таблицы выражается уравнением

∑ _j А_ij = V_j – С_i

Будем считать технологию производства неизменной и линейной. Допустим, что все отрасли будут работать так, что отрасль с номером j произведет объем x _j валового выпуска своей продукции, т. е. отрасль j работает с интенсивностью х_j. Необходимо найти оптимальный вектор интенсивности X при описанных ограничениях. Другими словами, необходимо решить уравнение X – АХ = С. Это уравнение вместе с изложенной выше интерпретацией матрицы А и вектора X называется моделью Леонтьева.

Таблица П3

Дата добавления: 2015-06-04