Вычисление определенного интеграла

Основные свойства определенного интеграла

(1)

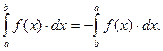
(2) 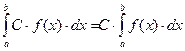, где С – const.

(3) .

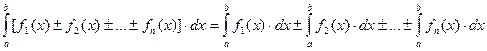(4)

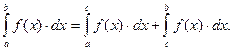
Свойство (4) справедливо при любом взаимном расположении точек a, b, c и при условии интегрируемости функции на каждом из этих интервалов.

Основной способ вычисления определенных интегралов основан на использовании связи между определенным и неопределенным интегралами от рассматриваемой функции. Следствием этой связи является формула Ньютона-Лейбница, которая имеет вид:

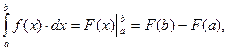
Где F(x) – любая первообразная для f(x) на промежутке [ a, b ]. Таким образом, значение определенного интеграла от данной функции f(x) на интервале [ a, b ] равно разности значений какой-либо первообразной этой функции на верхнем и нижнем пределах интегрирования.

Пример 23.

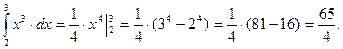
Пример 24.

.

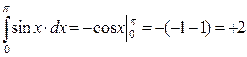Пример 25.

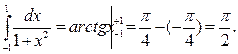
Поскольку формула Ньютона-Лейбница позволяет легко выразить определенный интеграл через значения первообразной для подынтегральной функции, то, очевидно, что при вычислении определенных интегралов могут быть использованы основные методы вычисления неопределенных интегралов: метод подстановки и метод интегрирования по частям.

В случае определенного интеграла формула (13) замены переменной переходит в

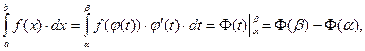
где а Ф(t) - первообразная для функции .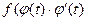

Отметим, что применение метода подстановки даже несколько упрощается, так как нет необходимости возвращаться к первоначальной переменной в выражении, полученном для первообразной. Достаточно вычислить разность ее значений на верхнем и нижнем пределе изменения новой переменной.

Пример 26.

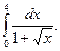
Произведем замену переменной. ,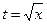

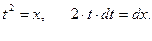
Пределы интегрирования х=0, t=0, x=4, t=2.

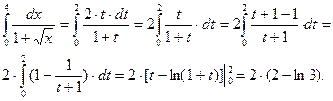
Пример 27.

.

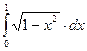Пределы интегрирования позволяют использовать для замены переменой тригонометрические функции.

x = sin t, d x = cos t∙dt; x = 0, t = 0; x = 1, t = π/2.

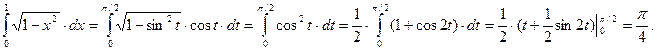
Формула интегрирования по частям применительно к вычислению определенного интеграла записывается как:

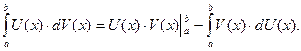
Пример 28.

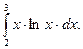
Применяем метод интегрирования по частям, полагая:

,

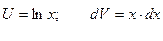Тогда: 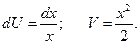Следовательно:

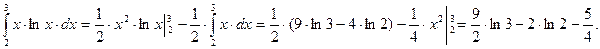
Дата добавления: 2015-06-04