Линейные однородные ДУ второго порядка

Рассмотрим линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка:

(1.13)

и установим некоторые свойства его решений.

Теорема 1.2. Если функци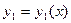и и 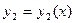являются частными решениями уравнения (1.13), то решением этого уравнения является также функция

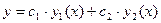, (1.14)

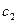где и - произвольные постоянные.

Подставим функцию и ее производные в левую часть ЛОДУ (1.13).

Получаем:

,

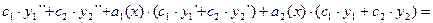
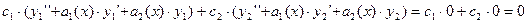так как функци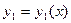и и 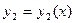- решения уравнения (1.13) и, значит, выражения в скобках тождественно равны нулю.

Таким образом, функция 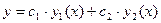также является решением уравнения (1.13).

Из теоремы 1.2, как следствие, вытекает, что если и - решения уравнения (1.13), то решениями его будут также функции и .

Функция (1.14) содержит две произвольные постоянные и является решением уравнения (1.13). Может ли она являться общим решением уравнения (1.13)?

Для ответа на вопрос введем понятие линейной зависимости и линейной независимости функций.

Функци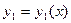и и 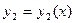называются линейно независимыми на интервале 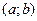, если равенство

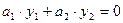, (1.15)

где 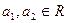, выполняется тогда и только тогда, когда .

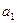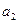Если хотя бы одно из чисел или отлично от нуля и выполняется равенство (1.15), то функции и называются линейно зависимыми на .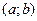

Очевидно, что функции и линейно зависимы тогда и только тогда, когда они пропорциональны, т. е. для всех 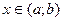выполняется равенство , или , .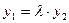

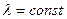Например:

функции и линейно зависимы: ;

функции и - линейно независимы: ;

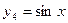функции и 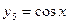являются линейно независимыми: равенство 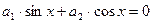выполняется для всех 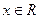лишь при (или ).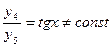

Средством изучения линейной зависимости системы функций является так называемый определитель Вронского или вронскиан (Ю. Вронский - польский математик).

Для двух дифференцируемых функци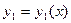й и 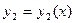вронскиан имеет вид

.

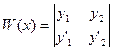Имеют место следующие теоремы.

Теорема 1.3. Если дифференцируемые функци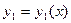и и 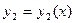линейно зависимы на 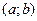, то определитель Вронского на этом интервале тождественно равен нулю.

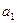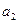Так как функции и линейно зависимы, то в равенстве (1.15) значение или отлично от нуля. Пусть 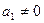, тогда ; поэтому для любого

.

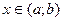
Теорема 1.4. Если функции и 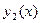- линейно независимые решения уравнения (1.13) на 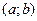, то определитель Вронского на этом интервале нигде не обращается в нуль.

Доказательство теоремы опустим.

Из теорем 1.3 и 1.4 следует, что вронскиан не равен нулю ни в одной точке интервала 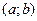тогда и только тогда, когда частные решения линейно независимы.

Совокупность любых двух линейно независимых на интервале 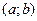частных решений и 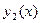ЛОДУ второго порядка определяет фундаментальную систему решений этого уравнения: любое произвольное решение может быть получено как комбинация

.

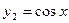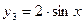Пример 1.4. Частные решения и , и : (их бесчисленное множество!) уравнения 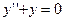образуют фундаментальную систему решений; решения же и - не образуют.

Теперь можно сказать, при каких условиях функция (1.14) будет общим решением уравнения (1.13).

Теорема 1.5 (структура общего решения ЛОДУ второго порядка). Если два частных решения и 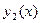ЛОДУ (1.13) образуют на интервале 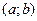фундаментальную систему, то общим решением этого уравнения является функция

, (1.16)

где и 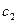произвольные постоянные.

Согласно теореме 1.2, функция (1.16) является решением уравнения (1.13). Остается доказать, что это решение общее, т. е. что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям

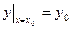, , (1.17)

где .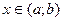

Подставив начальные условия (1.17) в решение (1.14), получим систему уравнений:

,

,

где , , с неизвестными и .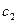

Определитель этой системы

равен значению вронскиана W(x) при .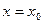

Так как решения и 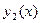образуют фундаментальную систему решений на 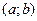и 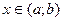, то, согласно теореме 1.4, 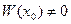. Поэтому система уравнений имеет единственное решение:

, .

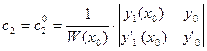Решение является частным решением (единственным, в силу теоремы единственности) уравнения (1.13), удовлетворяющим начальным условиям (1.17). Теорема доказана.

Пример 1.5. На основании теоремы 1.5 общим решением уравнения 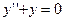(см. пример 1.4) является функция .

Дата добавления: 2015-06-04