Необходимый признак сходимости числового ряда. Гармонический ряд

Нахождение n -й частичной суммы S _n и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них, как правило, является необходимый признак сходимости.

Теорема 4.1. Если ряд (4.1) сходится, то его общий член стремится к нулю, т. е. .

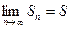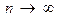Пусть ряд (4.1) сходится и . Тогда и (при и 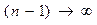). Учитывая, что 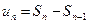при n > 1, получаем:

.

Следствие 4.1 (достаточное условие расходимости ряда). Если или этот предел не существует, то ряд расходится.

Действительно, если бы ряд сходился, то (по теореме) . Но это противоречит условию. Значит, ряд расходится.

Пример 4.2. Исследовать сходимость ряда .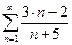

Решение: Ряд 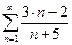расходится, т. к.

,

т. е. выполняется достаточное условие расходимости ряда.

Пример 4.3. Исследовать сходимость ряда

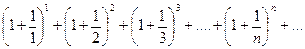
Решение: Данный ряд расходится, т. к. .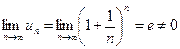

Теорема 4.1 дает необходимое условие сходимости ряда, но не достаточное: из условия не следует, что ряд сходится. Это означает, что существуют расходящиеся ряды, для которых .

В качестве примера рассмотрим так называемый гармонический ряд

(4.7)

Очевидно, что . Однако ряд (4.7) расходится. Покажем это.

Как известно (см. [1] стр.16-17), . Отсюда следует, что при любом 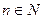имеет место неравенство . Логарифмируя это неравенство по основанию е, получим:

,

т.е.

, .

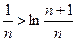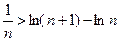Подставляя в полученное неравенство поочередно n=1, 2, …., n-1, n, получим:

,

,

,

…………………..,

.

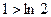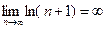Сложив почленно эти неравенства, получим . Поскольку , получаем , т. е. гармонический ряд (4.7) расходится.

В качестве второго примера можно взять ряд

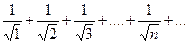
Здесь . Однако, этот ряд расходится.

Действительно,

,

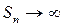т.е. . Следовательно, при 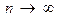, - ряд расходится.

Дата добавления: 2015-06-04