Функції із с в с. Границя, неперервність

Комплексною функцією комплексної змінної називається функція 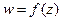, у якої область визначення 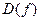та множина значень належать множині комплексних чисел . Ці функції також можна вважати як відображення із в .

Частіше за все ми будемо розглядати функції 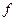, у яких областю визначення є область.

-окіл – – 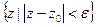відкритий круг радіуса з центром .

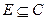Означення: Множина називається областю, якщо виконуються наступні умови:

1) кожна точка множини 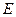– внутрішня (існує -окіл точки 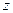, всі точки якого належать );

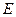2) будь-які дві точки множини 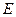можна з’єднати ламаною, всі точки якої належать .

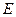Приклад області:

Однозначна функція комплексної змінної 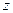, яка задана в області 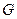, визначається законом, який ставить кожному у відповідність одне визначене комплексне число 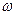. Символічно це записується .

Оскільки кожне комплексне число характеризується парою дійсних чисел, то задання комплексної функції 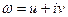комплексної змінної еквівалентне заданню двох дійсних, тобто 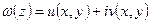, , 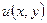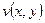визначені в області 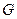. При цьому , а .

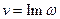Приклад: 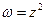, , тобто , .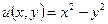

Означення: Однозначна функція 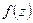називається однолистковою функцією в області 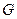, якщо в різних точках 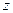цієї області вона приймає різні значення.

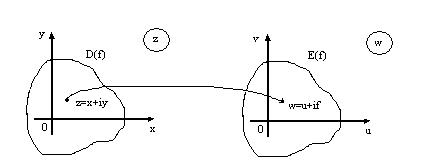
Далі ми будемо вважати, що множина – значень функції – область, тоді рівність встановлює закон відповідності між точками області 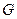площини 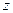і точками області площини 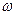. Тоді можливо встановити і обернену відповідність – кожній 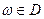ставиться у відповідність одна або декілька . Це означає, що в задана (однозначна або багатозначна) функція 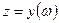– обернена 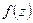. Відмітимо, що обернена функція до однолисткової функції – однозначна.

Приклад: 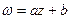, тоді обернена функція 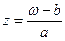однозначна функція.

Нехай 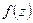визначена на області 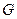, а – гранична точка .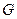

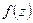Означення Коші: називається границею при 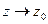, якщо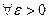 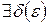таке, що 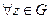і такого, що виконується нерівність

.

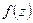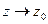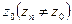Означення Гейне: називається границею при , якщо для будь-якої послідовності , яка збігається до , послідовність 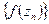збігається до . Це записується

.

Теорема: Нехай 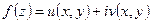, 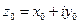гранична точка області визначення 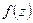. Тоді для того, щоб 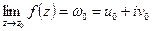необхідно і достатньо, щоб виконувались співвідношення

, .

Доведення див. [2, с. 60].

З цієї теореми слідує виконання всіх властивостей границі функції аналогічні властивостям границі дійсних функцій.

Розглянемо функцію , тоді нескінченно віддалена точка 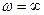визначається як точка, що відповідає початку координат 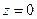при цьому .

Означення: Функція 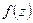називається неперервною в точці , якщо .

Неперервність 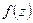в еквівалентна неперервності 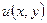, 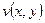в точці .

Всі властивості неперервних функцій аналогічні властивостям неперервних функцій дійсної змінної див. [2, 3]. Якщо функція неперервна в кожній точці області 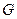, то кажуть, що вона неперервна на області .

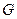Приклад 1

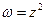. Знайти образ лінії .

Розв’язання

;

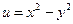
при , , .

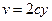Тоді або і підставляючи в отримаємо 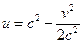– парабола. Таким чином пряма переходить при відображенні 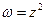в параболу .

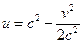Приклад 2

.

Розв’язання

.

Вправи

1. , , –?

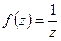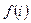2. 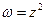. Знайти образ .

3. . Знайти образ .

4. 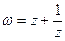. Знайти образ .

5. . Знайти образ .

6. .

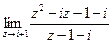7. .

8. .

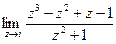9. .

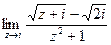10. .

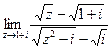Дата добавления: 2015-06-04