Геометрическая оптика и простейшие оптические приборы. Матричная оптика

Уравнение эйконала. Запишем волновое уравнение для световой волны в среде с показателем преломления n=c/ v:

. (4.1)

В общем случае для монохроматической волны справедливо:

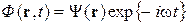. (4.2)

Подставляя (4.2) в (4.1) находим уравнение для амплитуды Y(r), зависящей только от координаты:

, (4.3)

где k ₀=w/c – волновое число в вакууме. Волновое число в среде k = nk ₀.

Воспользуемся соотношением (для других координат будет аналогично):

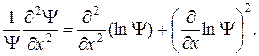(4.4)

Тогда (4.3) после деления на Y преобразуется к виду:

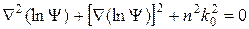. (4.5)

Решение этого уравнения ищем в виде:

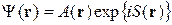. (4.6)

Вещественная скалярная функция S (r) называется эйконалом (от греческого eikon – изображение). Подставляя (4.6) в (4.5), получаем:

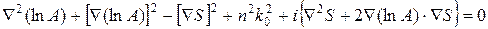. (4.7)

Приравнивая нулю вещественную и мнимую части, получим два уравнения для определения А (r) и S (r):

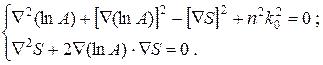(4.8)

Для оптического диапазона длина волны много меньше расстояния L, на которых амплитуда волны существенно меняется (порядка размера оптических элементов). Поэтому первыми двумя слагаемыми в первом уравнении (4.8) можно пренебречь (их сумма имеет порядок 1/ L²). Тогда это уравнение в оптическом диапазоне принимает вид уравнения эйконала:

. (4.9)

Градиент от функции S (r) направлен по нормали к поверхности S =const. Поэтому эйконал S описывает поверхности постоянной фазы волны, а Ñ S приводит к понятию луча, т.е. к представлению о движении световой энергии в данной точке в определенном направлении. Лучом называется линия, касательная к которой совпадает в каждой точке с вектором Ñ S. Распространение света рассматривается как движение световой энергии по лучам. Плоскость, перпендикулярная лучам света (где S = const), является волновым фронтом.

Анализ распространения света в лучевом приближении составляет предмет геометрической оптики. Этот подход оправдан всегда, когда

. (4.10)

Физически этот член описывает искривление материальными объектами световых лучей, т.е. дифракцию света. Исходя из этого, можно сказать, что в геометрической оптике не учитываются дифракционные эффекты (см. раздел «Дифракция света»).

Рис. 4.1

Принцип Ферма. В однородной среде S= k×r (k = const) и лучи являются прямыми параллельными линиями, а фронт волны – плоскостью, перпендикулярной лучам. Для неоднородной среды лучи имеют более сложную конфигурацию. Пусть точки P₁ и P₂ соединяются лучом L (рис.4.1). Вычислим изменение фазы вдоль луча. Для каждой его точки имеем:

, (4.11)

где d r направлен по лучу и совпадает с Ñ S, d l – элемент длины пути. Для изменения фазы находим:

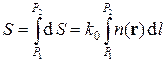. (4.12)

Интегрирование идет вдоль луча. Интеграл в (4.12) называется оптической длиной пути. Из (4.12) следует, что оптические длины путей вдоль различных лучей между точками волнового фронта в два момента времени одинаковы. Для любой другой кривой, соединяющей точки P₁ и P₂, оптическая длина пути оказывается больше, чем для реального луча.

Принцип Ферма (Fermat Pierre, 1601 – 1675) утверждает, что интеграл в (4.12) вдоль луча имеет стационарное значение, т.е. первая вариация d S относительно соседних путей интегрирования равна нулю. Или то же самое в другой формулировке: реальный луч отличается от остальных кривых, соединяющих две заданные точки, тем, что соответствующая ему оптическая длина имеет стационарное значение, т.е. малое изменение траектории не приводит к изменению оптической длины.

К принципу Ферма можно подойти и с другой стороны. Учтем что d t= d l / v – время прохождения пути d l со скоростью v, а n (r) = c / v(r). Тогда

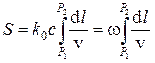, (4.13)

где интеграл здесь дает время, затрачиваемое на прохождение пути от P₁ и P₂. С этой точки зрения принцип Ферма звучит так: лучом, соединяющим две точки, является тот путь, который делает стационарным время, затрачиваемое светом на его прохождение. Формулировка о стационарности времени прохождения пути между двумя точками, с одной стороны, утверждает экстремальный характер этого времени, а с другой стороны, не исключает наличия нескольких путей с одинаковым временем прохождения.

Например, в геометрической оптике все лучи от точки предмета идут по различным путям и встречаются в точке изображения. Но все они затрачивают одно и то же время на прохождение своего пути. Другими словами, оптические длины всех путей, соединяющих точку предмета с точкой изображения, одинаковы (принцип таутохронизма).

Рис. 4.2

Вывод закона преломления из принципа Ферма. Пусть требуется соединить лучом две точки P₁ и P₂, находящиеся в однородных средах с коэффициентами преломления n₁ и n₂, разделенных плоской границей (рис. 4.2). В каждой однородной среде луч – прямая линия. Из геометрии рисунка получаем для полного времени распространения света между точками P₁ и P₂:

(4.14)

Условие стационарности 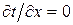принимает вид:

. (4.15)

Учитывая, что получаем соотношение, полностью совпадающее с законом Снеллиуса:

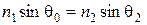. (4.16)

Распространение луча в среде с переменным коэффициентом преломления. Пусть свет распространяется в среде с аксиально-симметричным изменением коэффициента преломления. Луч распространяется вдоль положительного направления этой оси Z в параксиальном приближении. Расстояние от оси – r. Из закона Снеллиуса для бесконечно тонкого слоя D r имеем:

. (4.17)

Разложим n (r + D r) в ряд Тейлора и ограничимся линейным по D r членом:

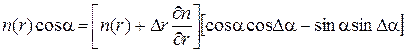. (4.18)

В параксиальном приближении sinDa» Da; cosDa» 1. Тогда с учетом линейного приближения получаем:

. (4.19)

Т.к. tga₁ = D r / D z, то в параксиальном приближении:

. (4.20)

С учетом (4.20) из (4.19) находим уравнение распространения луча:

. (4.21)

Например для диэлектрического волоконного световода n (r) =n₀ (1– ar²/ 2)и ar²/ 2«1(a> 0). Тогда уравнение (4.21) принимает вид: d² r/ d z ² = – ar. Общее решение этого уравнения гармонических колебаний в пространстве хорошо известно. Это значит, что луч внутри такого световода имеет синусоидальную траекторию.

Прохождение лучей в центрированных оптических системах. Рассмотрим прохождение лучей через сферическую линзу, не накладывая ограничений на ее толщину (рис.4.3). Обозначения видны из рисунка.

Ось Z совпадает с осью линзы. Главной оптической осью линзы называется прямая, проходящая через центры кривизны ее поверхности (в данном построении это ось Z). Свет распространяется вдоль положительного направления оси Z. Луч света лежит в плоскости XZ. r ₁ и r ₂ – радиусы кривизны 1-й и 2-й сферических поверхностей линзы (r ₂ на рис.4.3 не показан, чтобы не загромождать рисунок). Весь расчет проводится в параксиальном приближении:

(4.22)

Рис. 4.3

Преломление на первой сферической поверхности. В точке P₁ закон Снеллиуса в параксиальном приближении имеет вид:

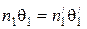. (4.23)

Используя геометрические соотношения между углами:

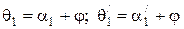, (4.24)

а в параксиальном приближении

, (4.25)

из (4.23) получаем:

. (4.26)

Кроме этого учтем соотношение

. (4.27)

Система уравнений (4.26) и (4.27) позволяют, задав координаты падающего на первую поверхность линзы луча (n ₁a₁ ; x ₁), найти координаты (n ₁^/a₁^/; x ₁^/) преломленного в линзе луча. Полученную систему удобно записать в матричном виде:

, (4.28)

где величина k₁= (n₁^/–n₁)/ r ₁ называется преломляющей силой первой поверхности, а матрица

(4.29)

называется преломляющей матрицей первой поверхности.

Распространение луча внутри линзы. Преломленный луч в параксиальном приближении, пройдя внутри линзы, падает на её вторую поверхность на расстоянии x ₂ от оси:

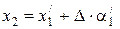. (4.30)

Отметим, что величина D в параксиальном приближении практически равна толщине линзы А₁А₂. С учетом, что получаем в матричном виде:

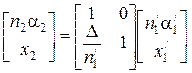. (4.31)

Матрица (4.32)

описывает распространение луча от первой поверхности линзы ко второй и называется передаточной матрицей.

Преломление луча на второй сферической поверхности рассматривается точно так же, как и на первой поверхности. Величина k₂= (n₂^/ –n₂)/ r ₂ называется преломляющей силой второй поверхности, а матрица R₂ – преломляющей матрицей второй поверхности:

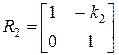. (4.33)

Знаки всех величин в приведенных выражениях необходимо брать с учётом правила знаков: если встречаемая лучом преломляющая поверхность выпуклая, то её радиус кривизны надо брать с положительным знаком, а если вогнутая – с отрицательным; углы a, отсчитываемые от оси Z против часовой стрелки, положительны, а по часовой стрелке – отрицательны; расстояния, отсчитываемые по Z (по рис. 4.3 – слева направо), положительны, а против Z (справа налево) – отрицательны; расстояния от оси Z, отсчитываемые вверх, положительны, вниз – отрицательны.

Распространение луча через оптическую систему. Используя (4.29), (4.31), (4.33), получаем связь между характеристиками на выходе линзы и входе в неё:

, (4.34)

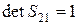, (4.35)

(4.36)

где a, b, c, d называются постоянными Гаусса. Независимыми являются только три из четырех постоянных Гаусса. Матрица S ₂₁ полностью описывает рассмотренную оптическую систему.

Преобразование луча от плоскости предмета к плоскости изображения. Пусть из точки некоторой плоскости (плоскости предмета), расположенной на расстоянии l слева от точки А ₁ выходит луч с координатами (n₁ a ₁, x) и падает на рассматриваемую линзу. В некоторой плоскости, расположенной справа от точки А ₂ на расстоянии l ^/ луч характеризуется координатами (n₂^/ a ₂^/, x ^/). Между этими парами координат по приведенным выше правилам получаем соотношение:

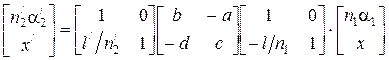. (4.37)

Перемножая матрицы в (4.37), имеем:

. (4.38)

Матрица Q₂₁ называется матрицей преобразования предмета к изображению:

. (4.39)

Обозначим 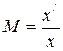– увеличение оптической системы. (4.40)

Введем понятие изображения. Под изображением понимается такое отображение плоскости предмета на плоскость, называемую плоскостью изображения, когда все лучи, выходящие из точки предмета, сходятся после преломления в оптической системе в одной точке плоскости изображения, и все точки отображаются с одинаковым увеличением.

Исходя из этого определения в точке изображения увеличение М не должно зависеть от угла a₁. Поэтому соответствующий член в матрице Q ₂₁ обращается в нуль:

. (4.41)

Из определения увеличения и выражения (4.40) имеем:

. (4.42)

Тогда матрица преобразования от предмета к изображению принимает вид:

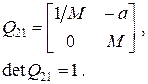(4.43)

Кардинальные элементы оптической системы. Плоскости H и H ^/, увеличение для точек которых М = 1, называются главными плоскостями, а их пересечения с осью системы (ось Z) – главными точками системы. Найдём из (4.42) их положение:

, (4.44)

где l _H – отсчёт положения плоскости H относительно точки А ₁; l _H^/ – отсчёт положения плоскости H^/ относительно точки А ₂ .

Точка на оси системы, в которой сходятся лучи, падающие на оптическую систему параллельно оптической оси (т.е. точка с увеличением M = 0) и точка, выйдя из которой лучи после прохождения оптической системы становятся параллельными оптической оси (т.е. с увеличением M = ¥), называются фокусами оптической системы. Плоскости, проходящие через фокусы перпендикулярно оптической оси, называются фокальными. Найдём из (4.42) их положение:

(4.45)

где l_F – отсчёт положения переднего фокуса относительно точки А ₁, l _F^/ – отсчёт положения заднего фокуса относительно точки А ₂.

Расстояние f между передней главной точкой и передним фокусом называется передним фокусным расстоянием; расстояние f ^/между задней главной точкой и задним фокусом называется задним фокусным расстоянием:

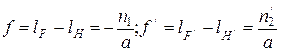. (4.46)

Главные и фокальные плоскости называются кардинальными элементами оптической системы. Их положение позволяет полностью описать преломление лучей в оптической системе и построить изображение заданного предмета (рис.4.4).

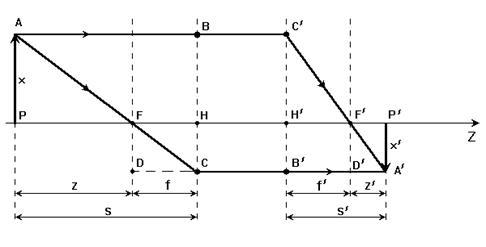Рис. 4.4

Физический смысл постоянных Гаусса. Пусть линза располагается в воздухе: n ₁ = n ₂^/ = 1. Тогда из (4.46) следует:

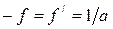, (4.47)

т.е. a является величиной, обратной фокусному расстоянию. Из (4.45) и (4.47) имеем:

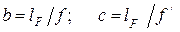. (4.48)

Коэффициенты b и c характеризуют взаимное расположение главных и фокальных плоскостей.

Уравнение линзы. Из подобия треугольников CDF, ABC, FPA (рис.4.4) следует:

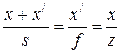, (4.49)

а из подобия треугольников A^/D^/F^/, F^/H^/C^/, A^/B^/C^/ следует:

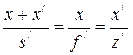. (4.50)

Из этих соотношений имеем:

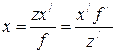, (4.51)

а отсюда получаем уравнение линзы в форме Ньютона:

. (4.52)

Из этих же уравнений можно получить уравнение линзы в форме Гаусса:

. (4.53)

Увеличение линзы определяется из формулы:

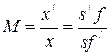. (4.54)

Тонкие линзы. Пусть 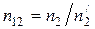– относительный коэффициент преломления и 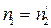. Тогда из (4.36) и (4.47) следует выражение для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры:

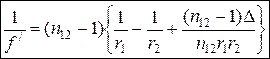. (4.55)

Тонкой линзой называется линза, для которых можно пренебречь третьим слагаемым в скобках (4.55), что соответствует малости толщины линзы по сравнению с каждым радиусом кривизны:

. (4.56)

Тонкая линза представляется не имеющей толщины и с ней совпадают обе главные плоскости. Фокусное расстояние становится равным отсчёту от линзы до фокуса. При этом условии матрица с коэффициентами Гаусса для тонкой линзы принимает вид:

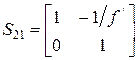. (4.57)

Величина 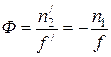(4.58)

называется оптической силой линзы. Оптическая сила измеряется в диоптриях (1 дптр соответствует фокусному расстоянию в 1 м). Оптическая сила положительна для собирающих линз и отрицательна для рассеивающих.

Рассмотрим в качестве примера простейшую систему из двух тонких линз (рис. 4.5). Тогда матрица S (4.34), описывающая данную систему будет получаться из результата перемножения матриц:

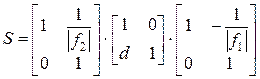. (4.59)

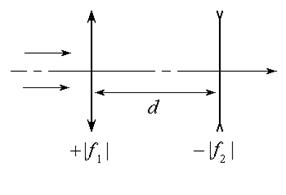Рис. 4.5

Далее находятся постоянные Гаусса, а из них кардинальные элементы данной оптической системы. Отсчет для передних главной точки и фокуса идет от передней линзы, а для задних кардинальных точек – от последней линзы по приведенному выше правилу знаков.

Отражение от сферических поверхностей рассматривается как преломление в среду с отрицательным показателем преломления – n, если n – показатель преломления среды, из которой луч падает на отражающую поверхность. В остальном матрица, описывающая отражение, полностью аналогична матрице, описывающей преломление. Правило знаков остается тем же.

Аберрации оптических систем. В определении понятия изображения содержится требование того, чтобы все лучи, выходящие из точки предмета, сходились в одной и той же точке в плоскости изображения, при этом увеличение для всех точек предмета остается постоянным. Отклонения фактически получаемого изображения от идеального, описываемого всеми предыдущими формулами, называются аберрациями. Для параксиальных лучей аберрации малы и ими пренебрегают. Если же лучи не параксиальные, то аберрации становятся значительными и сильно искажают изображение.

Первый источник аберраций состоит в том, что линзы, ограниченные сферическими поверхностями, преломляют лучи не совсем так, как это принимается в параксиальном приближении (например, фокусы для лучей, падающих на разных расстояниях от оси линзы, различны.). Такие аберрации называются геометрическими (монохроматическими).

Например, параксиальное приближение основывается на линейном разложении синуса в ряд. Неучтенные в таком приближении члены ~a³, ~a⁵ и т.д. приводят к аберрациям третьего, пятого и т.д. порядков.

К геометрическим аберрациям относятся:

1. Сферическая аберрация.

2. Кома.

3. Астигматизм.

4. Искривление поверхности изображения (кривизна поля).

5. Дисторсия.

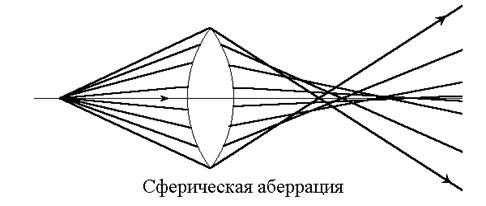Рис. 4.6

При сферической аберрации лучи, параллельные оптической оси, не пересекаются после линзы в одной точке. Пучок параллельных оси лучей после преломления образует совокупность конусов, вершины которых расположены на оси. Огибающая эту совокупность конусов поверхность называется каустической, а сечение этой поверхности любой плоскостью, проходящей через луч – каустической кривой (рис.4.6).

Если светящаяся точка расположена не на оптической оси, то её изображение не является светящимся кружком, как в предыдущем случае, а представляется в виде довольно сложной асимметричной фигуры, напоминающей комету с хвостом. Такая аберрация называется комой.

Если на линзу падает цилиндрический пучок лучей под достаточно большим углом к оптической оси, то в результате сечение пучка лучей изменяется с расстоянием от линзы после преломления (рис.4.7). На некотором расстоянии от линзы сечение является отрезком линии, перпендикулярным плоскости падения пучка (такая плоскость падения, образованная осью падения пучка и оптической осью, называется меридианальной плоскостью, а перпендикулярная ей – сагиттальной). Затем эта линия переходит в эллипс, на некотором расстоянии дальше сечение опять становится круговым, а затем эллиптическим и дальше превращается в отрезок линии, лежащей в меридианальной плоскости. Такой вид аберрации называется астигматизмом.

Рис. 4.7

Поверхности, на которых лежат фокусы (где образуются отрезки линий при астигматизме), создаваемые меридианальной и сагиттальной фокусировками, не совпадают между собой и не являются плоскостями. Эти поверхности касаются лишь в точке F^/ оптической оси. Этот вид аберрации называется искривлениемповерхностиизображения.

Увеличение системы, вообще говоря, зависит от угла наклона падающих лучей. В результате, например, сетка из прямых линий превращается в сетку из кривых линий. Такая аберрация называется дисторсией (рис.4.8).

Рис. 4.8

Второй источник аберраций связан с дисперсией света. Т.к. показатель преломления зависит от частоты, то и фокусное расстояние и другие характеристики системы зависят от частоты. Поэтому лучи, соответствующие излучению различной частоты, исходящие из одной точки предмета, не сходятся в одной точке изображения даже в идеальном случае. Такие аберрации называются хроматическими.

Некоторые приборы геометрической оптики.

1. Глаз. (рис.4.9)

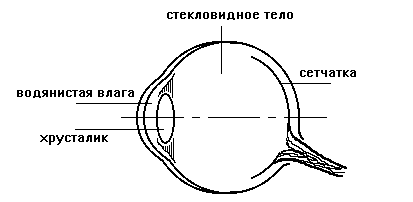Рис. 4.9

Фокусировка глаза на предмет называется аккомодацией.

Средние характеристики человеческого глаза:

Оптическая сила ~ 58 дптр.

Длина глаза ~ 22 мм.

Радиус кривизны

сетчатки ~ 9,7 мм;

преломляющей

поверхности ~ 5,6 мм.

Показатель преломления

среды 1,33;

хрусталика ~ 1,4 – 1,45.

Расстояние наилучшего зрения 25 см.

2. Линзовый телескоп (рис.4.10). Увеличение (4.60)

Рис. 4.10

3. Лупа. Простейшая оптическая система с малым фокусным расстоянием (~1 см или немного больше). Предмет располагается на расстоянии от лупы меньше фокусного. Изображение мнимое, прямое, увеличенное. Увеличение

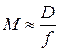, (4.61)

где D – расстояние наилучшего зрения (25 см).

4. Микроскоп. Передняя собирающая линза называется объективом (f ₁ около сантиметра), задняя – окуляром (f ₂ около нескольких сантиметров). Объектив строит увеличенное перевернутое действительное изображение, окуляр играет роль лупы для этого изображения как предмета. Увеличение

, (4.62)

где d – расстояние между фокусами объектива и окуляра.

Дата добавления: 2015-06-04