
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статистические методы проверки гипотез
|
|
|
|
Понятие статистической гипотезы.
Cтатистическая гипотеза – это различного рода предположения относительно характеристик, вида или параметров распределения случайной переменной, которые можно проверить по результатам наблюдений в случайной выборке. Обозначается гипотеза Н от латинского слова hypothesis. Типичные примеры статистических гипотез: а) средние значения переменной в двух генеральных совокупностях различаются; б) переменная имеет в генеральной совокупности данное распределение (например, Пуассона).
Гипотеза «на Марсе есть жизнь» не является статистической, т.к. в ней не идет речь ни о виде, ни о параметрах распределения.
Виды гипотез:
Нулевой (основной) называют выдвинутую гипотезу, обозначают ее Н 0.
Конкурирующей (альтернативной) называют гипотезу, которая противоречит нулевой, обозначают ее Н 1. Ее принимают, если нулевая гипотеза неверна.
Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10 (Н 0: а =10), то конкурирующая гипотеза, в частности, может быть следующей: Н 1: а ¹10.
Простой называют гипотезу, содержащую только одно предположение. Например, если l - параметр показательного распределения, то гипотеза Н0: l =5 – простая.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Например, сложная гипотеза Н: l >5 состоит из бесконечного множества простых гипотез вида Н: l = bi, где bi - любое число, большее 5. (Н: l =6, l =7, l =8 и т.д.).
Гипотеза Х ср1= Х ср2 также является сложной: ее можно рассматривать как объединение простых гипотез о распределениях в обеих совокупностях с совпадающими средними значениями. (Хср1=Хср2=10; Хср1=Хср2=25 и т.д.)
|
|
|
Как сама проверяемая гипотеза Н 0, так и конкурирующая ей, могут быть простыми либо сложными, так что в этом отношении можно выделить 4 типа проверки гипотез: «Н 0:простая гипотеза против Н 1:простой», «Н 0:простая против Н 1:сложной», «Н 0:сложная против Н 1:простой», «Н 0:сложная против Н 1:сложной». Наиболее распространенный случай «Н 0:простая против Н 1:сложной».
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В результате проверки гипотеза Н 0 может быть отвергнута или не отвергнута. Отвергают гипотезу категоричнее, чем принимают.
Основное правило статистической проверки гипотезы - критерий проверки гипотезы включает следующие элементы: статистику критерия, уровень значимости, критическую область.
Статистика критерия – это функция S (X) от распределения случайной величины Х в выборке, представляющая собой специально-подобранную случайную величину, точное или приближенное распределение которой известно и которая служит для проверки нулевой гипотезы Н 0.
S (X)= f (X 1,.., Xn). От выборки к выборке значения S (X) меняются и S (X) сама может быть рассмотрена как случайная величина.
Эта величина в зависимости от вида распределения может иметь специальные обозначения. Так, если она распределена нормально, ее обозначают U или Z, если она распределена по закону Стьюдента - T, если она распределена по закону «хи-квадрат» - c 2, если она распределена по закону Фишера-Снедокорра – F.
Наблюдаемым значением статистики критерия S набл называют значение S (X), вычисленное по имеющейся в нашем распоряжении выборке.
Значение статистики критерия зависит от: 1) данных выборки, т.е. от Х =(Х 1, Х 2,…, Хn); 2) вида гипотезы Н 0, который определяет вид функции f (формулу расчета статистики критерия).
|
|
|
Критической областью m 1 называется – совокупность значений статистики критерия S (X), при которых нулевую гипотезу отклоняют.
Областью принятия гипотезы (допустимых значений) m 0 называется совокупность значений статистики критерия S (X), при которых нулевую гипотезу не отклоняют.
Поскольку статистика критерия — одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.
Критические точки (границы) S кр– точки, отделяющие критическую область от области принятия гипотезы.
Различают критическую область одностороннюю (правостороннюю и левостороннюю) и двустороннюю.
Правосторонняя критическая область определяется неравенством: S (X)> S кр
 m 0
m 0  m 1
m 1
 S кр
S кр
Левосторонняя критическая область определяется неравенством: S (X)< S кр
 m 1
m 1  m 0
m 0
 S кр
S кр
Двусторонняя критическая область определяется неравенствами: S (X)> S кр2 и S (X)< S кр1

 m 1 m 0 m 1
m 1 m 0 m 1
 S кр1 S кр2
S кр1 S кр2
Основное правило статистической проверки гипотезы можно сформулировать так: если наблюдаемое по выборке значение статистики критерия S набл принадлежит критической области (m 1), то гипотезу Н 0 отвергают; если S набл принадлежит области принятия гипотезы (m 0), то гипотезу Н 0 не отвергают.
| Вид критической области | Условие не отклонения Н 0 | Условие отклонения Н 0 |
| Правосторонняя | S набл< S кр | S набл> S кр |
| Левосторонняя | S набл> S кр | S набл< S кр |
| Двусторонняя | S кр1< S набл< S кр2 | S набл> S кр2 и S набл< S кр1 |
Следование этому правилу может привести к ошибкам двоякого рода:
а) ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза Н 0, а принята Н 1. Вероятность совершить ошибку первого рода принято обозначать через a, ее называют уровнем значимости. (a = Р [ S наблÎ m 1½ Н 0]). Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Например, если при Н 0: новое минеральное удобрение лучше, установлено, что новое минеральное не лучше, хотя на самом деле это не так.
б) ошибка второго рода состоит в том, что будет принята неправильная гипотеза, т.е. принята гипотеза Н 0, в то время как она неверна в действительности. Вероятность такой ошибки обозначают - b = Р [ S наблÎ m 0½ Н 1]. Например, если мы решили, что новое удобрение лучше старого, хотя на самом деле это не так.
|
|
|
Правильное решение может быть принято также в двух случаях:
1) Гипотеза принимается, причем и в действительности она правильная. Вероятность такого события есть доверительная вероятность, которая равна 1- a.
2) Гипотеза отвергается, причем и в действительности она неверна. Вероятность такого события называют мощностью критерия, она равна 1- b.
Чем меньше вероятности ошибок 1-ого и 2-ого родов, тем лучше. Но одновременно уменьшить a и b практически невозможно. Обычно поступают так: задаются уровнем вероятности одной из ошибок (чаще a) и пытаются максимально уменьшить вероятность другой ошибки. Единственный способ одновременного уменьшения a и b состоит в увеличении объема выборки.
Рассмотрим, как определяется критическая область (критические точки), когда Н 0 -простая гипотеза, а Н 1 - сложная.
Задача отыскания S кр ставится так:
а) при правосторонней критической области: по заданному уровню значимости a найти S кр, удовлетворяющую равенству: P (S (X)> S крê H 0)= a;
б) при левосторонней критической области: по заданному уровню значимости a найти S кр, удовлетворяющую равенству: P (S (X)< S крê H 0)= a;
в) при двусторонней критической области: по заданному уровню значимости a найти S кр, удовлетворяющую равенству: P (S (X)< S кр1 ê H 0)+ P (S (X)> S кр2ê H 0)= a.
Для каждого вида статистики критерия S (X) имеются свои таблицы, по которым и находят критическую точку S кр при заданном уровне значимости a.
Пусть S (X) распределена по нормальному закону, тогда выбор S кр можно представить:
а) для правосторонней критической области рисунком 7.1 (а);
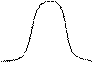
б) для левосторонней критической области рисунком 7.1 (б);
в) для двусторонней критической области рисунком 7.1 (в).
a  на рисунке соответствует площади под кривой f (S | H 0).
на рисунке соответствует площади под кривой f (S | H 0).



 f (S)
f (S)
 |


 a m 1 S a)
a m 1 S a) 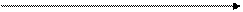 f (S | H 0) f (S | H 1)
f (S | H 0) f (S | H 1)
S кр
 |


 f(S)
f(S)
 m 1 a S кр S б)
m 1 a S кр S б)
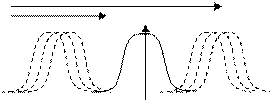

 m 1 a /2 a /2 m 1 S в)
m 1 a /2 a /2 m 1 S в)
|
|
|
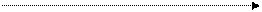 - S кр S кр
- S кр S кр
 |  |
В случае двусторонней критической области критические точки могут быть выбраны бесчисленным множеством способов. Если же распределения статистики критерия симметрично относительно нуля и имеются основания (например, для увеличения мощности критерия или уменьшения b) выбрать симметричные относительно нуля точки - S кр и S кр, то:
P (S (X)<- S кр ê H 0) = P (S (X)> S крê H 0),
следовательно, P (S (X)> S крê H 0)= a /2. Это соотношение и служит для отыскания критических точек двусторонней критической области.
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 1406; Нарушение авторских прав?; Мы поможем в написании вашей работы!