
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Касательные напряжения при поперечном изгибе. Главные напряжения при изгибе 1 страница
|
|
|
|
Схема III. Плоская рама (задача № 8)
Схема I. Консольная балка (задача №6)
Решение
Примеры расчетов
Для статически определимых систем: схемы I (консольная балка, рис. 5.8, а), схемы II (двухопорная балка с консолями, рис. 5.13) и схемы III (плоской рамы в виде ломаного бруса, рис. 5.17) при последовательном их рассмотрении требуется:
1. Построить эпюры Mx и Qy для всех схем и эпюру Nz для схемы III;
2. Руководствуясь эпюрой Mx, показать на схемах I и II приблизительный вид изогнутой оси балки. По опасному сечению подобрать размеры поперечного сечения:
а) для схемы I - прямоугольное h ´ b при расчетном сопротивлении RH = 16×103 кН/м2 (клееная древесина); h: b = 1,5;
б) для схемы II - двутавровое (ГОСТ 8239-72) при расчетном сопротивлении RH = 200×103 кН/м2 (сталь);
Учитывая особенности рассматриваемой системы (рис. 5.8, а), чтобы исключить необходимость определения опорных реакций, достаточно применяя метод сечений, последовательно рассмотреть те отсеченные части системы от заданного сечения, в котором отсутствует опорное сечение.
1. Построить эпюры Qy и Mx. Для построения эпюр Qy и Mx определяем количество участков, затем, используя метод сечений, составляем аналитические выражения изменения Qy и Mx в зависимости от текущей абсциссы z для каждого участка.

|
Рис. 5.8
Определение количества участков балки
Границами между двумя смежными участками, как правило, являются места расположения тех сечений, где происходит скачкообразное изменение: физико-механических характеристик материала конструкций; геометрических характеристик поперечных сечений (формы и/или размеров), а также внешних нагрузок. В данном случае, рассматриваемая балка, имеющая постоянное поперечное сечение (рис. 5.8, б) имеет три участка: участок I - DС, участок II - СВ, участок III - ВА.
|
|
|
Составление аналитических выражений Qy и Mx и определение значений в характерных сечениях
Проведя сечение I-I, рассмотрим равновесие правой отсеченной части балки длиной z 1, приложив к ней все действующие справа от сечения заданные нагрузки и внутренние силовые факторы Qy и Mx , возникающие в сечении, которые заменяют действие отброшенной части балки (рис. 5.9). При этом, предполагаем, что изображенные на рисунке внутренние силовые факторы положительны.
Составив уравнения равновесия S y = 0 и 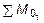 = 0 для этой части балки и решив их, найдем выражения для
= 0 для этой части балки и решив их, найдем выражения для  и
и 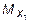 в зависимости от z 1 на участке I (0 £ z 1 £ 1 м):
в зависимости от z 1 на участке I (0 £ z 1 £ 1 м):
 S y = 0,
S y = 0,  = 0;
= 0;
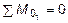 ,
, 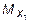 + m = 0,
+ m = 0, 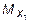 = - m = -10 кН×м.
= - m = -10 кН×м.
Полученные выражения показывают, что на участке I  и
и 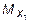 - const. Знак “минус” у
- const. Знак “минус” у 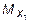 говорит о том, что момент в сечении I-I вызывает растяжение верхних, а не нижних волокон, как это показано на рис. 5.9.
говорит о том, что момент в сечении I-I вызывает растяжение верхних, а не нижних волокон, как это показано на рис. 5.9.

|
Участок II (1 м £ z 2 £ 2 м).
Составим уравнения S y = 0 и 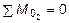 для отсеченной сечением II-II правой части балки (рис. 5.10) и определим из них
для отсеченной сечением II-II правой части балки (рис. 5.10) и определим из них 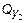 и
и 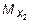 :
:
S y = 0,  кН;
кН;
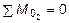 ,
, 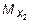 + m - P (z 2 - 1) = 0,
+ m - P (z 2 - 1) = 0, 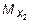 = - m + P (z 2 - 1).
= - m + P (z 2 - 1).
Из полученных выражений для 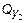 и
и 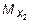 видно, что на участке II величина
видно, что на участке II величина 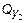 постоянна, а величина
постоянна, а величина 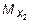 изменяется в зависимости от z 2 по закону прямой линии. Знак “минус” у
изменяется в зависимости от z 2 по закону прямой линии. Знак “минус” у 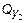 показывает, что в сечении II-II возникает поперечная сила, действующая в направлении, обратном показанному на рис. 5.10.
показывает, что в сечении II-II возникает поперечная сила, действующая в направлении, обратном показанному на рис. 5.10.
Теперь, подставляя значения z 2 для характерных сечений участка II в полученные аналитические выражения, определим величины 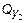 и
и 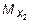 , возникающие в этих сечениях, т.е. ординаты эпюр Mx и Qy в точках С и В (рис. 5.8, б).
, возникающие в этих сечениях, т.е. ординаты эпюр Mx и Qy в точках С и В (рис. 5.8, б).
при z 2 = 1 м; 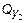 = -30 кН;
= -30 кН; 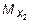 = -10 + 30 (1 - 1) = -10 кН×м;
= -10 + 30 (1 - 1) = -10 кН×м;
при z 2 = 2 м; 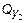 = -30 кН;
= -30 кН; 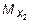 = -10 + 30 (2 - 1) = 20 кН×м.
= -10 + 30 (2 - 1) = 20 кН×м.
Участок III (2 м £ z 2 £ 4 м).
Составим уравнения равновесия S y = 0 и  для отсеченной сечением III-III правой части балки (рис. 5.11) и, решив их, получим,
для отсеченной сечением III-III правой части балки (рис. 5.11) и, решив их, получим,
S y = 0, 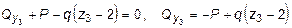 ;
;
 ,
,  + m - P (z 3 - 1) + 0,5 q (z 2 - 2)2 = 0,
+ m - P (z 3 - 1) + 0,5 q (z 2 - 2)2 = 0,
|
|
|
 = - m + P (z 3 - 1) - 0,5 q (z 2 - 2)2.
= - m + P (z 3 - 1) - 0,5 q (z 2 - 2)2.
Таким образом, величина 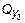 на участке III изменяется по закону прямой линии, а величина
на участке III изменяется по закону прямой линии, а величина  - по закону квадратной параболы.
- по закону квадратной параболы.
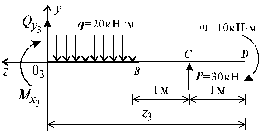 Рис. 5.11
Рис. 5.11
|
Подставив значения z 3 , соответствующие характерным сечениям участка, в аналитические выражения изменения 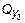 и
и  , определим координаты эпюр для сечений В и А (рис. 5.8, б).
, определим координаты эпюр для сечений В и А (рис. 5.8, б).
При z 3 = 2 м 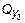 = -30 + 20×(2 - 2) = - 30 кН;
= -30 + 20×(2 - 2) = - 30 кН;
 = -10 + 30 (2 - 1) - 0,5×20×(2 - 2)2 = 20 кН×м.
= -10 + 30 (2 - 1) - 0,5×20×(2 - 2)2 = 20 кН×м.
При z 3 = 4 м 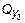 = -30 + 20×(4 - 2) = 10 кН;
= -30 + 20×(4 - 2) = 10 кН;
 = -10 + 30 (4 - 1) - 0,5×20×(4 - 2)2 = 40 кН×м.
= -10 + 30 (4 - 1) - 0,5×20×(4 - 2)2 = 40 кН×м.
Так как, поперечная сила в пределах участка меняет знак, т.е. имеет промежуточное нулевое значение (рис. 5.8, в), то в этом сечении возникает экстремальное значение изгибающего момента. Для определения его величины вначале найдем значение z 0, при котором 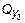 = 0. Для этого, приравняв выражение для
= 0. Для этого, приравняв выражение для 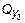 нулю, получим:
нулю, получим:
- P + q (z 0 - 2) = 0, 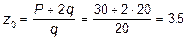 м.
м.
Подставив найденное значение z 0 = 3,5 м в аналитическое выражение изменения  , вычислим величину M max:
, вычислим величину M max:
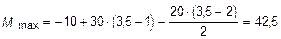 кН×м.
кН×м.
Построение эпюр Qy и Mx для всей балки
Отложив перпендикулярно к оси абсцисс (линии, параллельной оси балки) в удобном для пользования масштабе вычисленные значения Qy и Mx в характерных и промежуточных сечениях каждого участка и соединяя концы полученных ординат линиями, соответствующими законам изменения Qy и Mx на каждом участке, построим эпюры Qy и Mx для всей балки (рис. 5.8, в, г). При этом положительные ординаты эпюры Qy откладываются вверх, а отрицательные - вниз по оси абсцисс. Ординаты же эпюр Mx откладываются со стороны растянутого волокна. На эпюрах Qy обязательно указываются знаки, а на эпюре Mx знаки можно не ставить.
Проверка правильности построения эпюр Qy и Mx
 Рис. 5.12
Рис. 5.12
|
Для этого необходимо вначале проверить соответствие эпюры Qy эпюре Mx согласно дифференциальной зависимости 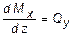 , из которой следует, что эпюра Qy представляет собой эпюру тангенсов угла наклона касательных эпюры Mx к оси балки. В самом деле, на участке II балки (рис. 5.8, г) тангенс угла наклона касательной эпюры Mx к оси балки (рис. 5.12) равен:
, из которой следует, что эпюра Qy представляет собой эпюру тангенсов угла наклона касательных эпюры Mx к оси балки. В самом деле, на участке II балки (рис. 5.8, г) тангенс угла наклона касательной эпюры Mx к оси балки (рис. 5.12) равен:
 кН.
кН.
При этом, знак поперечной силы будет положительным, если угол образован вращением оси балки или элемента системы по ходу часовой стрелки, и отрицательным, если угол образован вращением этой оси против часовой стрелки до совмещения с эпюрой Mx .
|
|
|
В рассматриваемом примере угол a образован вращением оси балки против часовой стрелки, поэтому поперечная сила на этом участке будет отрицательной. После указанной проверки полезно также проверить выполнение следующих положений:
1. Эпюра Mx на участке между сосредоточенными силами, а также между сосредоточенными силой и моментом, и между началом или концом действия равномерно распределенной нагрузки и сосредоточенными силой и моментом всегда изменяется по закону прямой линии, наклонной к оси элемента, а в пределах действия равномерно распределенной нагрузки по закону квадратной параболы, имеющей выпуклость в сторону ее действия, если эпюра построена со стороны растянутого волокна;
2. Под точкой приложения сосредоточенной силы эпюра Mx имеет излом, острие которого направлено в сторону действия силы, если эпюра построена со стороны растянутого волокна;
3. На эпюре Mx в месте действия сосредоточенного момента m имеет место скачок, равный его величине;
4. Над шарнирными опорами двухшарнирной балки изгибающий момент может быть только в тех случаях, когда в опорных сечениях приложены сосредоточенные моменты или когда на консолях, расположенных за опорами, приложены нагрузки. Во всех других случаях изгибающие моменты в шарнирах равны нулю;
5. На участке действия равномерно распределенной нагрузки изгибающий момент достигает экстремального значения Mx =
= M max в том сечении, где поперечная сила 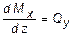 , т.е. переходит через нуль, меняя знак;
, т.е. переходит через нуль, меняя знак;
6. Поперечная сила Qy на участке равна нулю, если во всех сечениях по длине этого участка Mx = const;
7. Эпюра Qy постоянна на участках между сосредоточенными нагрузками и изменяется по закону наклонной прямой лишь на участках, где действует равномерно распределенная нагрузка;
8. Эпюра Qy в точках приложения сосредоточенных вертикальных сил (Р, RA , RB) имеет скачки, равные по величине приложенным в этих сечениях сосредоточенным силам, причем направление скачков всегда совпадает с направлением этих сил.
В нашем примере все эти положения выполняются.
|
|
|
2.1. Руководствуясь эпюрой Mx, показать приблизительный вид изогнутой оси балки. При построении приблизительного вида изогнутой оси балки по эпюре Mx необходимо знать, что знак изгибающего момента связан с характером деформации балки от действия заданной внешней нагрузки. Если на участке балки изгибающий момент положителен, то балка на этом участке изгибается выпуклостью вниз, а если отрицателен - выпуклостью вверх. В тех же сечениях, где изгибающий момент равен нулю, кривизна балки меняет свой знак, т.е. ось балки в этих сечениях имеет точки перегиба. При этом всегда следует помнить, что прогибы балки на опорах равны нулю.
Анализируя эпюру Mx (рис. 5.8, г), видим, что на участке АО растянуты нижние волокна, значит, на этом участке изогнутая ось балки будет иметь выпуклость вниз. На участке ОД растянуты верхние волокна, поэтому изогнутая ось балки на этом участке будет иметь выпуклость вверх. Таким образом, под точкой О, где Mx = 0, кривизна изогнутой оси балки меняет знак, т.е. упругая линия имеет в этом сечении точку перегиба. Учитывая это, строим приблизительный вид изогнутой оси балки (рис. 5.8, д).
2.2. Подбор поперечного сечения балки. Опасным сечением является то, в котором возникает наибольший по абсолютной величине изгибающий момент. В нашем примере опасным является сечение Е, где M max = 42,5 кН×м. Прямоугольное сечение балки из клееной древесины подбираем из условия прочности при расчетном сопротивлении RH = 16×103 кН/м2 и соотношения h / b = 1,5:
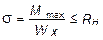 ,
,
откуда требуемый момент сопротивления сечения балки при изгибе будет равен:
 = 2,66×10-3 м3.
= 2,66×10-3 м3.
Момент сопротивления прямоугольного сечения равен:
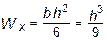 .
.
Приравняв его 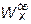 , получим
, получим  =
=
= 0,288 м, тогда:
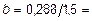 0,192 м.
0,192 м.
Округляя, принимаем брус поперечным сечением h ´ b = 0,29´ ´0,19 м2, (Wx = 2,663×10-3м3).
5.4.2. Схема II. Двухопорная балка (задача № 7)
1. Построить эпюры Qy и Mx. Существенное отличие этой схемы (рис. 5.13, а) от предыдущего примера расчета (рис. 5.8, а) заключается в том, что при рассмотрении однопролетной консольной балки, для определения внутренних силовых факторов с применением метода сечений, мы последовательно рассматривали равновесие той части системы, где отсутствовало опорное сечение. Данное обстоятельство позволило без предварительного определения опорных реакций, вычислить значения внутренних усилий. Так как этот прием, в данном случае, нереализуем, поэтому предварительно необходимо определить полную систему внешних сил, которая включает заданную систему и все опорные реакции.
Определение опорных реакций
При общем случае нагружения в заданной системе возникают три опорные реакции. Однако, учитывая особенности характера нагружения, т.е. все внешние силы направлены по оси y, поэтому можно утверждать, что горизонтальная опорная реакция в опорном сечении А в данном случае равна нулю. Вертикальные опорные реакции могут быть определены из условий S MA = 0; S MB = 0.
Необходимым и достаточным условием проверки правильности определения вертикальных опорных реакций является S y = 0, т.к. это уравнение статики, применительно к рассматриваемой системе, которое содержит все искомые опорные реакции.
Из S MA = 0 получим:
S MA = - Р ×1 + q ×5×4,5 - m - RB ×6 = 0,
откуда
 кН.
кН.
Из уравнения S MB = 0 будем иметь:
S MB = - P ×7 - m - q ×5×1,5 + RA ×6 =0; RA = 40 кН.
Опорные реакции RA и RB получились положительными. Это означает, что выбранные направления совпадают с их действительными направлениями. После определения опорных реакций следует провести проверку правильности их вычисления.

|
Рис. 5.13
S y = - P - q ×5 + RA + RB = 0; -10 - 20×5 + 40 + 70 = 0;
-110 + 110 = 0; 0 = 0.
Удовлетворение этого уравнения говорит о правильности вычисления величин и направления опорных реакций.
Определение количества участков
Учитывая, что границами участков являются точки приложения внешних сил и опорных реакций, а также сечения, где распределенная нагрузка меняется скачкообразно. Поэтому заданная балка имеет четыре участка: I участок - КА; II участок - АС; III участок - СВ и IV участок - ВD (рис. 5.13, б).
Составление аналитических выражений Qy, Mx и определение значений их в характерных сечениях каждого участка
Поместив начало системы координат в центре тяжести крайнего левого поперечного сечения балки, и рассекая ее в пределах участка I, рассмотрим равновесие левой части балки длиной z 1 (рис. 5.14, а). Составив уравнения равновесия S y = 0 и 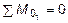 для этой части, найдем аналитические выражения изменения Qy и Mx на участке I, где z 1 изменяется в пределах 0 £ z 1 £ 1 м:
для этой части, найдем аналитические выражения изменения Qy и Mx на участке I, где z 1 изменяется в пределах 0 £ z 1 £ 1 м:

|
Рис. 5.14
S y = 0, -  - P = 0,
- P = 0,  = - P (постоянная величина);
= - P (постоянная величина);
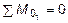 , -
, - 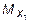 - P × z 1 = 0,
- P × z 1 = 0, 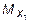 = - P × z 1 (уравнение прямой линии).
= - P × z 1 (уравнение прямой линии).
Знак “минус” у  говорит о том, что в этом сечении возникает поперечная сила, действующая в направлении, обратном показанному на рис. 5.14, а, а у
говорит о том, что в этом сечении возникает поперечная сила, действующая в направлении, обратном показанному на рис. 5.14, а, а у 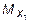 - что в сечении будет возникать изгибающий момент, растягивающий верхние волокна, а не нижние, как показано на рис. 5.14, а. Для определения величин
- что в сечении будет возникать изгибающий момент, растягивающий верхние волокна, а не нижние, как показано на рис. 5.14, а. Для определения величин  и
и 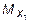 в характерных сечениях этого участка подставим значения z 1 в полученные аналитические выражения:
в характерных сечениях этого участка подставим значения z 1 в полученные аналитические выражения:
при z 1 = 0  = -10 кН,
= -10 кН, 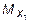 = -10×0 = 0;
= -10×0 = 0;
при z 1 = 1 м  = -10 кН,
= -10 кН, 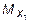 = -10×1 = -10кН×м.
= -10×1 = -10кН×м.
Проведя сечение в пределах участка II, рассмотрим равновесие левой отсеченной части балки (рис. 5.14, б) и из уравнений равновесия S y = 0 и 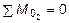 найдем аналитические выражения для
найдем аналитические выражения для 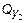 и
и 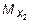 на этом участке, где z 2 изменяется в пределах 1 м £ £ z 2 £ 3 м:
на этом участке, где z 2 изменяется в пределах 1 м £ £ z 2 £ 3 м:
S y = 0, - 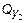 - P + RA = 0,
- P + RA = 0, 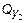 = RA - P (постоянная величина);
= RA - P (постоянная величина);
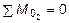 , -
, - 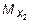 - P × z 2 + RA (z 2 - 1) = 0,
- P × z 2 + RA (z 2 - 1) = 0,
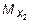 = RA (z 2 - 1) - P × z 2 (уравнение прямой линии).
= RA (z 2 - 1) - P × z 2 (уравнение прямой линии).
Подставив в полученные выражения значения z 2 , соответствующие граничным сечениям участка II, определим величины 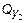 и
и 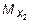 , возникающие в этих сечениях:
, возникающие в этих сечениях:
при z 2 = 1 м 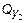 = 40 - 10 = 30 кН,
= 40 - 10 = 30 кН,
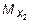 = 40×(1 - 1)-10×1 = -10 кН×м;
= 40×(1 - 1)-10×1 = -10 кН×м;
при z 2 = 3 м 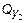 = 30 кН,
= 30 кН, 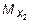 = 40×(3 - 1) - 10×3 = 50 кН×м.
= 40×(3 - 1) - 10×3 = 50 кН×м.
Сделав сечение в пределах участка III, составив и решив уравнения равновесия S y = 0 и  для левой отсеченной части (рис. 5.15), получим аналитические выражения изменения Qy и Mx на участке III, где z 3 изменяется в пределах 3 £ z 3 £ 7 м:
для левой отсеченной части (рис. 5.15), получим аналитические выражения изменения Qy и Mx на участке III, где z 3 изменяется в пределах 3 £ z 3 £ 7 м:
S y = 0, - 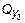 - P + RA - q ×(z 3 - 3) = 0,
- P + RA - q ×(z 3 - 3) = 0,
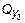 = RA - P - q ×(z 3 - 3) -уравнение прямой;
= RA - P - q ×(z 3 - 3) -уравнение прямой;
 ,
, 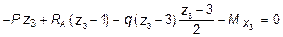 ,
,
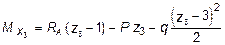 - уравнение параболы.
- уравнение параболы.
 Рис. 5.15
Рис. 5.15
|
Теперь найдем 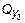 и
и  в граничных сечениях С и В участка III: при z 3 = 3 м
в граничных сечениях С и В участка III: при z 3 = 3 м 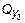 = 40 - 10 -
= 40 - 10 -
- 20×(3- 3) = 30 кН,
 = 40×(3 - 1)-10×3 -
= 40×(3 - 1)-10×3 -  = -50 кН×м;
= -50 кН×м;
при z 3 = 7 м 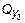 = 40 - 10 - 20×(7 - 3) = -50 кН,
= 40 - 10 - 20×(7 - 3) = -50 кН,
 = 40×(7 - 1) - 10×7 -
= 40×(7 - 1) - 10×7 -  = 10 кН×м.
= 10 кН×м.
Как видно, поперечная сила 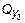 на этом участке принимает в некотором сечении нулевое значение и меняет знак при прохождении через него (рис. 5.13, в). Поэтому в сечении, где
на этом участке принимает в некотором сечении нулевое значение и меняет знак при прохождении через него (рис. 5.13, в). Поэтому в сечении, где  =
=
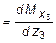 = 0, будет экстремальное значение изгибающего момента. Для его определения найдем величину z 0 , при котором
= 0, будет экстремальное значение изгибающего момента. Для его определения найдем величину z 0 , при котором 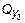 = 0. Приравняв выражение для
= 0. Приравняв выражение для 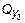 к нулю, получим:
к нулю, получим:
RA - P - q ×(z 0 - 3) = 0,  м.
м.
Подставив найденное значение z 0 = 4,5 м в выражение для  , найдем величину экстремального значения изгибающего момента на этом участке M max = 72,5 кН×м.
, найдем величину экстремального значения изгибающего момента на этом участке M max = 72,5 кН×м.
Для получения аналитических выражений изменения Qy и Mx на участке IV целесообразно начало координат перенести в сечение D и рассматривать равновесие правой отсеченной части, т.к. в этом случае вследствие меньшего количества внешних сил, приложенных к правой части балки, аналитические выражения будут проще по своему виду, а вычисление ординат менее трудоемко.
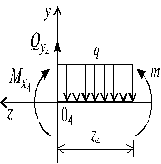 Рис. 5.16
Рис. 5.16
|
Аналитические выражения 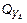 и
и 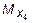 на участке IV (рис. 5.16) (0 £ z 4 £ £ 1 м) получим из следующих уравнений:
на участке IV (рис. 5.16) (0 £ z 4 £ £ 1 м) получим из следующих уравнений:
S y = 0, - 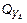 - q × z 4 = 0,
- q × z 4 = 0, 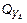 = q × z 4 - (прямая линия);
= q × z 4 - (прямая линия);
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 363; Нарушение авторских прав?; Мы поможем в написании вашей работы!