Тема 2.10. Устойчивость центрально сжатых стержней

Для заметок.

Вопросы для самопроверки.

1. На каком принципе основан расчет на прочность деталей с уче­том сил инерции? В чем этот принцип заключается?

2. На каких допущениях основан расчет деталей на прочность при ударе?

3. В какой последовательности вычисляют динамические напря­жения и перемещения, возникающие в детали при ударе?

4. Чему равен динамический коэффициент при внезапном прило­жении к детали нагрузки?

5. Как определить динамический коэффициент при внезапном приложении к детали нагрузки?

6. Как определить динамический коэффициент при ударе по упру­гой системе горизонтально движущимся телом?

7. Как уменьшить динамические нагрузки и напряжения, возни­кающие в элементах конструкций при ударах?

2.10.1. понятие об устойчивости формы равновесия упругих тел.

2.10.2. Критическая сила. Коэффициент запаса устойчивости. Формула Эйлера.

2.10.3. Критическое напряжение. Пределы применимости формулы Эйлера. Формула Ясинского.

2.10.1.В теме 2.2. показано, что прочность стержня при сжатии не нарушается, если возникающее в его поперечных сечениях напряжение не превышает предельного значения для мате­риала, из которого изготовлен стержень. Длину стержня при его расчете на прочность не учитывали. Однако, как по­казывает опыт, потеря работоспособности стержня может произойти при напряжениях, значительно меньших преде­ла текучести или прочности, вследствие того что стержень не сохранит свою начальную прямолинейную форму. Если взять, например, линейку и приложить к ней сжимающие силы, то при некотором их значении линейка начнет изгибаться, т. е. потеряет свою начальную прямоли­нейную форму. Напряжения сжатия в попереч­ных сечениях линейки при этом значительно ниже предела текучести. При дальнейшем даже незначительном увеличе­нии силы линейка будет продолжать изгибаться до тех пор, пока не сломается. Очевидно, для надежной работы конст­рукции, включающей длинные тонкие (гибкие) стержни, не­обходимо, чтобы они устойчиво сохраняли форму равновесия.

Из курса теоретической механики известны три вида равновесия тел: устойчивое, неустойчивое и безразличное. Равновесие тела называют устойчивым, если отклоненное от положения равновесия тело после устранения причины, вызывающей это отклонение, возвращается в исходное по­ложение.Если откло­нение тела после устранения причины, его вызвавшей, про­должает увеличиваться, то равновесие неустойчивое. Например, шар, лежащий на выпуклой сферической по­верхности.

Аналогично можно выделить три вида упругого равнове­сия длинного тонкого (гибкого) стержня, нагруженного сжимающей силой. Пока сила меньше определенного для данного стержня значения, стержень устойчиво сохраняет прямолинейную форму равновесия (рис. 2.10.1. А). При при­ложении к стержню поперечной нагрузки он изогнется, а после ее снятия вы­прямится. При постепенном увеличении силы, сжимающей стержень, требуется все меньшая нагрузка для его изгиба, и после ее снятия стержень все медлен­нее, как бы «неохотнее», возвращается к первоначальной прямолинейной форме. Наконец, при некотором значении про­дольной сжимающей силы стержень не вы­прямится, а останется изогнутым — пря­молинейная форма равновесия стержня перестала быть устойчивой (рис. 2.10.1. Б).

При этой нагрузке стержень находится в безразличном равновесии — можно немного изменить про­гиб и стержень сохранит приданную ему форму. Если на­грузку немного уменьшить, стержень выпрямится, если да­же незначительно увеличить — стержень будет изгибаться до тех пор, пока не приобретет устойчивую криволинейную форму равновесия или не разрушится. Можно на простом опыте с линейкой заметить, что после потери устойчивости прямолинейной формы равновесия даже не­большим приращениям сжимающей силы соответствуют большие приращения прогиба стержня.

Изгиб стержня, связанный с потерей устойчивости пря­молинейной формы равновесия, называют продольным.

2.10.2. Наибольшее значение центрально приложенной сжимающей силы , при котором стержень еще устойчиво сохраняет прямолинейную форму равновесия, называют критическим.

Потеря устойчивости прямолинейной формы равновесия нарушает нормальную работу конструкции, поэтому крити­ческую силу рассматривают как предельную. Потеря устой­чивости формы упругого равновесия возможна не только для гибких стержней, нагруженных сжимающей силой, но и для таких элементов конструкций, как тонкостенные обо­лочки, пластины и др.

Условие устойчивости прямолинейной формы упругого равновесия стержня имеет вид

,

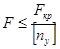где F — действующая на стержень сжимающая сила; — допускаемый коэффициент запаса устойчивости.

Формула для определения критической силы сжатых стержней получена академиком Петер­бургской академии наук Л. Эйлером (1744 г.). Пусть стержень с шарнирно закреплёнными концами нагружен центрально приложенной сжимающей силой (рис. 2.10.1.), тогда значение критической силы вычисляется по формуле

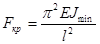, (2.10.1.)

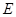где - длина стержня, - модуль Юнга, - наименьший осевой момент инерции сечения (продольный изгиб стержня при потере устойчивости происходит в плоскости наименьшей жесткости, т. е. все сечения стержня поворачиваются относительно оси с наи­меньшим моментом инерции сечения).

Для стержней с другими видами закрепления их концов формулы отличаются от (2.10.1.) только числовым множителем в знаменателе. В общем случае при любом закреплении концов стержня формулу для критической силы, называемую формулой Эйлера, записывают в виде

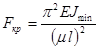, (2.10.2.)

где 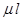— приведенная длина стержня; — коэффициент приведения длины.

Выражение «приведенная дли­на» означает, что в формуле Эйле­ра с помощью коэффициента все случаи закрепления концов стержня можно привести к основ­ному, шарнирному закреплению, для которого и была выведена формула. На рисунке 2.10.2. показа­ны наиболее часто встречающиеся на практике случаи закрепле­ния концов стержня и соответст­вующие им значения коэффици­ента

Из формулы Эйлера (2.10.2.) следует, что нельзя увеличить критическую силу, применив для стержня более прочную сталь, так как в формулу входит единственная характерис­тика материала — модуль упругости 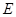, значение которого для всех марок сталей примерно одинаково.

2.10.3. Критическим называют напряжение, возникающее в попе­речном сечении стержня, нагруженного критической силой:

.

Подставив выражение для критической силы (2.10.2.), по­лучим

.

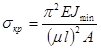Объединим две характеристики сечения и в одну, называемую минимальным радиусом инерции сечения:

,

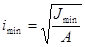тогда

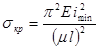. (2.10.3.)

Отношение приведенной длины стержня к минимально­му радиусу инерции называют гибкостью стержня

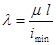. (2.10.4.)

С учетом (2.10.4.) формула (2.10.3.) для критического на­пряжения примет вид

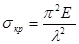
Вывод формулы Эйлера основан на интегрировании диф­ференциального уравнения упругой линии, следовательно, она справедлива только для случая, когда критические на­пряжения в стержне не превышают предела пропорциональ­ности материала, т. е. в пределах применимости закона Гука. Следовательно, формула Эйлера применима при условии

,

или

.

Наименьшую гибкость стержня, при которой еще приме­нима формула Эйлера, называют предельной:

.

Условие применимости формулы Эйлера можно записать в виде

.

т. е. при гибкости стержня меньше предельной формула Эйлера для определения критической силы неприменима. Заметим, что значение предельной гиб­кости зависит только от материала стержня. Например, для стали СтЗ с характеристиками 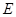= 2 • 10¹¹ Па, 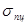= 200 МПа .

Если гибкость стержня меньше предельной и формула Эйлера неприменима, расчет стержня на устойчивость вы­полняют по эмпирической формуле Ясинского

,

где и — коэффициенты, зависящие от материала (напри­мер, для стали СтЗ = 310 МПа, = 1,14 МПа).

При некотором значении гибкости стержня 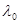критиче­ское напряжение, определяемое по формуле Ясинского, ста­новится равным предельному напряжению при сжатии. Стержни, имеющие гибкость 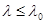, называют стержнями малой гиб­кости и рассчитывают на прочность при сжатии. Стержни с 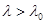называют стержнями средней гибкости и рассчиты­вают на устойчивость по формуле Ясинского. Стержни боль­шой гибкости, имеющие , рассчитывают на устой­чивость по формуле Эйлера.

Условие устойчивости, как и условие прочности, позволяет выполнять три вида расчетов: проверочный, про­ектный и определение допускаемой нагрузки.

Анализ формул Эйлера и Ясинского показывает, что кри­тические значения силы и напряжения зависят от минимального момента инерции поперечного сечения стержня. В связи с этим для гибких стержней, нагруженных сжимающей силой, рациональными являются сечения, имеющие одинаковые моменты инерции относительно любых центральных осей. Наиболее рациональны кольцевые и тонкостенные коробчатые сечения.

Дата добавления: 2015-06-30