Числовые и степенные ряды

Выражение называется числовым рядом и обозначается .

Числа 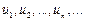называются членами ряда, n -й член ряда называется также общим членом ряда.

Сумма n первых членов ряда называется n -й частичной суммой ряда

.

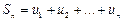Если существует конечный предел , то его называют суммой ряда и говорят, что ряд сходится. Иначе ряд называют расходящимся и не имеющим суммы.

Необходимый признак сходимости ряда. Если ряд сходится, то предел его общего члена равен нулю: 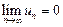(обратное утверждение не выполняется).

Отметим, если , то ряд расходится.

Исследование числовых рядов на сходимость осуществляется с помощью достаточных признаков сходимости.

1. Признак сравнения. Пусть даны ряды и с положительными членами и 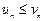(n =1,2,…). Тогда из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

Сравнение исследуемых рядов обычно проводится с рядами:

(геометрическая прогрессия, сходящаяся при 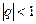и расходящаяся при ),

(расходящийся гармонический ряд),

(обобщенный гармонический ряд, сходящийся при p > 1 и расходящийся при ).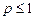

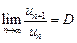Признак Даламбера. Пусть дан ряд с положительными членами и существует предел . Тогда при ряд сходится, а при расходится. При 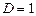признак не отвечает на вопрос о сходимости.

Радикальный признак Коши. Пусть дан ряд с положительными членами и существует предел . Тогда при ряд сходится, а при 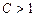расходится. При 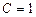признак не отвечает на вопрос о сходимости.

Интегральный признак Коши. Пусть дан ряд 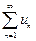, члены которого являются значениями некоторой функции при целых значениях аргумента х, положительной, непрерывной и убывающей в интервале (1; +¥):

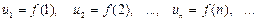
Тогда ряд сходится, если сходится несобственный интеграл , и расходится, если этот интеграл расходится.

Несобственный интеграл вычисляется следующим образом:

.

Интегральный признак является универсальным, т.е. применим тогда, когда не применим ни признак Даламбера, ни радикальный признак Коши, но и наиболее трудоемки, так как доказательство сходимости интегралов часто технически сложно.

Ряд называется знакопеременным, если среди его членов имеются как положительные так и отрицательные.

В знакочередующемся ряде члены поочередно то положительны, то отрицательны, т.е.

.

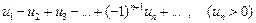Теорема Лейбница. Знакочередующийся ряд 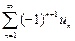сходится, если абсолютные величины его членов монотонно убывают, т.е. 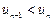, и общий член ряда стремится к нулю: .

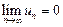Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов .

Если ряд, составленный из абсолютных величин его членов расходится, то данный знакопеременный ряд сходится условно.

П р и м е р ы исследований на сходимость числовых рядов.

1. .

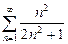Заметим, что .

Необходимое условие сходимости не выполняется. Ряд расходится.

2. .

Сравниваем с гармоническим рядом .

Так как для всех n и ряд расходится, то по признаку сравнения исходный ряд расходится.

3. .

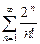Применим признак Даламбера:

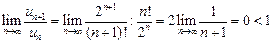. Ряд сходится.

4. .

Применим радикальный признак Коши:

. Ряд сходится.

5. .

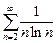Применим интегральный признак Коши.

Так как f(n) =1/(n ln n), то функцией, принимающей в точках х=n значения f(n), будет функция f(х) =1/(х ln х). Она непрерывна в промежутке и монотонно в нем убывает.

Вычислим интеграл

.

Интеграл расходится. Из его расходимости следует расходимость данного ряда.

6. .

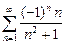Это знакочередующийся ряд. Применим теорему Лейбница.

1) Покажем, что члены ряда монотонно убывают, т.е. выполняется условие . .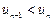

Это неравенство равносильно неравенству 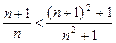или

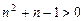.Последнее неравенство справедливо для всех n.

2) Покажем, что 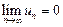. Имеем

.

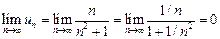Условия теоремы Лейбница выполняются. Данный знакопеременный ряд сходится.

Исследуем сходимость ряда .

Применим интегральный признак Коши

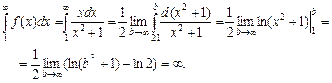
Несобственный интеграл расходится. Ряд, составленный из абсолютных величин, расходится.

Следовательно, знакопеременный ряд сходится условно.

Степенным рядом называется функциональный ряд

,

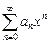где 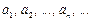– постоянные, называемые коэффициентами ряда. Степенной ряд всегда сходится, по крайней мере при х = 0.

Теорема Абеля. Если степенной ряд сходится при , то он сходится и притом абсолютно для всех значений х, удовлетворяющих неравенству 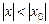. Если ряд расходится при 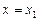, то он расходится при любых х, удовлетворяющих неравенству .

Из теоремы Абеля следует, что существует симметричный интервал 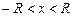, для всех точек которого ряд сходится, а для всех точек вне интервала ряд расходится. Этот интервал называется интервалом сходимости, число R называется радиусом сходимости степенного ряда.

Радиус сходимости можно вычислить по одной их формул:

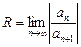или .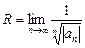

Точки и также могут быть точками сходимости степенного ряда, поэтому в этих точках проводят дополнительное исследование.

П р и м е р. Найти интервал сходимости степенного ряда . Исследовать сходимость ряда на концах интервала.

Воспользуемся признаком Даламбера . , . .

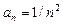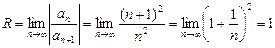Следовательно, ряд сходится в интервале (–1;1). Проверим сходимость в граничных точках х = – 1 и х = 1.

При х = – 1 имеем знакочередующийся ряд 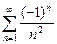, который сходится по теореме Лейбница.

При х = 1 имеем ряд , сходимость которого устанавливается с помощью интегрального признака Коши.

Таким образом, область сходимости [–1;1].

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. М., Наука, Физматлит, 2000.

Краснов М.Л., Киселев А.И., Макаренко Г.И. Шикин Е.В., Заляпин В.И. Вся высшая математика: Учебник. Т.1 – Т.6. Издательство УРСС, 2002.

Кудрявцев Л.Д. Краткий курс математического анализа. т. 1, 2. Альфа, 1998 (Физматлит, 2005).

Шипачев В.С. Высшая математика. М. Высш. школа. 2002.

Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1.: М. Высш. школа. 1996.

Учебное издание

учебное Пособие

ДЛЯ выполнения КОНТРОЛЬНОЙ РАБОТЫ № 2

ПО МАТЕМАТИКЕ

Для студентов всех направлений

квалификация (степень) «бакалавр», «специалист»

заочной формы обучения

Составители: Сайко Дмитрий Сергеевич

Чернышов Александр Данилович

Минаева Надежда Витальевна

Кузнецов Сергей Фёдорович

Ковалёва Елена Николаевна

Половинкина Марина Васильевна

Никифорова Ольга Юрьевна

Соболева Елена Александровна

Подписано в печать 01.2014. Формат 60 х 84 1/16.

Усл. печ. л. 1,5. Тираж 150 экз. Заказ.С – 28.

ФГБОУ ВПО «Воронежский государственный университет

инженерных технологий» (ФГБОУ ВПО «вгуит»)

Отдел оперативной полиграфии ФГБОУ ВПО «вгуит»

Адрес университета и отдела оперативной полиграфии:

394036 Воронеж, пр. Революции, 19.

Дата добавления: 2015-06-30