Минимизация методом Квайна

Метод Квайна имеет четко сформулированный алгоритм осуществления отдельных операций и поэтому может быть использован для реализации на ЭВМ [4].

Для проведения минимизации этим методом требуется достаточно много времени ввиду необходимости попарного сравнения друг с другом каждого члена логической функции. При минимизации по методу Квайна предполагается, что исходная функция задана в СДНФ.

Суть метода в следующем.

1 Осуществляется переход от канонической формы записи ФАЛ (СДНФ) к сокращенной на основе формулы склеивания

, (4.1)

где W – одинаковая часть выражения в обеих конъюнкциях формулы,

Х – переменная, которая в разных конъюнкциях имеет противоположные значения.

2 Выполняется переход от сокращенной формы ФАЛ к минимальной с применением формулы поглощения

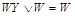, (4.2)

где Y – часть конъюнкции, которая в одной конъюнкции присутствует, а в другой отсутствует.

Рассмотрим упрощение ФАЛ методом Квайна на примере. Пусть ФАЛ задана табличным способом (таблица 4.1).

Запишем СДНФ функции, заданной ТИ. В формуле каждую конъюнкцию пронумеруем соответственно ее порядковому номеру в ТИ. Нумерация нужна для отслеживания попарного перебора всех конъюнкций на предмет применения правила склеивания.

.

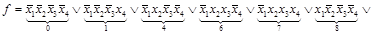
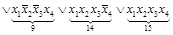На первом этапе, в полученной формуле, сравниваем попарно все конъюнкции (минтермы четвертого ранга) и применяем там, где это возможно, правило склеивания. Склеиванию могут подвергаться только те конъюнкции, которые различаются инверсией лишь одной переменной. Для рассматриваемой функции склеиваются соответственно 0 и 1, 0 и 4, 0 и 8, 1 и 9, 4 и 6, 6 и 7, 6 и 14, 7 и 15, 8 и 9, 14 и 15 конъюнкции. Склеенные минтермы четвертого ранга отмечаются номерами под каждым минтермом третьего ранга с целью отследить, все ли исходные конъюнкции подверглись склеиванию. После первой итерации склеивания получена сокращенная функция из минтермов третьего ранга.

.

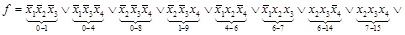
По номерам под минтермами проверяем, все ли исходные минтермы четвертого ранга склеились. Так как в полученной формуле присутствуют номера всех исходных конъюнкций, то это означает, что все они подверглись первичному склеиванию. В том случае, если номер какой-то исходной конъюнкции отсутствует в преобразованной формуле, эта конъюнкция должна быть введена в эту формулу через знак дизъюнкции во избежание искажения результата функции.

Далее, если это возможно, к минтермам функции, имеющим одинаковый ранг, снова применяется правило склеивания. В полученной функции склеиванию подвергаются соответственно минтермы третьего ранга 0–1 и 8–9, 0–8 и 1–9, 6–7 и 14–15, 6–14 и 7–15. В результате образуются минтермы второго ранга. При этом минтермы 0–4 и 4–6 не подвергаются склеиванию с другими минтермами. Поэтому они присутствуют в сокращенной форме функции.

.

Анализируя полученную формулу, можно заметить, что минтермы и в формуле повторяются и, согласно закону повторения, повторяющиеся члены могут быть удалены из формулы. Если больше склеить ничего не удается, то на этом первый этап упрощения заканчивается.

На втором этапе составляется так называемая импликантная таблица или таблица поглощений (перекрытий). Данная таблица позволяет упростить применение правила поглощения и одновременно отследить, все ли исходные конъюнкции (импликанты) учитываются в упрощенном выражении.

В импликантную таблицу (таблица 4.2) входят все исходные конъюнкции (в столбцах) и все конъюнкции, подвергшиеся склеиванию на последнем этапе (в строках), включая те, которые не склеились (если они имеются). В таблице на пересечении строки и столбца, к минтермам которых может быть применено правило поглощения, ставится отметка.

После проставления всех отметок выбираются ядра (ядро) упрощенной функции.

Ядро функции – это та сокращенная импликанта, которая единолично перекрывает какие-либо столбцы таблицы (т.е. в этих столбцах стоит только одна отметка).

Упрощенная функция может иметь несколько ядер или не иметь их вообще. Если функция имеет ядро(а), то оно(и) должно(ы) обязательно присутствовать в минимальной формуле. Если функция не имеет ядра, то условно за ядро принимается та сокращенная импликанта, которая является наиболее простой и одновременно перекрывает как можно больше столбцов исходных импликант функции.

Рассматриваемая функция имеет два ядра. Это обе минтермы второго ранга и . Все отметки ядер (как первого, так и второго) сносятся в строку перекрытий импликантной таблицы. После этого выполняется проверка: все ли клетки строки перекрытий заполнены. Если заполнены все клетки, то результатом упрощения исходной функции будет дизъюнкция ядер. В противном случае ищутся дополнения к ядрам для заполнения всей строки перекрытий. Для упрощаемой функции осталась одна незаполненная клетка, поэтому необходимо искать дополнение.

Дополнение – это та сокращенная импликанта, которая позволяет оптимальным образом заполнить оставшиеся клетки строки перекрытий. Дополнения необходимо выбирать таким образом, чтобы они были как можно проще (имели меньшее количество переменных) и одновременно перекрывали как можно больше незаполненных клеток строки перекрытий. При этом формула упрощенной функции будет состоять из ядер(а) и дополнений(я).

Так как дополнений может быть несколько, то и формула упрощенной функции может быть различна. Формула упрощенной функции может различаться только дополнениями.

В рассматриваемом варианте функции возможны два варианта дополнения: либо 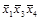, либо , так как отметки от той и другой импликанты позволяют перекрыть незаполненную клетку.

Т а б л и ц а 4.2 – Таблица перекрытий

№ п/п	Упрощенные импликанты	Исходные импликанты
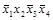
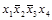
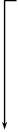		V	V				V	V
		V		V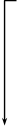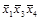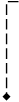
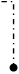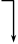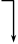				V	V
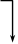					V	V		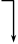	V	V
Строка перекрытий	V	V	V	V	V	V	V	V	V
Примечания: 1 Овалом выделены те упрощенные импликанты, которые составляют ядро функции. 2 Сплошными линиями показаны направления переноса отметок поглощения в строку перекрытий от ядер функции. 3 Штриховой и штрихпунктирной линиями соответственно показаны направления переноса отметок перекрытия от первого и второго вариантов дополнений функции. 4 Отметки первого ядра показаны в таблице жирным и наклонным шрифтом, отметки второго ядра показаны жирным шрифтом, а отметки дополнений – обычным шрифтом.

За конечный вариант упрощенной функции принимается тот, в котором меньше всего дополнений и они минимальны по количеству вхождений переменных или по количеству инверсий переменных. В данном случае более оптимальным по количеству инверсий переменных является дополнение .

Таким образом, получаем упрощенный методом Квайна вариант функции .

Метод Квайна обладает одним существенным неудобством, которое связано с необходимостью полного попарного сравнения членов СДНФ. При этом с ростом числа членов растет и число сравнений в факториальной зависимости. В 1956 г. Мак-Класки предложил модернизировать метод Квайна, что позволило уменьшить число сравнений. Усовершенствованный метод получил название метода минимизации Квайна–Мак-Класки. Рассмотрим идею данного метода более детально.

4.2.4 Минимизация методом Квайна–Мак-Класки

Суть метода в следующем [1]. Члены СДНФ записываются в виде их двоичных номеров. Все номера разбиваются на группы по числу единиц в них. При этом в i- ю группу входят все номера, которые имеют в своем двоичном коде количество единиц равное i. Затем выполняется попарное сравнение членов соседних по номеру групп (т.е. реализуется закон склеивания по отношению к кодовым комбинациям), так как только члены этих групп отличаются лишь в одном разряде. При образовании членов с рангом (числом единиц) выше нулевого в разряды, соответствующие исключенным переменным, пишется знак тире (прочерк). В остальном методика не отличается от метода Квайна.

Рассмотрим тот же пример, что и для метода Квайна. Имеем функцию

.

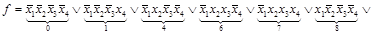
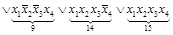Перепишем данную функцию, подставив вместо ее инверсных аргументов «0», а вместо неинверсных – «1» и получим

.

Разобьем номера функции на группы по числу единиц (таблица 4.3).

После разбиения на группы выполняется сравнение соседних групп. При сравнении отыскиваются те пары кодов, которые отличаются одним разря- дом на соответствующих позициях. Тот разряд, которым кодовые комбинации различаются, заменяется прочерком, а полученная комбинация записывается в ту из сравниваемых групп, которая имела меньший номер (таблица 4.4). После первого сравнения полученные члены разложения первого ранга также сравниваются между собой. Таких сравнений может быть как меньше, так и больше двух. Это зависит от величины кодовой комбинации и возможностей склеивания комбинаций. В сравнении участвуют только те комбинации, в которых прочерки находятся на одинаковых позициях. Если какие-либо комбинации не подверглись склеиванию, то их вес не уменьшается, и они остаются на своем месте в группе.

Далее, аналогично таблице 4.2, строится таблица поглощений (таблица 4.5), в которую входят все исходные коды (в столбцах) и все коды после последнего склеивания (в строках).

Как видим, получена таблица поглощений, похожая на ту, которая была образована в методе Квайна. Отличие таблицы состоит лишь в том, что вместо импликант, в ней записаны кодовые комбинации. Запишем упрощенное выражение функции аналогично тому, как это было сделано в методе Квайна: .

Заменим символы нуля и единицы соответствующими им аргументами и получим окончательное выражение упрощенной функции методом Квайна–Мак-Класки – .

Дата добавления: 2015-07-02