Ошибки выборки и методы вычисления средней и предельной ошибки для разных видов выборки

Для того, чтобы иметь основания распространить результаты выборочного наблюдения на генеральную совокупность, необходимо знать, насколько хорошо выборочная совокупность представляет генеральную. То есть, или репрезентативная выборка.

Выборка, как уже отмечалось, считается репрезентативной, если обобщающие показатели выборочной и генеральной совокупности достаточно близки.

Обычно складывают такие показатели выборочной и генеральной совокупности:

– среднюю величину того или другого признака у единиц совокупности (ср. зарплата, ср. доход, ср. урожайность);

– часть единиц, которые имеют тот или другой признак, то есть удельный вес определенных единиц в совокупности (часть лиц с высшим образованием, часть женщин в общей численности работников и так далее).

Разница между этими показателями выборочной и генеральной совокупности и называется ошибкой репрезентативности, то есть:

, ошибка репрезентативности средней

, ошибка репрезентативности для части.

Выборочное среднее и часть является переменными величинами, поскольку они могут приобретать разные значения в зависимости от того, какие единицы генеральной совокупности попали в выборку.

То есть из одной и той же генеральной совокупности можно сделать ряд выборок равного объема. При этом каждая выборка будет иметь свою ошибку репрезентативности для средней и для остатка.

Поэтому из всех возможных ошибок репрезентативности определяется средняя ошибка выборки, которая обозначается буквой µ. Ее еще называют стандартная ошибка.

Прежде чем записать формулы, с помощью которых определяются средние ошибки выборки, рассмотрим, от чего зависит величина этих ошибок.

Очевидно, что чем больше единицы отбираются из генеральной совокупности, тем ближе выборочные показатели (средняя и часть) приближаются к генеральным.

А если численность выборки (n) достигнет численности генеральной совокупности (N), то есть когда выборочное наблюдение превратится в сплошное, то вообще никаких расхождений между выборочными и генеральными показателями не будет, а ошибка выборки будет равняться нулю. Следовательно:

1) ошибка выборки зависит от объема (численности) выборки - обратно пропорциональная численности выборки;

2) ошибка выборки зависит от уровня колебаний (варьирование) значений признака в генеральной совокупности, прямо пропорциональная колебанию значений признака в генеральной совокупности;

3) от способа отбора единиц из генеральной совокупности.

Уровень колебаний значений признака в совокупности определяется, как известно, показателями вариации. Основной из них является дисперсия 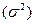и СКВ .

Из группы теорем Закона больших чисел выплывает:

– при собственно-случайном отборе, организованном по схеме повторной выборки, между ошибкой выборки µ, дисперсией 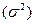и численностью выборки (n) существует такая зависимость:

.

То есть средняя ошибка выборки есть СКО выборочной средней от генеральной. Она равняется корню квадратному из отношения дисперсии признака в генеральной совокупности к числу единиц выборочной совокупности.

Но поскольку практически дисперсия признака в генеральной совокупности неизвестна, то в приведенной формуле используют дисперсию или СКВ выборочной совокупности.

Это обосновано тем, что при соблюдении принципа случайности отбора единиц из генеральной совокупности дисперсия достаточной по объему выборки стремится отобразить дисперсию в генеральной совокупности. При этом она меньше генеральная на величину 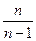() (если n достаточно большое, то это отношение близко к единице).

В случае малой выборки, то есть когда численность ее менее 30 единиц, в знаменателе формулы вместо (n) берется (n - 1), то есть

.

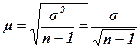Если выборочное наблюдение применяется для определения части какого-либо признака в совокупности, то средняя ошибка выборочной части вычисляется по формуле

,

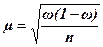где - часть единиц, которые имеют данный признак в выборке;

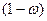– часть единиц, которые не владеют данным признаком;

– количество единиц выборки;

– дисперсия части признака в выборочной совокупности.

При собственно-случайном отборе, организованном по схеме бесповторной выборки, численность единиц генеральной совокупности в процессе отбора сокращается.

Поэтому при бесповторном отборе в приведенной формуле вводится дополнительный множитель

,

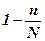где - количество отобранных единиц;

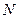– количество единиц генеральной совокупности;

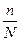– часть отобранных единиц из генеральной совокупности;

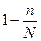– часть неотобранных (что остались) единиц генеральной совокупности.

Тогда средняя ошибка выборочного среднего при бесповторном отборе равняется:

,

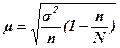а средняя ошибка части

.

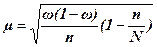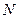Поскольку всегда меньше то множитель (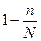) всегда меньше единица. Поэтому величина средней ошибки выборки при бесповторном отборе меньше, чем при повторном, поскольку подкоренное значение формулы множиться на число, меньшее единицы.

При сравнительно небольшой части отобранных единиц, данный множитель будет близок к единице и им можно пренебречь.

На практике часто при определении средней ошибки выборки используют формулы без этого множителя, хотя выборка и организована как бесповторная.

Величина ошибки выборки при этом несколько увеличивается.

Приведенные формулы дают возможность определить величину среднего отклонения выборочного среднего от генерального, или выборочной части признака от генеральной части.

Вместе с тем при решении практических задач одной только средней ошибки выборки недостаточно.

Это связано с тем, что при определении ошибки конкретной выборки фактическая ошибка может быть больше или меньше средней µ. Поэтому на практике пользуются обычно не средней, а предельной ошибкой выборки, то есть пределами, за которые не выйдет фактической ошибки выборки. Она позволяет установить, в каких пределах находится величина генеральной средней.

Предельная ошибка выборки 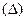кроме всего прочего, зависит еще и от того, с какой вероятностью она гарантируется.

На величину вероятностей указывает коэффициент доверия который определяется на основе теорем П.Л. Чебышева и А.М. Ляпунова и интеграла Лапласа:

.

Эти теоремы определяют вероятность того, что предельная ошибка выборки 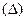не превысит 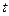-кратную (взятую 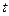раз) среднюю ошибку выборки (().

Т.о., 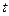свидетельствует о вероятности расхождения 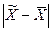то есть о вероятности того, на какую величину генеральная средняя будет отличаться от выборочной средней.

Да, с вероятностью 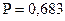можно гарантировать, что разница между выборочной и генеральной средней не превысит величину однократной средней ошибки выборки.

С вероятностью 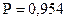можно гарантировать, что размер предельной ошибки не превысит двукратную среднюю ошибку (при 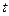=2).

С вероятностью 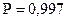- не превысит 3-кратную среднюю ошибку (при 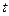=3).

Т.о., величину предельной ошибки выборки вычисляют с некоторой вероятностью (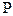), какой отвечает 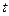-кратное значение µ.

Величина вероятностей для разных значений коэффициента (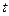) приводится в специально рассчитанных таблицах, которые приводятся в курсе математической статистики.

Рекомендуется запомнить такие значения соответствующих друг другу 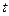и .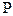

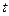
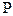
	0,683
	0,954
	0,997
	0,999

Т.о., предельная ошибка выборки зависит от трех факторов:

– объему выборки ;

– уровня колебания значений признака ;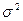

– необходимой гарантированной вероятностей коэффициента доверия .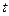

С введением коэффициента кратности ошибки формула предельной ошибки имеет вид

.

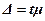Подставив в эту формулу вместо µ ее аналитическое выражение, одержимо общие формулы предельной ошибки.

1 При повторном собственно-случайном отборе:

– для средней величины признака ;

– для части .

2 При бесповторном собственно-случайном и механическом:

– для среднего ;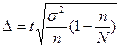

– для части .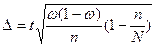

3 При типичном отборе дисперсией признака средняя из внутригрупповых дисперсий:

,

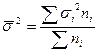где 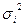- выборочная дисперсия в i- и типичной группе, она определяется за формулой: ;

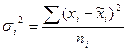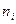– число единиц в i- и типичной группе.

Для остатка средняя из внутригрупповых дисперсий определяется

.

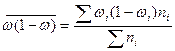Тогда предельная ошибка выборочной средней при типичном повторном отборе будет равняться

;

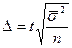части .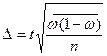

4 При типичном бесповторном отборе

для средней ;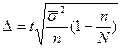

для части .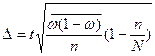

Предельная ошибка выборки при типичном отборе всегда меньше ошибка при собственно-случайном отборе, поскольку групповая дисперсия меньше общей дисперсии.

5 При серийном (гнездовом) отборе каждая из отобранных серий рассматривается как единица совокупности.

Мерой колебания является межсерийная выборочная дисперсия (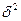), то есть средний квадрат отклонений серийных выборочных средних от общей выборочной средней

,

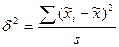где 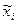- средняя из каждой серии;

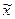– общая выборочная средняя;

– число отобранных серий.

Предельная ошибка средней при серийном повторном отборе ;

ошибка части .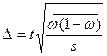

6 При серийном бесповторном отборе

для средней ;

для части ,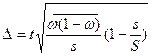

где 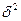- межсерийная дисперсия;

– число отобранных серий (в выборочной совокупности);

– число серий в генеральной совокупности.

Дата добавления: 2015-07-02