VII. Разложение непериодической функции

VI. Нахождение сумм числовых рядов.

Функция называется кусочно-монотонной на отрезке 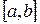, если этот отрезок можно разбить на конечное число отрезков:

, внутри каждого из которых функция либо строго монотонна (только возрастает или только убывает) либо постоянна. (см. второе условие Дирихле).

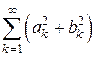Пусть периодическая функция ограничена и кусочно-монотонна на отрезке , тогда в случае, если интегрируема, ряд сходится и верно равенство 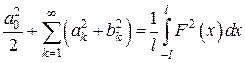, где

(или , учитывая периодичность ).

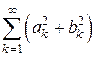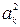Это равенство называется равенством Парсеваля-Ляпунова. С его помощью находится сумма ряда , где и - коэффициенты ряда Фурье.

Рассмотрим непериодическую функцию , заданную на всей числовой прямой. Ясно, что нельзя найти такой тригонометрический ряд, сумма которого во всех точках равнялась бы этой функции (так как каждый сходящийся тригонометрический ряд имеет своей суммой периодическую функцию).

Известно, что ряд Фурье для периодической функции совпадает с рядом Фурье для функции, полученной периодическим продолжением функции 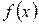с отрезка длины 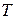, на котором она задана, на всю числовую ось .

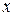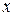Пусть непериодическая функция задана на всей оси и удовлетворяет условиям Дирихле на конечном отрезке 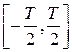. Следовательно, на этом отрезке она может быть разложена в ряд Фурье.

,

, где .

Таким образом:

,

так как , следовательно .

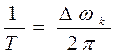Тогда .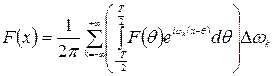

Устремим к бесконечности , тогда и сумма может рассматриваться как интегральная сумма для функции .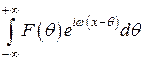

Так как , то преобразуется в непрерывный аргумент , :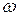

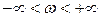, причем переставлять порядок интегрирования нельзя.

Полученное равенство называется интегральной формулой Фурье, правая часть - интегралом Фурье в комплексной форме.

Функция может быть представлена в виде интеграла Фурье если выполнены условия интегральной теоремы Фурье:

1) задана на всей оси ;

2) на любом конечном отрезке оси удовлетворяет условиям Дирихле;

3) абсолютно интегрируема на всей оси , то есть

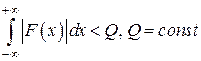, то есть 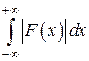сходится.

При этом

a) интеграл Фурье равен во всех точках непрерывности функции;

b) в точках разрыва интеграл Фурье равен .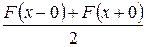

Итак, интеграл Фурье в комплексной форме имеет вид .

Это можно записать иначе: 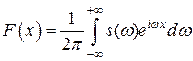- обратное преобразование Фурье, где - прямое преобразование Фурье.

Преобразования, определяемые этими формулами, называются интегральными преобразованиями Фурье (или формулами обращения Фурье), также называется волновым числом, но здесь оно принимает все значения от 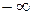до и спектр волновых чисел называется непрерывным спектром.

В то время как разложение в ряд Фурье дает представление периодической функции в виде суммы гармонических колебаний с частотами 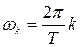, интеграл Фурье представляет функцию как бы в виде суммы бесконечно большого числа колебаний с непрерывно изменяющейся частотой . Говорят, что интеграл Фурье дает разложение функции в непрерывный спектр.

Если задана функция , то посредством обратного преобразования Фурье получают .

Дата добавления: 2015-07-02