Общие свойства числовых рядов

1. (Критерий сходимости Коши) Для того, чтобы числовой ряд 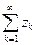сходился, необходимо и достаточно, чтобы для всякого положительного ε можно было указать натуральное n _ε такое,что при всех натуральных n > n _ε и любых натуральных р справедливо неравенство .

► Сходимость числового ряда означает сходимость последовательности {S _n} его частичных сумм. Напомним формулировку критерия Коши сходимости последовательности: для того, чтобы последовательность {S _n} сходилась, необходимо и достаточно, чтобы

.

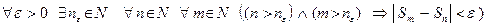Не ограничивая общности можно считать, что m > n, т.е. что m = n + p, где р - некоторое натуральное число. Если n > n _ε, то подавно n + p > n _ε , поэтому написанную выше строчку можно заменить следующей, ей равно- сильной:

.

Заметим: 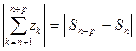; Таким образом, из критерия Коши для последовательности {S _n} вытекает: ряд 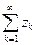сходится тогда и только тогда, когда

,

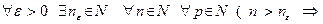
что и требовалось доказать. ◄

Приведем пример применения критерия Коши.

Пример 4, Ряд 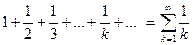называют гармоническим рядом. Покажем, что это расходящийся ряд. Пусть n - некоторое натуральное число; а p = n +2. Рассмотрим В этой сумме n +2 слагаемых, причем - наименьшее из них; поэтому Здесь n - любое натуральное число. Зададим ε, удовлетворяющее неравенствам 0 < ε < ½. Тогда при всяком натуральном n и p = n +2 будет выполнено , а это означает, что для такого ε нельзя указать n _ε, которое удовлетвори- ло бы требованию критерия сходимости Коши. Значит, ряд расходится. ◄

2. (Необходимое условие сходимости) Если ряд 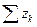.сходится, то его общий член стремится к нулю: z _k → 0_.

► Пусть S _n = 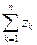. Обозначим сумму ряда через S: S _n → S. При всяком n ≥2, очевидно, z _n = S _n - S _{n -1}. Перейдем в этом равенстве к пределу; так как последовательности 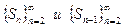имеют один и тот же предел S, получим: z _n → 0. ◄

Замечание. Обратное утверждение (если z _k → 0, то 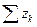сходится) неверно. Действительно, для гармонического ряда имеем z _k → 0, однако ряд расходится. Можно указать еще и на ряд 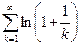, рассмотренный выше (см. пример 2): его общий член,очевидно, стремится к нулю, но ряд расходится.

3. (Достаточное условие расходимости) Если общий член ряда не стремится к нулю, то ряд расходится.

► Действительно, если общий член ряда не стремится к нулю, ряд не может оказаться сходящимся, так как общий член сходящегося ряда обязательно стремится к нулю. ◄

Пример 5. Выше (см. пример 1) мы показали, что ряд сходится, если |q| < 1 и расходится, если |q| > 1. Рассмотрим случай |q| = 1. Имеем: 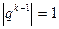при всяком натуральном k, поэтому последовательность заведомо не стремится к нулю; значит. при любом комплексном q, |q| = 1, рассматриваемый ряд расходится.

4. (Умножение числа на ряд) Пусть заданы ряд 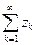и некоторое отличное от нуля число λ, вообще говоря, комплексное. Произведением числа λ на ряд 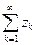называют ряд 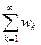, где w_k = λz_k. Справаедливы утверждения: 1) ряды 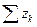и либо оба сходятся, либо оба расходятся; 2) если 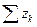= S, то = λ S.

► Пусть n - некоторое натуральное число. Обозначим: . Очевидно, 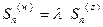.Отсюда и из теоремы об арифметических действиях со сходящимися последовательностями ([3], п. 3.5) вытекает: 1) последовательности частичных сумм либо обе сходятся, либо обе расходятся; 2) если ◄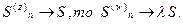

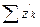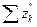5. (Сложение рядав) Ряд называют суммой рядов и . Справедливы утверждения: 1) пусть ряды сходятся, причем ; тогда сходится и , причем = ; 2) если один из рядов сходится, а другой расходится, то ряд расходится.

► Обозначим: 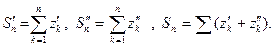Очевидно, 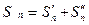. Из теоремы об арифметических действиях со сходящимися последовательностями следует: 1) если последовательности частичных сумм 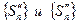сходятся, 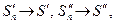то сходится и их сумма - последовательность , причем S_n → →S’+S”; 2) если одна из последовательностей 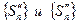сходится, а другая расходится, то не может быть сходящейся последовательностью, значит, ряд расходится. ◄

Замечание. Если оба ряда расходятся, то их сумма, т.е. ряд может оказаться как сходящимся, так и расходящимся рядом. На- пример, положим Тогда ряды расходятся (см. пример 4), а ряд сходится, так как каждый его член равен нулю.

6. Пусть задан ряд 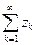, а m - некоторое натуральное число. Ряд , где w_l = = z_m+l , т.е. ряд z_m+1+z_m+2+ …+ z_m+l + … = , называют остатком ряда 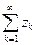. Справедливо утверждение: ряд 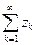и его остаток либо оба сходятся, либо оба расходятся.

► Очевидно, при любом натуральном p т.е. 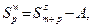где А = = . Ввиду такой связи между последовательностями частичных сумм очевидно, что если сходится одна из них, то сходится и другая; если одна из них расходится, то другая не может быть сходящейся. ◄

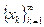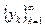7. Пусть и - последовательности вещественных чисел. Обозначим: z_{k =} x_k + i y_k, S_n=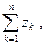 . Если ряды 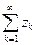, сходятся, то их суммы обозначаем через S, 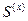и соответственно. Справедливы утверждения: 1 ) ряд 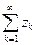сходится тогда и только тогда, когда сходятся оба ряда ; 2 ) если 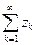сходится, то S = 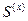+ i .

► Заметим: S_n = S + i S . Утверждения 1 ) и 2 ) вытекают непосредственно из свойств последовательностей комплексных чисел. ◄

3º. Признаки сходимости рядов с неотрицательными членами.

Ряды находят разнообразные применения в прикладной математике. Имея дело с числовым рядом,прежде всего следует выяснить, сходится ли этот ряд. Выяснить это часто удается с помощью свойств, описанных в предыдущем пункте (например, если общий член не стремится к нулю, то ряд расходится). Если указанных средств оказалось недостаточно, обращаются к признакам сходимости и расходимости рядов, наиболее употребительные из которых составляют содержание этого и следующего пунктов.

В этом пункте мы рассматриваем числовые ряды члены которых неотрицательны. Обозначим через S_n частичную сумму такого ряда.: S _n = = .Так как a _k ≥ 0, то S _n ≤ S _{n +1}, т.е. {S _n } - монотонная неубывающая последовательность. Если эта последовательность ограничена сверху, она сходится, в противном случае она стремится к + ∞ ([3], п.3.6). Таким образом, справедлива следующая теорема.

Теорема 1. (Критерий сходимости ряда с неотрицательными членами) Для того, чтобы ряд a _k ≥ 0, сходился, необходимо и достаточно, что- бы последовательность его частичных сумм {S _n } была ограничена сверху.

Пусть f - некоторая функция, определенная на промежутке [ 1, +∞). Обозначим: a _k= f (k), где k , и рассмотрим числовой ряд . Будем называть f производящей функцией для числового ряда . Например, f (x) = 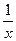является производящей функцией для гармонического ряда 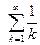, так как при всех натуральных k f (k) = 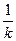. Если производящая функция неотрицательна на [1, +∞), то - ряд с неотрицатеьными членами.

Теорема 2. (Интегральный признак Коши) Пусть производящая функция f числового ряда непрерывна, неотрицательна и монотонно не возрастает на промежутке [1;+∞). Для того, чтобы ряд был сходящимся, необходимо и достаточно, чтобы сходился несобственный интеграл .

► Напомним: по определению = , где F (x) = ; интеграл сходится, если предел конечен, и расходится в противном случае, т.е. если этот предел равен ∞ или не существует ([4], п. 2.1). По условию теоремы f (x) неотрицательна на [1, +∞), поэтому F (x) моно -тонно не убывает [ 1,∞); следовательно, конечен тогда и только тог- да, когда F (x) ограничена на [ 1, +∞) сверху. Отметим еще, что если интег- рал сходится, то F (x) ≤ при всех х 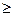1.

Пусть k – натуральное число. Так как f (x) - монотонная невозрастающая функция, то т.е. при Интегрируя последние неравенства, получим: , т.е. . Отсюда: 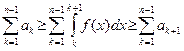, т.е.

N S_n – a_n ≥ 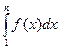≥ S_n – a₁ (2)

Необходимость. Пусть сходится, а S – его сумма: lim S_n = S, где 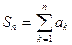. Так как 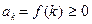, то {S_n} – неубывающая последовательность, и при всяком натуральном n S_n ≤ S_n+1 ≤ S. Из (2) имеем: N 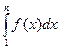≤ S_n –- a_n, и так как S_n ≤ S, то при всех натуральных n справедливо F(n) ≤ S. Отсюда вытекает: функция F ограничена на [1;+∞) cверху числом S; следователь- но (см. выше), интеграл сходится.

Достаточность. Пусть интеграл сходится. Так как F (x) ≤ , то из (2) имеем: при всех натуральных n: ≥ F(n) = 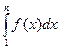≥ S_n – a₁ . Отсюда: N S_n ≤ + а₁, т.е. последовательность {S _n } ограниче- на сверху; значит (см. теорему 1), ряд сходится. ◄

Пример 6. Пусть λ – некоторое вещественное число.Рассмотрим ряд 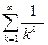. Этот ряд называют обобщенным гармоническим рядом (в частном случае λ =1 получим гармонический ряд, см. пример 4). Если λ ≤ 0, то не стремится к нулю; значит (см. достаточное условие расходимости, 2˚), при λ≤0 обобщенный гармонический ряд расходится. Пусть λ>0. Функция f (x) = = , очевидно, является производящей функцией для ряда 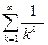; она положительна и убывает на [1;+∞). Таким образом, f (x) удовлетворяет тре- бованиям интегрального признака Коши.

Имеем: при λ≠ 1 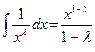, при λ = 1 . Из этих равенств нетрудно вывести, что расходится при 0 < λ ≤ 1 и сходится при λ > 1. По интегральному признаку Коши обобщенный гармонический ряд ведет себя так же.

Итак, ряд 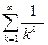расходится при λ ≤ 1 и сходится при λ > 1.

Следующие теоремы дают достаточные условия сходимости или расходимости ряда с неотрицательными членами.

Теорема 3. (Первый признак сравнения) Пусть { a_k } и{ b_k } - две последовательности неотрицательных чисел, причем . Тогда:

1) если 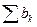сходится, то сходится и ряд ;

2) если ряд расходится, то расходится и ряд .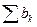

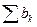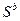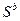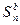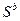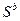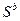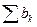► Обозначим: 1) Очевидно, Пусть сходится, а - его сумма: . Так как последовательность частичных сумм монотонно не убывает, то ≤ . Значит, при всех натуральных n ≤ , т.е. последовательность { } ограничена свер- ху числом , и поэтому она сходится. 2) Пусть расходится; тогда Так как , то и → +∞, т.е. ряд расходится.◄

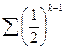Пример 7. Рассмотрим ряд . При всяком натуральном k k! ≥ Следовательно, при всех натуральных k Ряд сходится (пример 1, q = = ½), значит,сходится и рассматриваемый ряд.

Теорема 3. (Второй признак сравнения) Пусть { a_k } – последовательность неотрицательных чисел, а { b_k } – последовательность положительных чисел. Пусть, далее, где q - либо неотрицательное число, либо символ +∞. Тогда:

если 0 < q < + ∞, то ряды и 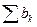ведут себя одинаково – либо

оба сходятся, либо оба расходятся;

2) если q = 0, а ряд 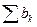сходится, то сходится и ряд ;

3) если q = + ∞, а ряд 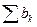расходится, то расходится и ряд .

► 1) Достаточно показать, что из сходимости вытекает сходи –

мость 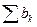, а из расходимости следует расходимость 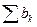. Зададим

ε, 0 < ε < q. Найдется натуральное k_ε, такое, что при всех k > k_ε справедливо неравенство 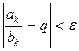, т.е.

(3)

Пусть сходится. Тогда сходится и его остаток . Из неравенств

(см.(3)) и первого признака сравнения вытекает сходимость ряда (заметим, что q – ε > 0). Этот ряд представляет собой остаток ряда , который, следовательно, является сходящимся. Значит (см. свойство 4, п. 2º), 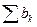сходится.

Пусть расходится. Чтобы вывести отсюда расходимость ряда ,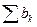

следует воспользоваться неравенствами 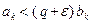, справедливыми при k > > k_ε (см. (3)). Рассуждения аналогичны изложенным выше.

2) Пусть 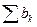сходится. Зададим некоторое ε > 0. Так как 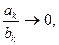най- дется k_ε, такое, что при всех k > k_ε справедливо неравенство , т.е. 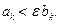Так как 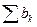сходится, то сходится и его остаток . По свойству 4, п. 2º, сходится ряд 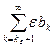. Отсюда и из первого признака сравнения вытекает сходимость ряда , который представляет собой остаток ряда . Значит, сходится.

3. Пусть 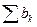расходится. Так как найдется натуральное k₁ та

кое, что при всех k > k₁ справедливо По первому признаку сравнения из 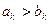вытекает расходимость ряда , который представляет собой остаток ряда . Значит, расходится. ◄

Замечание. Доказанная теорема производит сравнение двух рядов по “ско- рости” убывания их общих членов. Если общие члены рядов и 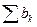являются бесконечно малыми одинакового порядка (, q ≠ 0, +∞), то ряды ведут себя одинаково; в частности, ряды ведут себя одинаково, когда их общие члены эквивалентны (случай q = 1). Если общий член ряда является бесконечно малой более высокого порядка по сравнению с об- щим членом сходящегося ряда 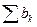(a_k =o (b_k)), то также сходится; если общий член a_k убывает “медленнее“ общего члена расходящегося ряда 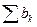, то ряд также расходится.

Чтобы эффективно применять признаки сравнения, нужно располагать набором рядов, относительно которых уже известно, сходятся они или расходятся, и чем больше различных рядов в этом наборе, тем больше шансов най- ти среди них такой, сравнение с которым позволит выяснить, сходится ли интересующий нас ряд. Мы уже можем включить в этот набор различные ря- ды вида , где a и q положительные числа – такой ряд сходится, если 0 < q < 1, и расходится, если q ≥ 1 (cм.примеры 1 и 5). В этот набор можем включить также обобщенный гармонический ряд 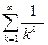при всевозможных вещественных λ (пример 6). Вообще, каждый ряд, сходимость которого исследована, пополняет указанный набор рядов.

На второй признак сравнения опирается метод выделения главной части в иследовании рядов на сходимость. Пусть f (x) есть производящая функция ряда : a_k = f (k). Пусть, далее, С , где С > 0 и λ > 0, - главная часть f (x) при х → +∞, т.е. f (x) эквивалентна С при х → +∞. Из второго признака сравнения следует, что ряд ведет себя так же, как ряд 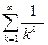: он расходится, если λ ≤ 1, и сходится, если λ > 1.

Пример 8. Исследуем на сходимость ряд . Запишем его производящую функцию: 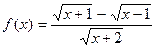. Выделим ее главную часть при х→ +∞:

~

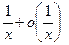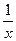= ~ , х→ +∞.

Итак, С = 1, λ = 1, поэтому рассматриваемый ряд ведет себя так же, как гармонический ряд 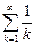, т.е. расходится.

Теорема 4. (Признак Даламбера) Пусть { a _k} – последовательность положительных чисел, и пусть 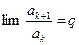, где q – либо неотрицательное число, либо + ∞. Тогда: 1) если 0≤ q < 1, то ряд сходится; 2) если q > 1 или q =+ ∞, то ряд расходится.

► 1) Пусть р – число, удовлетворяющее неравенствам q < p < 1. По теореме о стабилизации знака неравенства ([3], п. 3.3) найдется натуральное k_р такое, что при всех k > k_р справедливо 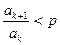, т.е. а _k+1 < p a _k. Отсюда при k = k_p+1 получим при k = k_p+2 получим 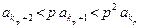, при k= k_p+3 будет и т.д. Вообще, при всяком натуральном m справедливо неравенство 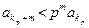. Рассмотрим два ряда: и . Для их общих членов справедливо неравенство 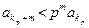, причем ряд с бóльшим общим членом сходится, ибо его члены образуют геометрическую прогрессию, знаменатель р которой меньше единицы. По первому признаку сравнения сходится ряд , который представляет собой остаток ряда ; значит, этот последний ряд сходится.

2) И в случае q > 1, и в случае q = + ∞ найдется натуральное k₀ такое, что при всех k > k₀ справедливо , т.е. начиная с номера k₀ члены пос- ледовательности { a_k } возрастают, поэтому эта последовотельность не стремится к нулю. Значит, ряд расходится. ◄

Замечание. В случае q = 1 признак Даламбера не дает ответа на вопрос о сходимости ряда: если , ряд может оказаться сходящимся, но может окзаться и расходящимся.

Пример 9. Применим признак Даламбера к ряду 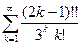: a _k = ,

.

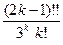Значит, ряд сходится.

Теорема 5. (Радикальный признак Коши) Пусть { a _k} – последовательность неотрицательных чисел, и пусть , где q – либо неотрицательное число, либо +∞. Тогда: 1) если 0 ≤ q < 1, то ряд сходится, 2) если q > 1 или q = + ∞, то ряд расходится.

► 1) Пусть р – число, удовлетворяющее неравенствам q < р < 1. Най- дется натуральное k_р такое, что при всех k > k_р справедливо , т.е. a _k< < . По первому признаку сравнения отсюда следует, что ряд (остаток ряда ) сходится, так как его члены меньше соответствующих членов бесконечно убывающей геометрической прогрессии. Поскольку сходится остаток, то сходится и сам ряд.

2) И в случае q > 1, и в случае q =+ ∞ найдется натуральное k₀ такое, что при всех k > k₀ справедливо ; поэтому при указанных k Значит, последовательность { a_k } не может стремиться к нулю; ряд расходится.◄

Замечание. При q = 1 радикальный признак Коши не не дает ответа на вопрос о сходимости ряда: в этом случае ряд может оказаться сходящимся, но может и расходиться.

Пример 10. Применим радикальный признак Коши к ряду : =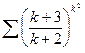

Следовательно, ряд расходится.

Дата добавления: 2015-07-02