
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод наименьших квадратов
|
|
|
|
ВВЕДЕНИЕ
Настоящие методические указания предназначены для студентов специальности 120100 всех форм обучения и содержит варианты индивидуальных заданий с примерами их выполнения.
Задания для выполнения практической работы выбирают согласно ва-рианту, номер которого совпадает с порядковым номером студента в жур-нале.
Метод наименьших квадратов (МНК) относится к методам аппроксимации или приближенного восстановления функции по известным ее значениям в ряде точек. Пусть в результате эксперимента получен набор данных, между которыми может существовать или отсутствовать функциональная либо структурная связь. Если такая связь существует, то она проявляется в эксперименте в неявном виде, а для использования результатов эксперимента в практических целях неявную зависимость необходимо сделать явной. Следовательно, возникает задача о наилучшем подборе эмпирических формул, которые позволяют аналитически представить данные измерений в точках 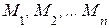 в виде функции. Задача нахождения эмпирических формул состоит из двух этапов.
в виде функции. Задача нахождения эмпирических формул состоит из двух этапов.
Первым этапом при записи аналитического выражения, аппроксимирующего требуемую зависимость, является нанесение экспериментальных точек на график в прямоугольной системе координат. В результате будет получена диаграмма разброса, из которой часто удается визуально выделить кривую и определить соответствующую ей функциональную зависимость, то есть определить вид эмпирической формулы.
На втором этапе подбираются параметры эмпирической формулы так, чтобы подобранная функция наилучшим образом отвечала данным, полученным в результате измерений.
Рассмотрим особенности анализа результатов эксперимента на примере построения линейной модели для случая, когда имеется одна зависимая переменная  и одна независимая переменная
и одна независимая переменная 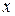 .
.
|
|
|
Результаты измерений, полученные в виде пар значений переменных 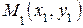 ,
, 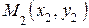 …
… 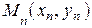 , изображены на рисунке 1.
, изображены на рисунке 1.

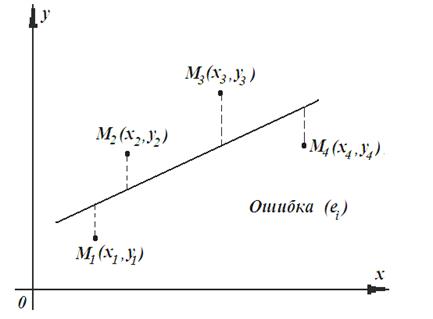
Рис. 1. К построению регрессионной модели методом наименьших квадратов
Сделаем предположение, что зависимость между переменными 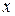 и
и  - линейная, то есть уравнение линии представим в виде:
- линейная, то есть уравнение линии представим в виде:
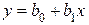 (1)
(1)
Требуется получить такие значения коэффициентов 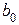 и
и 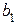 , при которых сумма квадратов ошибок будет минимальной. На рисунке 1 ошибка
, при которых сумма квадратов ошибок будет минимальной. На рисунке 1 ошибка 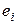 для каждой экспериментальной точки
для каждой экспериментальной точки 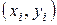 равна расстояниям по вертикали от этой точки до прямой линии.
равна расстояниям по вертикали от этой точки до прямой линии.
Обозначим: 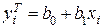 , где
, где 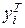 – величина, предсказываемая моделью, заданной уравнением (1). Тогда выражение для ошибок будет иметь вид:
– величина, предсказываемая моделью, заданной уравнением (1). Тогда выражение для ошибок будет иметь вид: 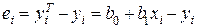 , а функция ошибок:
, а функция ошибок: 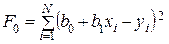 .
.
Для получения коэффициентов 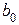 и
и 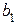 , при которых
, при которых 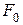 будет минимальной, приравняем нулю частные производные данной функции
будет минимальной, приравняем нулю частные производные данной функции 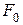 .
.
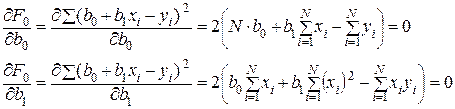
Получена система двух линейных алгебраических уравнений, которая называется системой нормальных уравнений. Решая эту систему, получим 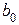 и
и 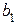 .
.
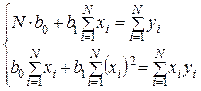 (2)
(2)
Тогда коэффициенты 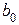 и
и 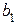 равны:
равны:
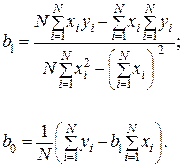 (3)
(3)
В общем случае, когда эмпирическую функцию представляют в ви-
де полинома 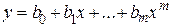 , система нормальных уравнений будет
, система нормальных уравнений будет
иметь следующий вид:
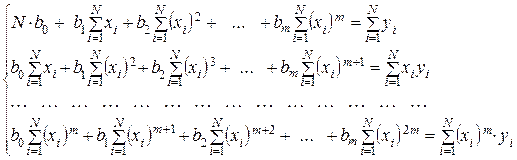 (4)
(4)
Частным случаем является полином вида 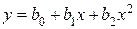 , где
, где 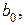
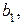
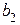 - коэффициенты полинома. Система нормальных уравнений вида (4), для данного полинома (
- коэффициенты полинома. Система нормальных уравнений вида (4), для данного полинома (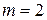 ):
):
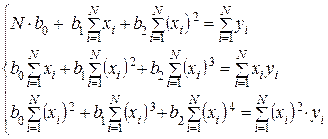 (5)
(5)
Определяют коэффициенты полинома 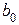 ,
, 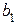 ,
, 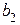 на основании системы уравнений (5), которую можно решить любым известным методом решения систем уравнений из курса «Высшей математики».
на основании системы уравнений (5), которую можно решить любым известным методом решения систем уравнений из курса «Высшей математики».
Для оценки точности совпадения теоретических 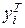 и экспериментальных
и экспериментальных 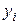 данных следует определить среднюю квадратическую ошибку на единицу веса:
данных следует определить среднюю квадратическую ошибку на единицу веса:
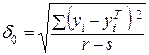 , (6)
, (6)
где 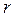 - число вычисляемых (табличных) значений;
- число вычисляемых (табличных) значений; 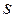 – число параметров.
– число параметров.
В случае, когда экспериментальная кривая не является многочленом первой или второй степени, можно с помощью подходящей замены переменной свести ее к линейной функции. Так, например, пусть сглаживающая кривая принадлежит классу показательных функций и характеризуется двумя параметрами 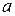 и
и 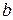 , то есть имеет вид:
, то есть имеет вид:
|
|
|
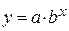 (7)
(7)
Прологарифмировав выражение (7), получим:
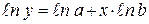 (8)
(8)
Введем новые обозначения для параметров и переменных
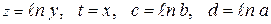
В новых обозначениях уравнение (8) будет линейным относительно переменных 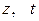 :
:
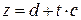 (9)
(9)
Сделав пересчет выборочных значений наблюдаемых случайных величин, получим набор 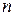 пар чисел
пар чисел 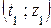 ,
, 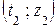 , …,
, …, 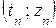 , где
, где 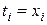 ,
, 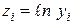 ,
, 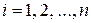 , которые принимаем за новые исходные данные, отвечающие величинам
, которые принимаем за новые исходные данные, отвечающие величинам 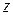 и
и 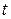 , связанным между собой линейным уравнением (9). Параметры
, связанным между собой линейным уравнением (9). Параметры 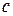 и
и 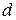 этой сглаживающей прямой (9) определяем методом наименьших квадратов, решая систему (2) (в новых обозначениях) относительно
этой сглаживающей прямой (9) определяем методом наименьших квадратов, решая систему (2) (в новых обозначениях) относительно 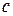 и
и 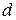 . Найденные значения параметров
. Найденные значения параметров 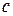 и
и 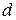 подставляем и вычисляем искомые значения параметров
подставляем и вычисляем искомые значения параметров 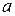 и
и 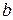 :
: 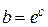 ,
, 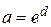 . В результате получаем уравнение сглаживающей кривой (7). Степенную, показательную, гиперболическую, логарифмическую зависимости сводим к линейной, применяя следующие замены переменных (табл. 1).
. В результате получаем уравнение сглаживающей кривой (7). Степенную, показательную, гиперболическую, логарифмическую зависимости сводим к линейной, применяя следующие замены переменных (табл. 1).
Таблица 1
Сведение зависимостей к линейным путем преобразования координат
| № n|n | Сглаживающая функция | Приведенная функция | Замена переменных |
| 1 | 2 | 3 | 4 |
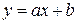
| 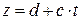
| 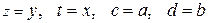
| |
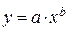
| 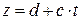
| 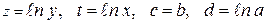
| |
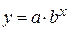
| 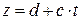
| 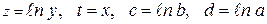
|
Окончание табл.1
| 1 | 2 | 3 | 4 |
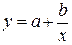
| 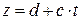
| 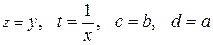
| |
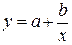
| 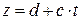
| 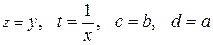
| |
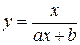
| 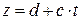
| 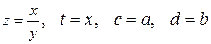
| |
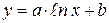
| 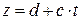
| 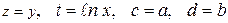
|
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 693; Нарушение авторских прав?; Мы поможем в написании вашей работы!