
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Декодирование принимаемой кодовой комбинации. 1 страница. Процедура исправления ошибок в коде РС является более сложной, чем в двоичном коде БЧХ, поскольку, наряду с определением номера разряда
|
|
|
|
Процедура исправления ошибок в коде РС является более сложной, чем в двоичном коде БЧХ, поскольку, наряду с определением номера разряда, в котором допущена ошибка, необходимо определить значение ошибочно принятого символа. При этом для определения местоположения ошибок можно использовать способы, применяемые для декодирования кодов БЧХ, в том числе и рассмотренный в лабораторной работе №2 алгебраический метод, основанный на использовании алгоритма Питерсона-Горенстейна-Цирлера [4, 3]. Однако объём вычислений при его реализации, связанный в основном с необходимостью решения приведённого в [3] матричного уравнения (11), или, что практически эквивалентно, обращения (т.е. нахождения обратной по отношению к заданной) квадратной матрицы размером 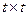 в случае применяемых на практике кодов с высокой исправляющей способностью
в случае применяемых на практике кодов с высокой исправляющей способностью  оказывается чрезмерно большим (число умножений пропорционально
оказывается чрезмерно большим (число умножений пропорционально 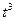 ). Для определения значений ошибок при развитии этого метода понадобится обращение ещё одной квадратной матрицы такого же размера, что удваивает сложность задачи. В связи с этим был разработан способ быстрого декодирования кодов РС, иллюстрируемый алгоритмом, представленным на рис.1. Рассмотрим сущность и методику выполнения основных этапов данного алгоритма на конкретном примере.
). Для определения значений ошибок при развитии этого метода понадобится обращение ещё одной квадратной матрицы такого же размера, что удваивает сложность задачи. В связи с этим был разработан способ быстрого декодирования кодов РС, иллюстрируемый алгоритмом, представленным на рис.1. Рассмотрим сущность и методику выполнения основных этапов данного алгоритма на конкретном примере.
Предположим, что по каналу связи передавалcя двоичный блок кода
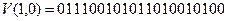 ,
,
представляющий собой двоичный эквивалент разрешённой кодовой комбинации символов кода РС (7,3), обеспечивающего  при
при  , которая в десятичном представлении имеет вид
, которая в десятичном представлении имеет вид
 . (8)
. (8)
Допустим далее, что вследствие воздействия помех блок  превратился в принимаемую кодовую комбинацию
превратился в принимаемую кодовую комбинацию
 , (9)
, (9)
что в символах кода РС можно записать как
|
|
|
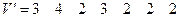 , (10)
, (10)
т.е. произошло две ошибки в 1-м и 5-м разрядах (если считать первым − младший, крайний справа разряд) блока кода РС при фактическом наличии пяти ошибок в принимаемой двоичной последовательности (9). В данной ситуации полином ошибок имеет вид: 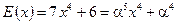 (см. табл.П.2), поскольку
(см. табл.П.2), поскольку 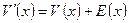 , где
, где 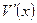 и
и 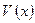 − полиномы, соответствующие блокам кода РС (10) и (8). (Отметим, что в реальной ситуации, моделируемой в лабораторной работе, переданная комбинация
− полиномы, соответствующие блокам кода РС (10) и (8). (Отметим, что в реальной ситуации, моделируемой в лабораторной работе, переданная комбинация  и вид многочлена ошибок неизвестны.)
и вид многочлена ошибок неизвестны.)
Первым этапом в процедуре определения количества ошибок и их исправления является процесс вычисления синдрома принятой кодовой комбинации (блок 1 алгоритма рис.1). Код синдрома 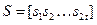 состоит из
состоит из  элементов
элементов  , которые рассчитываются в поле
, которые рассчитываются в поле  как
как
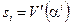 , (11)
, (11)
где
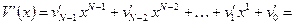
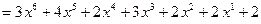 − (12)
− (12)
многочлен над полем  , соответствующий принимаемой кодовой комбинации
, соответствующий принимаемой кодовой комбинации  (10);
(10); 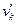 − значение
− значение 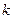 -го разряда (
-го разряда (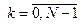 ) блока кода
) блока кода  ;
;  − примитивный элемент поля
− примитивный элемент поля  .
.
Вычисления по формуле (11) удобно выполнить, используя возможности, представляемые пакетом Matlab. Для этого необходимо:
1) в командном окне системы Matlab задать полином  над полем
над полем  , соответствующий принимаемой комбинации
, соответствующий принимаемой комбинации  . В рассматриваемом нами случае приёма
. В рассматриваемом нами случае приёма  (10) (при
(10) (при  ) это можно сделать с использованием команды
) это можно сделать с использованием команды

2) задать вектор 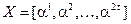 набора степеней примитивного элемента
набора степеней примитивного элемента 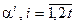 поля
поля  , которые в соответствии с (11) представляют собой значения аргументов
, которые в соответствии с (11) представляют собой значения аргументов  при вычислении
при вычислении  элементов синдрома
элементов синдрома 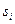 . При этом следует использовать десятичные представления элементов
. При этом следует использовать десятичные представления элементов 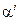 (см. Табл. П.2 и П.3 из [3]). В рассматриваемом примере (при
(см. Табл. П.2 и П.3 из [3]). В рассматриваемом примере (при  ,
,  ) этот вектор задаётся командой
) этот вектор задаётся командой
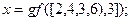
3) с использованием команды 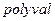 , вычислить вектор элементов синдрома. Команда
, вычислить вектор элементов синдрома. Команда 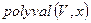 , позволяет оценить значение многочлена
, позволяет оценить значение многочлена  в поле
в поле  , которому принадлежат задаваемые в качестве аргумента значения
, которому принадлежат задаваемые в качестве аргумента значения 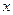 . В нашем примере для расчёта вектора элементов синдрома
. В нашем примере для расчёта вектора элементов синдрома 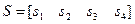 в командном окне системы Matlab следует записать:
в командном окне системы Matlab следует записать:
 ;
;
Выполнение этой команды даёт следующий результат:
|
|
|
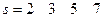 ; (13)
; (13)
Каждое из полученных чисел отражает собой десятичное представление значения соответствующего элемента синдрома в поле 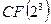 , т.е.
, т.е. 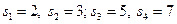 . Отметим, что, если принятая комбинация не содержит ошибок, вектор синдрома будет содержать одни нули. В этом можно убедиться, вычислив синдром передаваемой кодовой комбинации
. Отметим, что, если принятая комбинация не содержит ошибок, вектор синдрома будет содержать одни нули. В этом можно убедиться, вычислив синдром передаваемой кодовой комбинации  (8), выполнив команды
(8), выполнив команды

 .
.
Первая из этих команд позволяет задать полином  над полем
над полем 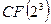 , соответствующий передаваемой комбинации
, соответствующий передаваемой комбинации  (8) а вторая − оценить значение этого многочлена при заданном векторе входных аргументов
(8) а вторая − оценить значение этого многочлена при заданном векторе входных аргументов 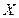 . В результате этого оценивания получается нулевой синдром
. В результате этого оценивания получается нулевой синдром 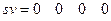 , т.е.
, т.е.  = 0.
= 0.
Следующим этапом процедуры декодирования является определения полинома локаторов ошибок 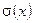 (блок 2 алгоритма на рис. 1), корнями которого являются величины
(блок 2 алгоритма на рис. 1), корнями которого являются величины 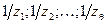 , обратные значениям локаторов ошибок
, обратные значениям локаторов ошибок  , определяющих позиции расположения ошибок в полиноме
, определяющих позиции расположения ошибок в полиноме 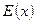 . Ввиду отмеченных выше недостатков рассмотреннного в лабораторной работе 2 алгоритма Питерсона-Горенстейна-Цирлера при быстром декодировании кодов РС эта задача решается на основе алгоритма Берлекэмпа-Месси (блок 2 на рис.1). Идея этого алгоритма базируется на том, что каждая строка матричного уравнения (11) из [3] выражает значение последующего элемента синдрома через
. Ввиду отмеченных выше недостатков рассмотреннного в лабораторной работе 2 алгоритма Питерсона-Горенстейна-Цирлера при быстром декодировании кодов РС эта задача решается на основе алгоритма Берлекэмпа-Месси (блок 2 на рис.1). Идея этого алгоритма базируется на том, что каждая строка матричного уравнения (11) из [3] выражает значение последующего элемента синдрома через  предшествующих (например, первая строка выражает
предшествующих (например, первая строка выражает 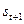 через
через 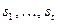 , вторая −
, вторая − 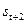 через
через  и т.д.). Этот последовательный процесс описывается выражением
и т.д.). Этот последовательный процесс описывается выражением
 . (14)
. (14)
Отметим, что, в случае, когда в исследуемом блоке кода имеет место 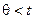 ошибок, соотношение (14) принимает вид:
ошибок, соотношение (14) принимает вид:
 . (15)
. (15)
Выражение (15) можно трактовать как разностное уравнение рекурсивного цифрового фильтра, представляющего собой регистр сдвига неизвестной заранее длины  с коэффициентами
с коэффициентами 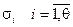 в ветвях обратной связи. Таким образом, задача определения коэффициентов полинома локаторов
в ветвях обратной связи. Таким образом, задача определения коэффициентов полинома локаторов 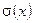 сводится к построению регистра сдвига минимальной длины с обратными связями, отображающими
сводится к построению регистра сдвига минимальной длины с обратными связями, отображающими 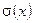 , порождающего первые 2 t членов синдромного многочлена
, порождающего первые 2 t членов синдромного многочлена 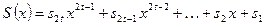 .
.
Не вдаваясь в теоретическое обоснование алгоритма Берлекэмпа-Месси, приводимое, например, в [4], поясним его основное содержание [4,5]. Вначале находят самый короткий регистр сдвига, генерирующий  . Далее проверяют, порождает ли этот регистр также
. Далее проверяют, порождает ли этот регистр также 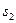 . Если порождает, то данный регистр по-прежнему остается наилучшим решением, и нужно проверить, порождает ли он следующие символы синдромного многочлена. На каком-то шаге очередной символ уже не будет генерироваться. В этот момент нужно изменить регистр таким образом, чтобы он:
. Если порождает, то данный регистр по-прежнему остается наилучшим решением, и нужно проверить, порождает ли он следующие символы синдромного многочлена. На каком-то шаге очередной символ уже не будет генерироваться. В этот момент нужно изменить регистр таким образом, чтобы он:
|
|
|
1) правильно предсказывал следующий символ,
2) не менял предсказание предыдущих символов,
3) увеличивал длину регистра на минимально возможную величину.
Процесс вычисления продолжается до тех пор, пока не будут порождены первые 2 t символов синдрома.
Алгоритм строится на основе итеративной процедуры. При каждой итерации должны сохраняться как многочлен связей 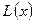 , так и добавка
, так и добавка  . Для каждого новой составляющей
. Для каждого новой составляющей  предусматривается проверка правильности предсказания этого символа текущим многочленом связи. Если предсказание правильно, то многочлен связей не меняется, а добавка умножается на x. Если предсказание неправильно (ошибка
предусматривается проверка правильности предсказания этого символа текущим многочленом связи. Если предсказание правильно, то многочлен связей не меняется, а добавка умножается на x. Если предсказание неправильно (ошибка  ), то изменяют текущий многочлен связей, прибавляя к нему добавку. После этого проверяют, увеличилась ли длина регистра. Если она не увеличилась, то текущую добавку оставляют. Если длина регистра возрастает, то лучшей добавкой считают предыдущий многочлен связей. Для недвоичных полей добавку нормируют, чтобы ошибка стала равной 1. Далее при каждом исправлении эту нормализованную добавку умножают на значение текущей ошибки.
), то изменяют текущий многочлен связей, прибавляя к нему добавку. После этого проверяют, увеличилась ли длина регистра. Если она не увеличилась, то текущую добавку оставляют. Если длина регистра возрастает, то лучшей добавкой считают предыдущий многочлен связей. Для недвоичных полей добавку нормируют, чтобы ошибка стала равной 1. Далее при каждом исправлении эту нормализованную добавку умножают на значение текущей ошибки.
Рассмотренный алгоритм изображён на рис.2 (блоки 1 − 7). По найденному с его применением полиному локаторов ошибок, как отмечалось выше, можно определить их местонахождение в принятой комбинации. Для определения значений ошибок при быстром декодировании используется алгоритм Форни. Для его реализации вначале необходимо найти многочлен значений ошибок  (блок 3 на рис.1), определяемый выражением:
(блок 3 на рис.1), определяемый выражением:
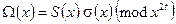 . (16)
. (16)
Вместе с тем, как показано в [5], вычисления по формуле (16) можно заменить дополнением к рассмотренному алгоритму Берлекэмпа – Месси, позволяющим одновременно с нахождением значения многочлена локаторов ошибок 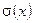 находить многочлен значений ошибок
находить многочлен значений ошибок  . Это дополнение на рис. 2 представлено блоками 8 − 10. Его идея заключается в том, что, поскольку
. Это дополнение на рис. 2 представлено блоками 8 − 10. Его идея заключается в том, что, поскольку  находится умножением
находится умножением 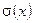 на
на 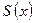 , можно задать последовательность многочленов
, можно задать последовательность многочленов 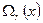 , удовлетворяющих тем же рекуррентным соотношениям, что и многочлены
, удовлетворяющих тем же рекуррентным соотношениям, что и многочлены  . Обозначая добавку при нахождении
. Обозначая добавку при нахождении  через
через  , имеем:
, имеем:
|
|
|

что и реализуется блоками 8 − 10 алгоритма рис.2 при начальных условиях  и
и  . Тот факт, что в (16) умножение осуществляется по
. Тот факт, что в (16) умножение осуществляется по 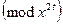 , в алгоритме учитывается соответствующим диапазоном изменения переменной цикла
, в алгоритме учитывается соответствующим диапазоном изменения переменной цикла  , задающей число шагов итерации.
, задающей число шагов итерации.
Рассмотрим, как реализуются вычисления, предписываемые алгоритмом рис. 2, применительно к нашему примеру.
1. В соответствии с блоком 1 алгоритма задаёмся начальными условиями: 
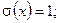

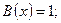

 .
.
2. Первая итерация: 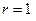 .
.
Приведённая в блоке 2 алгоритма рис.2 формула для вычисления ошибки 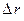 предполагает проведение вычислений по правилам поля
предполагает проведение вычислений по правилам поля  (в рассматриваемом примере −
(в рассматриваемом примере − 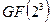 ), причём использованное в ней обозначение
), причём использованное в ней обозначение 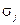 соответствует
соответствует  -му коэффициенту полинома локаторов, который в конечном итоге имеет вид:
-му коэффициенту полинома локаторов, который в конечном итоге имеет вид:  ; значения
; значения 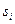 были вычислены ранее (см. (13)). Итак, при
были вычислены ранее (см. (13)). Итак, при 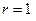 , кода в соответствии с начальным условием
, кода в соответствии с начальным условием 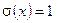 , имеем:
, имеем:
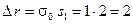 .
.
Правила вычислений в поле 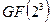 изложены в [2], вместе с тем их можно выполнить в системе Matlab, записав:
изложены в [2], вместе с тем их можно выполнить в системе Matlab, записав:
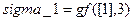 ;
;
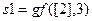 ;
;
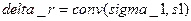
В результате выполнения этих команд в командном окне появится результат:  .
.
Условие  не выполняется, поэтому переходим к блоку 4 алгоритма и записываем:
не выполняется, поэтому переходим к блоку 4 алгоритма и записываем:
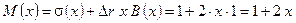 .
.
Условие  выполняется (
выполняется (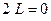 и
и  ), поэтому переходим к выполнению блока 6 и вычисляем:
), поэтому переходим к выполнению блока 6 и вычисляем:
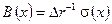 .
.
При выполнении этой операции вычисления производятся по правилам поля 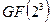 . В системе Matlab, учитывая, что на данной итерации
. В системе Matlab, учитывая, что на данной итерации 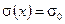 это можно сделать с помощью команды
это можно сделать с помощью команды
 .
.
В результате её выполнения получаем  . Далее в соответствии с предписаниями блока 6 алгоритма имеем:
. Далее в соответствии с предписаниями блока 6 алгоритма имеем:
 ;
;
 .
.
После этого корректируем многочлен значений ошибок (блок 8 алгоритма):
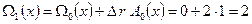 .
.
Условие  не выполняется (
не выполняется ( ;
; 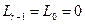 ), поэтому вычисляем
), поэтому вычисляем  как (блок 10)
как (блок 10)
 .
.
Вычисления, предписываемые блоком 10, также нужно производить по правилам поля 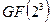 , однако умножение на ноль в любом поле даёт ноль. Поскольку условие
, однако умножение на ноль в любом поле даёт ноль. Поскольку условие  не выполняется, переходим к следующей итерации.
не выполняется, переходим к следующей итерации.
3. Вторая итерация:  .
.
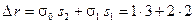 .
.
Для выполнения этих вычислений по правилам поля 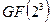 в системе Matlab нужно записать следующие команды:
в системе Matlab нужно записать следующие команды:
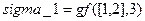 ;
;
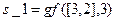 ;
;
 ;
;
 .
.
В результате их выполнения получаем: 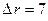 .
.
Условие  не выполняется, поэтому переходим к блоку 4 алгоритма и вычисляем (по правилам поля
не выполняется, поэтому переходим к блоку 4 алгоритма и вычисляем (по правилам поля 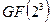 ):
):
 .
.
Условие  не выполняется (
не выполняется ( и
и  ), поэтому переходим к последовательному выполнению блоков 5 и 7 и записываем:
), поэтому переходим к последовательному выполнению блоков 5 и 7 и записываем:
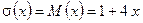
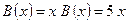 .
.
Далее корректируем многочлен значений ошибок (блок 8 алгоритма):
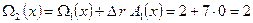 .
.
Условие  выполняется (
выполняется (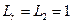 ;
; 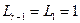 ), поэтому вычисляем
), поэтому вычисляем  как (блок 9)
как (блок 9)
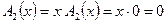 .
.
Поскольку условие  не выполняется, переходим к следующей итерации.
не выполняется, переходим к следующей итерации.
4. Третья итерация:  .
.
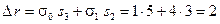 .
.
Условие  не выполняется, поэтому переходим к блоку 4 алгоритма и вычисляем:
не выполняется, поэтому переходим к блоку 4 алгоритма и вычисляем:
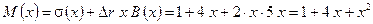 .
.
Условие  выполняется (
выполняется ( и
и 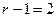 ), поэтому переходим к выполнению блока 6 и получаем:
), поэтому переходим к выполнению блока 6 и получаем:
 .
.
 ;
;
 .
.
После этого корректируем многочлен значений ошибок (блок 8 алгоритма):
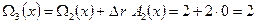 .
.
Условие  не выполняется (
не выполняется (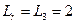 ;
; 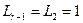 ), поэтому вычисляем
), поэтому вычисляем  как (блок 10)
как (блок 10)
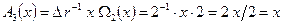 .
.
Поскольку условие  не выполняется, переходим к следующей итерации.
не выполняется, переходим к следующей итерации.
5. Четвёртая итерация:  .
.
 .
.
В системе Matlab эти вычисления можно выполнить следующим образом:
 ;
;
 ;
;
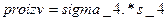 ;
;
 .
.
Условие  не выполняется, поэтому переходим к блоку 4 алгоритма и вычисляем:
не выполняется, поэтому переходим к блоку 4 алгоритма и вычисляем:
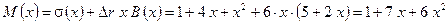 .
.
Условие  не выполняется (
не выполняется ( и
и 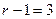 ), поэтому переходим к последовательному выполнению блоков 5 и 7 и записываем:
), поэтому переходим к последовательному выполнению блоков 5 и 7 и записываем:
 ;
;
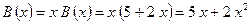 .
.
Далее корректируем многочлен значений ошибок (блок 8 алгоритма):
 .
.
Условие  выполняется (
выполняется ( ;
;  ), поэтому вычисляем
), поэтому вычисляем  как (блок 9)
как (блок 9)
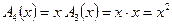 .
.
Поскольку условие  выполняется, выполнение алгоритма на этом заканчивается.
выполняется, выполнение алгоритма на этом заканчивается.
Таким образом, полином локаторов ошибок имеет вид:
 , (17)
, (17)
а многочлен значений ошибок −
 . (18)
. (18)
В корректности полученных результатов можно убедиться, вычислив  по формуле (16). С использованием системы Matlab это можно сделать с помощью команд:
по формуле (16). С использованием системы Matlab это можно сделать с помощью команд:
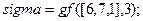
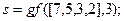
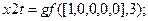

Возвращаемый при этом вектор  соответствует вычисленному полиному
соответствует вычисленному полиному  .
.
В рассматриваемом примере в принимаемой комбинации  (10) присутствуют две ошибки. В полученном результате об этом говорит тот факт, что степень полинома
(10) присутствуют две ошибки. В полученном результате об этом говорит тот факт, что степень полинома  равна 2. В том случае, если число ошибок
равна 2. В том случае, если число ошибок 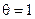 , она была бы на 1 меньше. Таким образом, о числе ошибок
, она была бы на 1 меньше. Таким образом, о числе ошибок  (при условии
(при условии 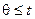 ) можно судить по степени полученного многочленов локаторов.
) можно судить по степени полученного многочленов локаторов.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 645; Нарушение авторских прав?; Мы поможем в написании вашей работы!