Закон Ома в операторной форме

Законы Кирхгофа в операторной форме.

Первый закон Кирхгофа: алгебраическая сумма токов ветвей сходящихся в узле в любой момент времени равна нулю

.

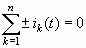Преобразуем по Лапласу обе части этого равенства, учитывая свойство линейности (3.2). Тогда получим первый закон Кирхгофа в операторной форме

.

Его формулировка: алгебраическая сумма операторных токов ветвей, сходящихся в узле, равна нулю.

Второй закон Кирхгофа: алгебраическая сумма напряжений на ветвях замкнутого контура в любой момент времени равна нулю

.

На основании свойства линейности после преобразования по Лапласу этого равенства получим второй закон Кирхгофа в операторной форме

.

Его формулировка: алгебраическая сумма операторных напряжений на ветвях замкнутого контура равна нулю.

Введем в рассмотрение операторное сопротивление Z(p) участка цепи, которое определим как отношение операторного напряжения к операторному току участка цепи при нулевых начальных условиях:

(3.9)

где - операторная проводимость.

Рассмотрим в качестве простейших участков цепи отдельные элементы: резистор, катушку индуктивности и конденсатор.

Резистор. Мгновенные ток и напряжение связаны законом Ома: . Преобразуем обе части этого равенства по Лапласу и получим закон Ома для резистора в операторной форме:

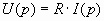(3.10)

Операторные сопротивления и проводимость:

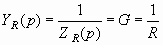
(3.11)

Катушка индуктивности. Напряжение u(t) и ток i(t) в катушке связаны соотношением 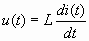. Будем предполагать нулевые начальные условия i_L(0)=0. Преобразуем обе части этого равенства по Лапласу. Тогда согласно свойствам (3.1) и (3.2) получим:

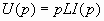
(3.12)

Полученное соотношение, также как и (3.10), является алгебраическим (без операций дифференцирования или интегрирования) и его можно назвать законом Ома в операторной форме для индуктивности. При этом операторные сопротивление и проводимость индуктивности

; .

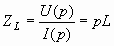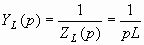(3.13)

Конденсатор. Связь между током и напряжением на емкостном элементе . При нулевых начальных условиях (u_c(0)=0) после преобразования этого равенства по Лапласу получим закон Ома в операторной форме для емкостного элемента:

; .

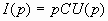(3.14)

Соответствующие операторные сопротивление и проводимость

; .

(3.15)

Таким образом, закон Ома в операторной форме выполняется для всех трех элементов электрических цепей и может быть записан в обобщенном виде:

; ; ;

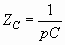(3.16)

Нетрудно заметить связь операторных и комплексных сопротивлений. Напомним, что комплексные сопротивления элементов: 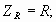. Очевидно, что их можно получить из операторных путем замены переменной, а именно

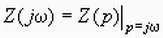
(3.17)

Несмотря на такую аналогию комплексных и операторных сопротивлений, между ними имеется принципиальная разница. Комплексные сопротивления вводятся для установившегося режима гармонических колебаний, когда все токи и напряжения являются гармоническими функциями, а операторные - для самого общего переходного режима, в котором токи и напряжения могут быть произвольными функциями времени.

Рассмотрим соотношения между операторными токами и напряжениями на элементах при ненулевых начальных условиях 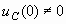и . Очевидно, что изменения коснуться соответствующих уравнений для реактивных элементов, реальные токи и напряжения в которых связаны дифференциальными соотношениями.

Так для индуктивного элемента 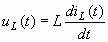и после преобразования этого равенства по Лапласу согласно свойству (3.3) при ненулевых начальных условиях получим:

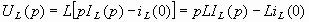
(3.18)

Полученному уравнению соответствует так называемая операторная схема замещения индуктивности, которая представлена на рис. 3.1. Она содержит элемент с операторным сопротивлением , который моделирует падение напряжения от прохождения тока 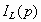(первое слагаемое в (3.18)), и источник напряжения (моделирующий второе слагаемое в (3.18)).

Аналогично для емкости после преобразования при ненулевых начальных условиях получим

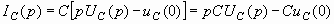
или

(3.19)

В соответствии с (3.19) на рис. 3.2 представлена операторная схема замещения емкостного элемента.

Она содержит элемент с операторным сопротивлением 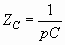и источник операторного напряжения 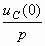, обусловленный ненулевым начальным условием.

Дата добавления: 2015-07-02