T-Распределение

Степень приближения выборочной дисперсии к генеральной зависит от числа степеней свободы f, определяемой выражением:

f = n-1

где n – число измерений, равное числу параллельных проб.

Чем меньше число степеней свободы, тем менее надежной характеристикой генеральной дисперсии s² является выборочная дисперсия S². При нормальном распределении появление больших погрешностей менее вероятно, чем малых, поэтому при уменьшении числа параллельных проб вероятность появления больших погрешностей уменьшается. Неучет этого приводит к необъективному, заниженному значению погрешности. Эта ненадежность, связанная с числом определений (параллельных проб), учитывается t-распределением Стьюдента, в котором предусматривается большая вероятность появления больших погрешностей, а вероятность малых меньше, чем в нормальном распределении.

Как и нормальное распределение, t-распределение симметрично и имеет максимум при том же значении абсциссы, при котором он был при нормальном распределении. Однако такие характеристики кривой t-распределения, как высота и ширина, зависят от числа степеней свободы, т.е. от числа измерений (рис. 5.1).

Рис. 5.1. Кривая распределения: 1 – f =∞, 2 – f=7, 3 – f=3

Как показывает рис. 5.1, чем меньше число степеней свободы, тем меньше крутизна кривой и тем медленнее она сближается с осью абсцисс при одном и том же стандартном отклонении. При f®¥ t-распределение переходит в нормальное распределение. Практически эта разница становится малозаметной уже при f ³ 20.

Если в случае нормального распределения при большом числе измерений доверительный интервал m±2s реализовался с 95 %-ной доверительной вероятностью, то при малом числе измерений заданная величина доверительной вероятности реализуется в доверительном интервале 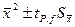,где t_P,f – коэффициент Стьюдента, учитывающий разницу в нормальном и t-распределении и при данной вероятности Р, зависящий от числа степеней свободы. Индекс Р у t указывает на фиксированную вероятность, f – число степеней свободы. Числовые значения коэффициента t_P,f при различных Р и f приведены в таблице 1. Как видно, при Р =95 % и f =20 коэффициент t_P,f =2,09, т.е. близок к 2, характерному для нормального распределения.

Таблица 1

Коэффициенты Стьюдента

Число степеней свободы, f=n-1	Доверительная вероятность, Р
0,75	0,90	0,95	0,98	0,99
	2,41	6,31	12,71	31,82	63,66
	1,60	2,92	4,30	6,97	9,92
	1,42	2,35	3,18	4,54	5,84
	1,34	2,13	2,78	3,75	4,60
	1,30	2,01	2,57	3,37	4,03
	1,27	1,94	2,45	3,14	3,71
	1,25	1,89	2,36	3,00	3,50
	1,24	1,86	2,31	2,90	3,36
	1,23	1,83	2,26	2,82	3,25
	1,22	1,81	2,23	2,76	3,17
	1,21	1,80	2,20	2,72	3,11
	1,21	1,78	2,18	2,68	3,05
	1,20	1,77	2,16	2,65	3,01
	1,20	1,76	2,14	2,62	2,98
	1,20	1,75	2,13	2,60	2,95
	1,19	1,75	2,12	2,58	2,92
	1,19	1,74	2,11	2,57	2,90
	1,19	1,73	2,10	2,55	2,88
	1,19	1,73	2,09	2,54	2,86
	1,18	1,73	2,09	2,53	2,85
	1,17	1,70	2,04	2,46	2,75
	1,17	1,68	2,02	2,42	2,70
	1,16	1,67	2,00	2,39	2,66
	1,16	1,66	1,98	2,36	2,62
∞	1,15	1,64	1,96	2,33	2,58

При малых значениях f разница между нормальным и t-pacпределением весьма существенна, например, для f =3 и Р =95 % коэффициент t_P,_f =3,18 вместо 2 для нормального распределения. Вероятную относительную погрешность среднего арифметического (относительное отклонение) рассчитывают по формуле:

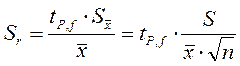
При заданной доверительной вероятности Р доверительный интервал составляет:

(5.1)

,

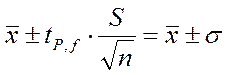если

(5.2)

,

где s – наиболее вероятная погрешность анализа при данной доверительной Р и числе степеней свободы f.

Истинное содержание, или генеральное среднее, находится в пределах от 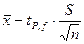до , которые называют также доверительными границами. Поскольку вероятность получения результата, выходящего за эти пределы, остается с риском, отличным от нуля (1-Р), доверительный интервал необходимо характеризовать доверительной вероятностью, которую следует указывать так же, как и число степеней свободы. Доверительный интервал результата анализа обычно вычисляют для доверительной вероятности Р =95 %.

Как показывает уравнение (5.1), чем больше число определений п, тем меньше доверительный интервал при данной доверительной вероятности Р, т.е. тем выше точность анализа.

Например, при доверительной вероятности Р =95 % для двух параллельных определений доверительный интервал в соответствии с уравнением (5.1) составляет 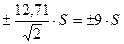, для трех это бу­дет , для четырех 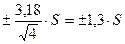и для пяти . Как видно, наиболее эффективное влияние на доверительный интервал и уменьшение погрешности оказывает увеличение числа определений лишь до 4-5 параллельных; дальнейшее увеличение числа параллельных проб оказывает уже значительно меньшее влияние. Поэтому больше четырех параллельных определений выполняют только в специальных случаях, например в некоторых арбитражных анализах.

Пример: найдем доверительный интервал для результата четырех параллельных определений олова в бронзе при среднем содержании 4,725 % и стандартном отклонении 0,112 %. По таблице 1 находим для доверительной вероятности Р =0,95 и числа степеней свободы коэффициент Стьюдента t_{0,95; 3}=3,18. Тогда при Р =0,95 вероятная погрешность .

При расчетах окончательный результат обычно округляют. Округление следует проводить с соблюдением определенных правил, так как излишнее округление может ухудшить результаты анализа, а вычисления с неоправданно большим числом десятичных знаков без округления требуют больших, но напрасных затрат труда, поскольку не улучшают реальной точности результата.

При округлении обычно придерживаются следующих правил. Если за последней округляемой стоит цифра меньше 5, округляемую цифру оставляют без изменения (округление с уменьшением), а если больше 5, округляемую цифру увеличивают на единицу (округление с увеличением), например 4,7252 округляют до 4,725, но 4,7257 округляют до 4,726. Несколько сложнее правила округления, когда за последней округляемой цифрой стоит 5. Если за этой цифрой 5 нет более никаких цифр, то округляют до четной цифры, например, 4,7255 ® 4,726, но 4,7245 ® 4,724. Если за цифрой 5 имеется еще какая-либо отличная от нуля цифра, то округляют с увеличением, однако если 5 получено уже в результате округления, то округляют с уменьшением, т.е. 5 просто отбрасывают. Например, 4,72551 ® 4,726, но 4,72548 ® 4,7255 ® 4,725.

В нашем примере среднее арифметическое составляет 4,725, средняя квадратичная погрешность 0,112 с погрешностью 0,046. При Р =0,95 и трех степенях свободы это приводит к вероятной погрешности 0,178 с погрешностью 0,073.

При окончательном округлении результатов сначала округляют погрешность. Часто, но не всегда принимают во внимание, что, если первая цифра погрешности близка к единице, в значении погрешности приводят две значащие цифры, а если к 9, то одну, хотя, конечно, такой подход не является обязательным и может измениться в зависимости от содержания компонента, величины погрешности и некоторых других обстоятельств, например условий заказчика и т.д.

В рассматриваемом случае погрешность округляют до ±0,18. Среднее значение округляют до 4,72, поскольку результат анализа следует приводить с таким числом знаков, чтобы одна или две последние цифры характеризовали тот же разряд или разряды, к которым относится погрешность. Таким образом, доверительный интервал среднего будет находиться в пределах 4,72±0,18, т.е. от 4,54 до 4,90.

Указание 5-6 значащих цифр в результатах анализа обычно свидетельствует о не критическом отношении к погрешности числа. Необходимо напомнить, что нули, предшествующие первой цифре, отличной от нуля, значащими не являются.

С помощью формулы (5.2) и таблицы 1 можно также найти число параллельных проб, которое следует взять для анализа, чтобы погрешность определения не превышала какого-то заданного значения.

Пусть, например, погрешность определения олова в бронзе необходимо снизить до ±0,10 % (абсолютных), вместо достигнутой ±0,18 % при прежнем стандартном отклонении отдельного измерения ±0,112 % и доверительной вероятности Р =0,95. Из уравнения (5.2) находим:

При n =7 получаем 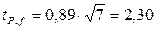. По данным таблицы 1 при f =6 это соответствует вероятности Р =0,95, поэтому семи параллельных измерений недостаточно. Если п =8, то 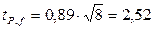. Для f =7 и Р =0,95 по таблице 1 находим коэффициент Стьюдента, он равен 2,36. Следовательно, доверительная вероятность в этом случае будет несколько превышать Р =0,95. Таким образом, при 8 параллельных определениях требование к погрешности анализа будет удовлетворено.

Из формулы (5.2) также следует неожиданный и интересный вывод о значении экспрессности при оценке точности анализа. Если, например, выполнение двух параллельных определений одним методом занимает 2 часа при средней квадратичной погрешности S, а другой более быстрый метод дает погрешность вдвое большую, но позволяет сделать за 2 часа четыре параллельных определений, то при одних и тех же затратах времени погрешность в первом случае будет равна ,а во втором – 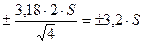, т.е. почти в 3 раза меньшей. Таким образом, выигрыш в точности за счет числа параллельных определений с избытком перекрывает потери за счет увеличения погрешности единичного определения.

Таким образом, оценка измеряемой величины является наилучшей, если она несмещенная, состоятельная и эффективная. При несмещенной оценке ее математическое ожидание равно измеряемой величине, т.е. при нормальном распределении равно среднему арифметическому. Оценку называют состоятельной, если с увеличением числа параллельных измерений она приближается к истинному значению измеряемой величины. И, наконец, оценка эффективна, если ее среднее квадратическое отклонение меньше среднего квадратического отклонения любой другой оценки этой измеряемой величины.

Дата добавления: 2015-07-02