
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод золотого перетину
|
|
|
|
Як відомо, золотим перетином відрізку називається поділ відрізка на дві нерівні частини, щоб відношення довжини всього відрізку до довжини його більшої частини дорівнювало відношенню довжини більшої частини відрізка до довжини його меншої частини.
Неважко перевірити, що золотий перетин відрізку 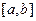 будується двома точками
будується двома точками
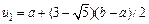
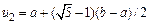 ,
,
які розміщені симетрично відносно середини відрізку, причому  .
.
Відзначимо також, що точка 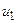 в свою чергу будує золотий перетин відрізку
в свою чергу будує золотий перетин відрізку 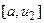 , так як
, так як 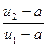 =
= 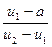 .
.
Аналогічно точка 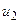 будує золотий перетин відрізка
будує золотий перетин відрізка 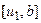 . Спираючись на цю властивість золотого перетину, опишемо відповідний метод.
. Спираючись на цю властивість золотого перетину, опишемо відповідний метод.
Покладемо 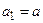 ,
, 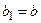 . На відрізку
. На відрізку 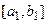 візьмемо точки
візьмемо точки 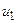 ,
, 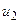 , які будують золотий перетин, і обчислимо значення
, які будують золотий перетин, і обчислимо значення 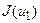 ,
, 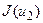 . Далі, якщо
. Далі, якщо  , то покладемо
, то покладемо 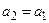 ,
, 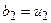 ,
, 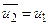 ; якщо ж
; якщо ж 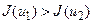 , то покладемо
, то покладемо 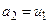 ,
, 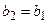 ,
,  . Так як функція
. Так як функція 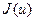 унімодальна на
унімодальна на 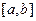 , то відрізок
, то відрізок 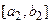 має хоча б одну спільну точку з множиною
має хоча б одну спільну точку з множиною 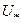 точок мінімуму
точок мінімуму 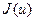 на [a, b]. Крім того,
на [a, b]. Крім того, 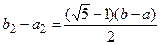 , а та-кож
, а та-кож 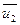 належить відрізку
належить відрізку 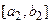 . В цій точці
. В цій точці 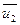 відоме значення
відоме значення

і вона будує золотий перетин відрізка 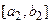 .
.
Припустимо, що все відомі точки 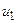 ,
,  ,
,  , обчислені значення
, обчислені значення 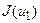 ,
,  ,
, 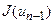 , знайдено відрізок
, знайдено відрізок 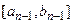 такий, що
такий, що
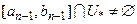 ,
,
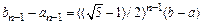 ,
,
і відома точка 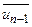 , яка будує золотий перетин відрізка
, яка будує золотий перетин відрізка 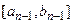 і така що
і така що
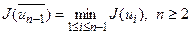 .
.
Тоді в якості наступної точки візьмемо точку
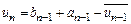 ,
,
яка також будує золотий перетин відрізка 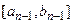 , обчислимо значення
, обчислимо значення 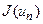 .
.
Нехай для визначенності 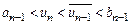 (випадок
(випадок 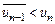
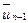 < u
< u 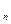 розглядається аналогічно). Якщо
розглядається аналогічно). Якщо 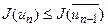 , то покладемо
, то покладемо
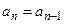 ,
,  ,
, 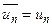
якщо ж 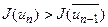 , то покладемо
, то покладемо
 ,
, 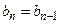 ,
, 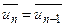 .
.
Новий відрізок 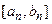 такий, що
такий, що
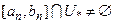 ,
,

точка 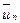 будує золотий перетин відрізка
будує золотий перетин відрізка 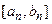 і
і
 .
.
Якщо кількість обчислень значень 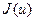 наперед не обмежена, то цей процес можна продовжувати, наприклад, до тієї пори, поки не виконається нерівність
наперед не обмежена, то цей процес можна продовжувати, наприклад, до тієї пори, поки не виконається нерівність 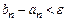 , де
, де 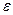 - задана точність. Якщо ж кількість обчислень значень
- задана точність. Якщо ж кількість обчислень значень 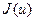 наперед чітко задана і дорівнює n, по процес на цьому закінчується і в якості розв’язку задачі другого типу можна вважати пару
наперед чітко задана і дорівнює n, по процес на цьому закінчується і в якості розв’язку задачі другого типу можна вважати пару 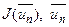 , де
, де 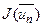 є наближенням для
є наближенням для 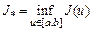 , а також
, а також 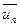 служить наближенням для множини
служить наближенням для множини 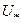 з похибкою
з похибкою
|
|
|
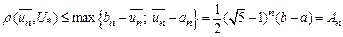 .
.
Розглянемо послідовний метод мінімізації унімодальних функцій на  . Для цього нам знадобляться числа Фібоначчі, які визначаються співвідношеннями
. Для цього нам знадобляться числа Фібоначчі, які визначаються співвідношеннями
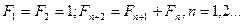 ;
;
Методом математичної індукції легко показати ще n-е число Фібоначчі можна записати в вигляді:
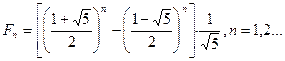 (4)
(4)
Використовуючи числа 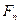 побудуємо n -точковий послідовний метод, який називається методом Фібоначчі. Цей метод відноситься до класу симетричних методів і визначається заданням на відрізку
побудуємо n -точковий послідовний метод, який називається методом Фібоначчі. Цей метод відноситься до класу симетричних методів і визначається заданням на відрізку  симетричних точок
симетричних точок
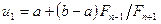 ,
,
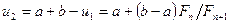 .
.
Методом математичної індукції неважко довести, що коли проведені обчислення значень функції в точках 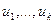 , то мінімум буде локалізовано на відрізку
, то мінімум буде локалізовано на відрізку 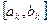 , який має довжину
, який має довжину

причому точка 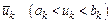 з обчисленним значенням
з обчисленним значенням 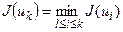 співпадає однією з точок
співпадає однією з точок
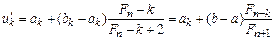
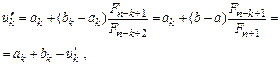 (5)
(5)
які розміщені на відрізку 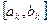 симетрично відносно його середини.
симетрично відносно його середини.
Як видно з (5), при 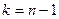 точки
точки 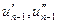 співпадають. Це означає, що при
співпадають. Це означає, що при 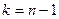 перша частина процесу закінчується обчисленням значення функції в точці
перша частина процесу закінчується обчисленням значення функції в точці  та визначенням відрізка локалізації мінімуму
та визначенням відрізка локалізації мінімуму  довжини
довжини 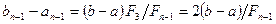 , причому точка
, причому точка 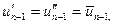 співпадає з серединою відрізка
співпадає з серединою відрізка  ,
,
Наприкінці, порушуючи симетричність процесу, останнє n-е очислення функції 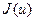 проводиться в точці
проводиться в точці 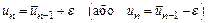 , де
, де  і відрізок локалізації мінімума визначається за формулами
і відрізок локалізації мінімума визначається за формулами 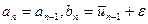 , при
, при 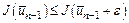 або
або 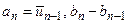 при
при 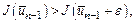 , так що в гіршому випадку
, так що в гіршому випадку 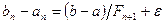 .
.
Цей метод будемо позначати через 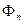 .
.
Мінімізація функцій однієї змінної. (Z=20)
Номер варіанту обчислюється як ((Nсп-1) mod Z) + 1, де Nсп - Ваш номер у журнальному списку.
1. Виберіть функцію з наведеної нижче таблиці, побудуйте її графік засобами MatLab'а (або Excel) в розумному діапазоні для пошуку точок її екстремумів (найбільшого й найменшого значень) із заданою точністю.
2. Для обраної функції знайдіть оптимальне значення методом половинного поділу, методом золотого перетину та методом чисел Фібоначі, попередньо визначивши відрізок локалізації мінімуму. Для кожного методу слід визначити: 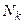 - кількість виконаних ітерацій,
- кількість виконаних ітерацій, 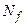 - кількісь обчислень значень цільвої функції,
- кількісь обчислень значень цільвої функції,  -наближене значення точки оптимуму,
-наближене значення точки оптимуму, 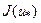 - наближене значення оптимуму цільової функції. Одержані результати подати у вигляді таблиці і порівняти їх:
- наближене значення оптимуму цільової функції. Одержані результати подати у вигляді таблиці і порівняти їх:
|
|
|
| № | Назва методу | 
| 
| ||||||
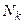
| 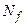
| 
| 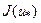
| 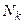
| 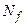
| 
| 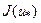
| ||
| Половинного поділу | |||||||||
| Золотого перерізу | |||||||||
| Фібоначчі |
| № | Функція 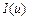
|
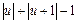
| |
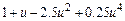
| |
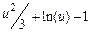
| |
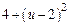
| |
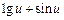
| |
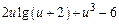
| |
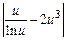
| |
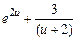
| |
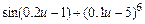
| |
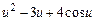
| |
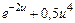
| |
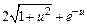
| |
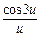
| |

| |
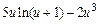
| |
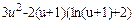
| |
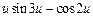
| |
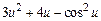
| |
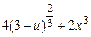
| |

|
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1194; Нарушение авторских прав?; Мы поможем в написании вашей работы!