Парная линейная корреляционная зависимость. Парный линейный коэффициент корреляции, проверка его значимости. Линейное уравнение регрессии

Организаций.

Surrey County Council и удостоен большого количества высоких наград общественных и государственных

Центр предлагает широкий круг спортивных занятий и развлечений в виде обучающих программ. Располагает

прекрасными условиями для проживания в 4-х комнатных домах с душевыми кабинками в каждой комнате, с комнатой отдыха, где можно расслабится и пообщаться и мини-кухней с холодильником, стиральной машиной, посудой.

Питание – полный английский завтрак, горячий обед с большим выбором салатов и полный ужин,

приготовленные на собственной кухне, подаются в кафе на территории центра.

Образовательный цент «High Ashurst» обеспечивает и предоставляет наилучшие условия для творческого

развития, широкий спектр программ личного, социального, эмоционального, физического развития для детей

и подростков, а также дает возможность пообщаться в кругу английских детей, познакомиться с ними и завести

новых друзей. Во время нахождения на территории центра у детей есть уникальная возможность общаться с

английскими преподавателями инструкторами в течении дня.

Признаки Х и Y находятся в корреляционной зависимости, если каждому значению одного признака x_i соответствует определенная условная средняя другого признака.

Парная корреляционная зависимость будет линейной, если она приближенно выражается линейной функцией. Вид зависимости можно определить графически. С этой целью строятся точки с координатами (x_{i ,} ). По расположению построенных точек подбирается линия. Если это будет прямая, то связь линейная.

Целью корреляционного анализа является оценка тесноты связи между признаками. Для этого находится выборочный линейный коэффициент корреляции по формуле

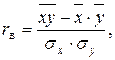
где , , 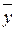– выборочные средние; – выборочные средние квадратические отклонения.

Так как коэффициент корреляции рассчитывается по выборочным данным и является оценкой генерального коэффициента корреляции r _ген , то необходимо проверить значимость . С этой целью выдвигаются нулевая и конкурирующая гипотезы:

Н ₀: r _ген = 0,

Н ₁: r _ген ¹ 0.

Нулевая гипотеза проверяется при заданном уровне значимости a с помощью случайной величины , имеющей распределение Стьюдента с k = n – 2 степенями свободы:

.

По выборочным данным рассчитывают Т _набл, а по таблице критических точек распределения Стьюдента (приложение 5) находим t _{крит.дв}(a, k) с учетом двусторонней критической области. Сравниваем Т _набл и t _{крит.дв}(a, k). Если½ Т _набл½ < t _{крит.дв}(a, k), то есть наблюдаемое значение критерия попало в область принятия гипотезы, то нет оснований отвергать нулевую гипотезу, по данным наблюдения r _ген = 0, r _в незначим, признаки Х и Y некоррелированны. А если Т _набл попало в критическую область, то есть ½ Т _набл½ > t _{крит.дв}(a, k), то нулевую гипотезу отвергаем, справедлива конкурирующая, то есть r _ген ¹ 0, r _в значим, признаки Х и Y коррелированны.

С помощью r _в анализируем тесноту взаимосвязи между признаками X и Y. Чем ближе ½ r _в½ к единице, тем теснее связь между признаками, чем ближе ½ r _в½ к нулю, тем связь слабее.

Далее находим коэффициент детерминации по формуле D = × 100 %, который показывает, на сколько процентов в среднем вариация результативного признака Y объясняется за счет вариации факторного признака X.

Следующим этапом является регрессионный анализ, с помощью которого корреляционную зависимость между признаками приближенно выражаем в виде линейного уравнения регрессии вида » a ₀ + a ₁ . Неизвестные параметры a ₀ и a ₁ находятся методом наименьших квадратов. Применяя этот метод, получаем следующую систему нормальных уравнений:

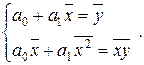
Решая систему, находим оценки параметров a ₀ и a ₁. Уравнение регрессии можно записать в таком виде: – = a ₁(x – ), где .

Параметр a ₁ – коэффициент регрессии – показывает, как изменится в среднем результативный признак, если факторный признак увеличится на единицу своего измерения. Уравнение регрессии можно использовать для прогнозирования (предсказания).

Пример 11. Изучается зависимость себестоимости одного изделия (Y, р.) от величины выпуска продукции (Х, тыс. шт.) по группе предприятий за отчетный период. Получены следующие данные:

	Х
	Y	1,9	1,7	1,8	1,6	1,4.

Провести корреляционно-регрессионный анализ зависимости себестоимости одного изделия от выпуска продукции.

Решение. Признак Х – объем выпускаемой продукции, тыс. шт. (факторный признак). Признак Y – себестоимость одного изделия, р. (результативный признак). Предполагаем, что признаки имеют нормальный закон распределения. Признаки находятся в статистической зависимости, так как себестоимость одного изделия зависит не только от объема выпускаемой продукции, но и от многих других факторов, которые в данном случае не учитываются. Определим форму связи. Построим точки с координатами (х_i, y_i) и по их расположению определим форму связи (рис. 6).

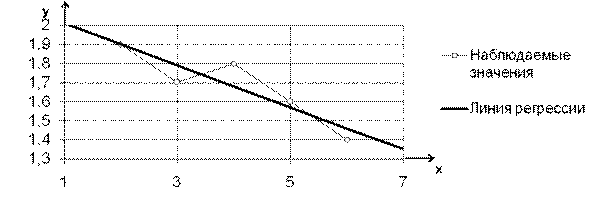
Рис. 6

Итак, форма связи линейная.

Проведем корреляционный анализ. Рассчитаем выборочный линейный коэффициент корреляции:

Расчеты представим в таблице:

	хi	yi	хi × yi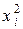
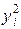
		1,9 1,7 1,8 1,6 1,4	3,8 5,1 7,2 8,0 8,4		3,61 2,89 3,24 2,56 1,96
Итого		8,4	32,5		14,26.

Проверим значимость выборочного коэффициента корреляции. Для этого выдвигаем гипотезы:

Н ₀: r _ген = 0,

Н ₁: r _ген ¹ 0. Примем уровень значимости .

Для проверки нулевой гипотезы используем случайную величину , имеющую распределение Стьюдента с k = n – 2 = 3 степенями свободы. По выборочным данным находим наблюдаемое значение критерия Т _набл = » – 3,58. По таблице критических точек распределения Стьюдента (приложение 5) находим t _{крит.дв}(0,05; 3) = 3,18. Сравниваем Т _набл и t _крит(0,05; 3). Так как ½ Т _набл½ > t _{крит.дв}(0,05; 3), то есть Т _набл попало в критическую область, нулевая гипотеза отвергается, справедлива конкурирующая гипотеза: r _ген ¹ 0, r _в значим. Признаки Х и Y коррелированны. Так как ½ r _в½ близок к единице, следовательно, себестоимость одного изделия и объем выпускаемой продукции находятся в тесной корреляционной зависимости.

Найдем коэффициент детерминации. D = r _в² × 100 % = 0,81 %, то есть вариация себестоимости единицы продукции в среднем на 81 % объясняется вариацией объема выпускаемой продукции.

Выразим эту связь аналитически приблизительно в виде линейного уравнения регрессии:

– » a ₁(х – ),

.

– 1,68 = – 0,11 (x – 4) или » – 0,11 x + 2,12.

Из уравнения следует, что с увеличением выпуска продукции на 1 тыс. шт. себестоимость одного изделия снизится в среднем на 0,11 р.

Найдем по уравнению регрессии себестоимость одного изделия, если выпуск продукции составит 5,2 тыс. шт.:

» – 0,11 × 5,2 + 2,12 = 1,55 (р.)

Пример 12. Для нормирования труда проведено статистическое исследование связи между количеством изготавливаемых изделий (Х, шт.) и затратами времени на обработку одного изделия (Y, мин). Сделана выборка объемом n = 51 и получены следующие данные: r _в = 0,8, = 8, s_x = 3,2, 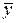= 40, s_y = 8. Проверить значимость коэффициента корреляции при a = 0,02. Построить уравнение регрессии.

Решение. Признак Х – количество изготавливаемых изделий, шт. Признак Y – затраты времени на обработку одного изделия, мин.

Предполагаем, что признаки имеют нормальный закон распределения. Они находятся в статистической зависимости, так как затраты времени зависят не только от количества изготавливаемых изделий, но и от многих других факторов, которые в данном случае не учитываются. В данном случае связь линейная, теснота связи характеризуется линейным коэффициентом корреляции r _в = 0,8. Но прежде чем делать вывод о тесноте взаимосвязи, необходимо проверить значимость коэффициента корреляции. Выдвигаем нулевую гипотезу и ей конкурирующую:

Н ₀: r _ген = 0,

Н ₁: r _ген ¹ 0.

Проверяем нулевую гипотезу с помощью случайной величины, имеющей распределение Стьюдента с k = n – 2 = 49 степенями свободы: .

По выборочным данным найдем наблюдаемое значение критерия Т _набл = » 9,33. По таблице критических точек распределения Стьюдента (приложение 5) находим t _{крит.дв}(a, k) = t _{крит.дв}(0,02; 49) = 2,40. Сравниваем Т _набл и t _{крит.дв}(0,02; 49). Так как½ Т _набл½ > t _{крит.дв}(0,02; 49), то есть наблюдаемое значение критерия попало в критическую область, нулевая гипотеза отвергается, справедлива конкурирующая гипотеза: r _ген ¹ 0, признаки Х и Y коррелированны, r _в значим.

D = × 100 % = 64 %, то есть вариация затрат времени на обработку одного изделия в среднем на 64 % объясняется за счет вариации количества изготавливаемых изделий.

Выразим эту взаимосвязь аналитически в виде уравнения регрессии вида:

– » a ₁(х – ).

Коэффициент a ₁ выразим через парный линейный коэффициент кор­реляции:

;

Сравнивая эти две формулы, можем записать:

Тогда по выборочным данным будем иметь:

a ₁ = 0,8 × 8/32 = 2; – 40» 2(x – 8) или » 24 + 2 x.

Из уравнения следует, что с увеличением количества выпускаемых изделий на 1 шт., затраченное время в среднем увеличится на 2 мин.

Дата добавления: 2015-07-02