
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Непрерывность функции
|
|
|
|
Замечательные пределы.
Сравнение бесконечно малых
пусть 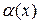 и
и  - бесконечно малые функции при
- бесконечно малые функции при  (
( ) и существует предел
) и существует предел 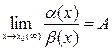 , тогда:
, тогда:
1) если 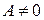 , то
, то 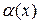 и
и  называются бесконечно малыми одного порядка;
называются бесконечно малыми одного порядка;
2) если  , то
, то 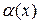 и
и  называются эквивалентными бесконечно малыми (
называются эквивалентными бесконечно малыми ( );
);
3) если 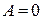 , то
, то 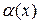 - бесконечно малая более высокого порядка по сравнению с
- бесконечно малая более высокого порядка по сравнению с  .
.
Например, при 
 ,
,  ,
,  ,
, 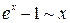 .
.
Теорема. Предел отношения двух бесконечно малых равен пределу отношения бесконечно малых, эквивалентных данным, т.е. если 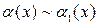 ,
, 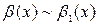 при
при  (
( ), то
), то  .
.
Первым замечательным пределом называется предел вида  .
.
Следствие. 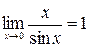
Вторым замечательным пределом называется предел: 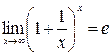 .
.
Следствие.  (число
(число  ).
).
Пример. Вычислить пределы:
а) 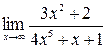 ;
б) ;
б) 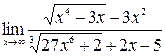 ;
в) ;
в) 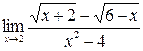 ; ;
| г) 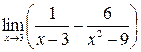 ;
д) ;
д) 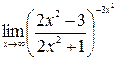 ; ;
| е) 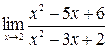 ;
ж) ;
ж) 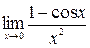 . .
|
Решение:
а)  .
.
б) 
 .
.
в) 

 .
.
г) 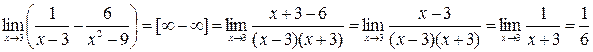 .
.
д) 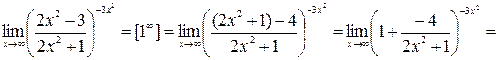
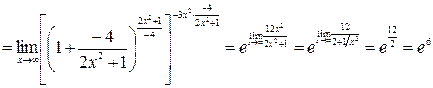 .
.
е) 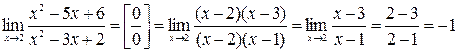 .
.
ж) 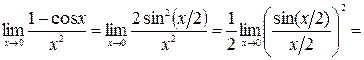
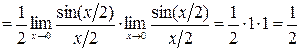 .
.
Функция  называется непрерывной в точке
называется непрерывной в точке  , если она удовлетворяет следующим условиям: 1) определена в точке
, если она удовлетворяет следующим условиям: 1) определена в точке  , т.е. существует
, т.е. существует 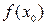 ; 2) имеет конечные односторонние пределы функции при
; 2) имеет конечные односторонние пределы функции при  слева и справа; 3) эти пределы равны значению функции в точке
слева и справа; 3) эти пределы равны значению функции в точке  , т.е.
, т.е. 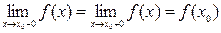 .
.
Пример. Исследовать функции на непрерывность в точке 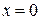 : а)
: а)  , б)
, б) 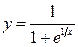 .
.
Решение: а)  . При
. При 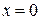 функция определена,
функция определена, 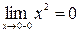 ,
, 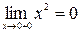 ,
,  , т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция
, т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция  в точке
в точке 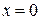 непрерывна.
непрерывна.
б) 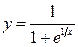 . При
. При 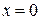 функция не определена;
функция не определена; 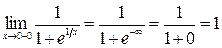 ;
;  . Т.о. в точке
. Т.о. в точке 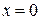 функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.
функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.
Функция  называется непрерывной в точке
называется непрерывной в точке  , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:  .
.
Точка  называется точкой разрыва функции
называется точкой разрыва функции  , если эта функция в данной точке не является непрерывной. Различают точки разрыва:
, если эта функция в данной точке не является непрерывной. Различают точки разрыва:
Первого рода – когда существуют конечные односторонние пределы функции слева и справа при  , не равные друг другу:
, не равные друг другу: 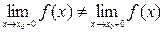 . К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при
. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при  существует, но не равен значению функции в этой точке.
существует, но не равен значению функции в этой точке.
|
|
|
Второго рода – когда хотя бы один из односторонних пределов слева 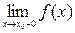 или справа
или справа 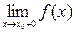 равен бесконечности или не существует.
равен бесконечности или не существует.
Свойства функций, непрерывных в точке:
1. Если функции  и
и 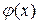 непрерывны в точке
непрерывны в точке  , то их сумма
, то их сумма  , произведение
, произведение  и частное
и частное  (при условии
(при условии 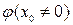 ) являются функциями, непрерывными в точке
) являются функциями, непрерывными в точке  .
.
2. Если функция  непрерывна в точке
непрерывна в точке  и
и  , то существует такая окрестность точки
, то существует такая окрестность точки  , в которой
, в которой  .
.
3. Если функция  непрерывна в точке
непрерывна в точке 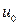 , а функция
, а функция 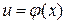 непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция  непрерывна в точке
непрерывна в точке  . Свойство можно записать:
. Свойство можно записать: 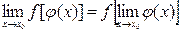 , т.е. под знаком непрерывной функции можно переходить к пределу.
, т.е. под знаком непрерывной функции можно переходить к пределу.
Функция  называется непрерывнойна промежутке
называется непрерывнойна промежутке 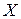 , если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.
, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.
Свойства функций, непрерывных на отрезке:
1. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
2. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она достигает на этом отрезке наименьшего значения
, то она достигает на этом отрезке наименьшего значения 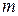 и наибольшего значения
и наибольшего значения 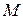 (теорема Вейерштрасса).
(теорема Вейерштрасса).
3. Если функция  непрерывна на отрезке
непрерывна на отрезке  и значения ее на концах отрезка
и значения ее на концах отрезка 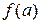 и
и  имеют противоположные знаки, то внутри отрезка найдется точка
имеют противоположные знаки, то внутри отрезка найдется точка  такая, что
такая, что 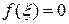 . (Теорема Больцано-Коши.)
. (Теорема Больцано-Коши.)
Пример. Исследовать на непрерывность и найти точки разрыва функции  . Установить характер разрыва.
. Установить характер разрыва.
Решение: При 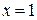 функция не определена, следовательно, функция в точке
функция не определена, следовательно, функция в точке 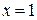 терпит разрыв:
терпит разрыв:  , а
, а  . Так как односторонние пределы бесконечны, то
. Так как односторонние пределы бесконечны, то 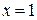 - точка разрыва второго рода.
- точка разрыва второго рода.
Задания для самостоятельной работы.
Вычислить пределы:
1. 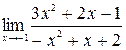 .
2. .
2. 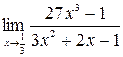 .
3. .
3. 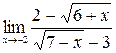 .
4. .
4.  .
5. .
5.  .
6. .
6. 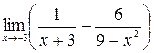 .
7. .
7. 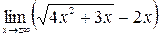 .
8. .
8. 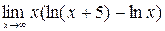 . .
| 9. 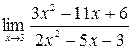 .
10. .
10.  .
11. .
11. 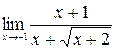 .
12. .
12.  .
13. .
13. 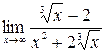 .
14. .
14. 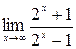 .
15. .
15. 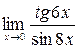 .
16. .
16.  . .
| 17. 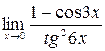 .
18. .
18. 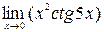 .
19. .
19.  .
20. .
20. 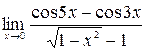 .
21. .
21.  .
22. .
22.  .
23. .
23. 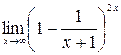 .
24. .
24. 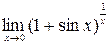 . .
|
Вычислить односторонние пределы:
|
|
|
25. 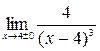 . .
| 26. 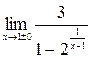 . .
| 27.  . .
|
Найти точки разрыва и построить графики функций:
28.  .
29. .
29. 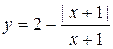 .
30. .
30.  . .
| 31. 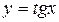 .
32. .
32.  .
33. .
33.  . .
| 34.  .
35. .
35. 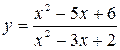 . .
|
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 430; Нарушение авторских прав?; Мы поможем в написании вашей работы!