Сравнение бесконечно малых функций

ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ

ЗАМЕЧАНИЕ

Неопределнность единица в степени бесконечность является степенной

Сравнение функций

при если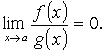

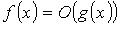при если существуют интеграл содержащий точку a, и постоянная M, такие, что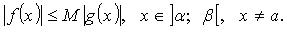

Локально эквивалентные функции: при если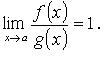

Некоторые эквивалентности (при ):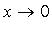

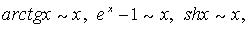
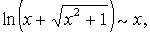
Формула Стирлинга: при

Числовые ряды

Частная (частичная) сумма ряда:

Сумма ряда: 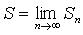(если предел существует).

Ряд сходится, если S конечно; тогда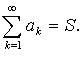

Необходимое условие сходимости ряда:

Остаток ряда:

Гармонический ряд расходится; его частная сумма

(C - постоянная Эйлера: C = 0,5772...; ).

Обобщенный гармонический ряд сходится при 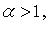расходится при

Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.

Две б.м.ф. сравниваются между собой с помощью их отношения.

Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→х_о, т. е.

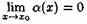и

1. Если 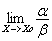=А¹ 0 (АєR), то α и ß называются бесконечно малыми одного порядка.

2. Если, 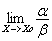=0, то α називатся бесконечно малой более высокого порядка, чем ß.

3. Если 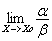=∞, то α называется бесконечно малой более низкого порядка, чем ß.

4. Если 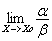не существует, то α и ß называются несравнимыми бесконечно малыми.

Отметим, что таковы же правила сравнения б.м.ф. при х →±∞, х →х₀±0.

<< Пример 18.1<

Сравнить порядок функций α=3х² и ß=14х² при х→0

Решение: При х→0 это б.м.ф. одного порядка, так как

Говорят, что б.м.ф. а и ß одного порядка стремятся к нулю с примерно одинаковой скоростью

<< Пример 18.2

Являются ли функции α=3х⁴ и ß=7х б.м.ф. одного порядка при х→0?

Решение: При х→0 функция α есть б.м.ф. более высокого порядка, чем ß, так как

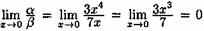
В этом случае б.м.ф. α стремится к нулю быстрее, чем ß.

<< Пример 18.3

Сравнить порядок функций α=tgx и ß=х² при х→0.

Решение: Так как

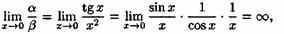
то α есть б.м.ф. более низкого порядка, чем ß.

<< Пример 18.4

Можно ли сравнить функции 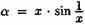и ß=х при х→0?

Решение: Функции 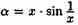и ß=х при х→0 являются несравнимыми б.м.ф., так как предел

не существует.

Дата добавления: 2015-07-02