
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разложение в ряд Фурье непериодических функций
Ряд Фурье для функций с периодом 2l.
Пусть функция f(x) задана в симметричном промежутке [-l, l] произвольной длины 2 l > 0. Если использовать подстановку x = ly/  , где -
, где -  < y <
< y <  , то получаем функцию f(ly/
, то получаем функцию f(ly/  ) от аргумента у в промежутке [-
) от аргумента у в промежутке [-  ,
,  ] и ее можно разложить в ряд Фурье по переменной у: f(ly/
] и ее можно разложить в ряд Фурье по переменной у: f(ly/  ) = a0/2 +
) = a0/2 + 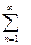 ancos nу + bnsin nу
ancos nу + bnsin nу
а0 = 1/ 
 ; an = 1/
; an = 1/ 
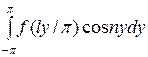 ; bn = 1/
; bn = 1/ 
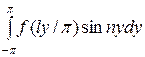
Теперь вернемся к прежней переменной x, используя обратное преобразование y =  x/l, тогда
x/l, тогда
f(x) = a0/2 + 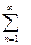 ancos n
ancos n  x/l + bnsin n
x/l + bnsin n  x/l (26)
x/l (26)
а0 = 1/ l  ; an = 1/ l
; an = 1/ l 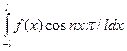 ; bn = 1/ l
; bn = 1/ l  (27)
(27)
Эти формулы определяют разложение в ряд Фурье функции с периодом произвольной длины.
Пр. Разложить в ряд Фурье функцию с периодом 2 l = 2, заданную формулой
f(x) = x, x 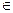 [-1, 1]
[-1, 1]
Решение. Функция удовлетворяет условиям Дирихле, нечетная, поэтому an = 0,
bn = 1/ l  = 2
= 2  = (-2/
= (-2/  n)x cos n
n)x cos n  x|01 + (2/
x|01 + (2/  n)
n) 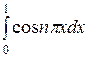 =
=
= (-2/  n)x cos n
n)x cos n  = 2(-1)n+1/ n
= 2(-1)n+1/ n 
В точках непрерывности f(x) = 2/ 
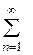 (-1)n+1/ n sin
(-1)n+1/ n sin  x, а в точках разрыва равна 0.
x, а в точках разрыва равна 0.
В ряд Фурье можно разлагать не только периодические функции, но и любые ограниченные функции, определенные на конечном участке числовой оси, если вне этого участка поведение функции нас не интересует. Если участок оси симметричен [-l, l], то используется разложение (26), (27). Если функция f(x) задана на сегменте [0, l], то для разложения в ряд Фурье достаточно доопределить ее в сегменте [-l, 0] произвольным образом, а затем разложить в ряд Фурье, считая ее заданной в сегменте [-l, l]. Наиболее удобно доопределять функцию условием четности f(-x) = f(x) или нечетности f(-x) = -f(x). В этом случае используются разложение только по синусам или только по косинусам в формулах (26), (27).
Пр. Разложить в ряд Фурье функцию заданную в сегменте [0, 1] уравнением f(x) = x
Решение 1. Доопределим функцию f(x) на сегменте [-1, 0] нечетным образом, т.е. f(x) = x на сегменте [-1, 1]. В этом случае приходим к рассмотренной выше задаче
f(x) = 2/ 
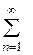 [(-1)n+1 sin
[(-1)n+1 sin  n x] /n
n x] /n
Решение 2. Доопределим функцию f(x) на сегменте [-1, 0] четным образом, т.е. f(x) = -x. В этом случае bn = 0, а0 = 1/ l 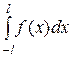 = 2
= 2 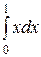 = 1;
= 1;
an = 1/ l 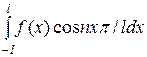 = 2
= 2  = - (2/
= - (2/  2 )(1 - cos
2 )(1 - cos  n)/n2 =
n)/n2 =
= - (2/  2n2 ) (1 – (-1)n) = - (2/
2n2 ) (1 – (-1)n) = - (2/  2n2 ) {
2n2 ) { 
или а2m = 0, a2m+1 = - 4/  2 (2m+1)2, т.е. получаем разложение f(x) по нечетным гармоникам косинуса f(x) = - 4/
2 (2m+1)2, т.е. получаем разложение f(x) по нечетным гармоникам косинуса f(x) = - 4/  2
2 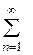 cos
cos  (2m+1)x / (2m+1)2
(2m+1)x / (2m+1)2
Оба решения на сегменте [0, 1] дают одинаковыйчисленный и графический результат, а за его пределами значения функций различны.
. Собственные и несобственные интегралы, зависящие от параметра. Равномерная сходимость. Непрерывность и дифференцируемость несобственных интегралов. Эйлеровы интегралы.
Рассмотрим функцию f(x,y) двух переменных, определенную для всех значений х в некотором промежутке [а, b] и всех значений у. Пусть, при каждом постоянном значении у будет интегрируема в промежутке [а, b], в собственном или в несобственном смысле. Тогда интеграл
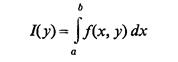
будет, очевидно, функцией от вспомогательной переменной или параметра у.
При изучении свойств функции, которая задана интегралом, содержащим параметр у,
важное значение имеет вопрос о производной этой функции по параметру.


Поставим, наконец, вопрос об интеграле по у, скажем, в промежутке [с, д].
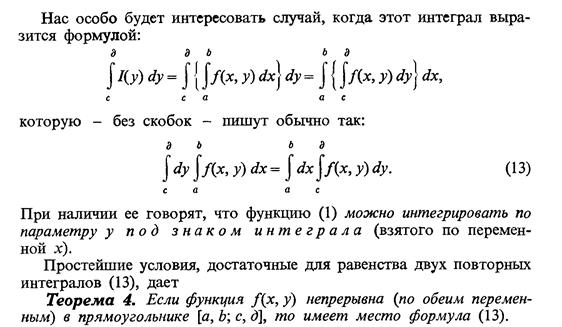
|
|
Дата добавления: 2015-07-02; Просмотров: 836; Нарушение авторских прав?; Мы поможем в написании вашей работы!