
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Фурье решения смешанной задачи
|
|
|
|
Исследуем решение простейших уравнений гиперболического и параболического типов.
А) Рассмотрим задачу решения волнового уравнения
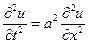 (
(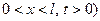 (5.1)
(5.1)
с граничными условиями
 (5.2)
(5.2)
при начальных условиях
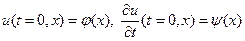 (
(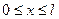 ), (5.3)
), (5.3)
где 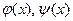 - непрерывные функции, заданные на промежутке
- непрерывные функции, заданные на промежутке  . Задача нахождения решения уравнения (5.1), удовлетворяющее указанным начальным и граничным условиям, называется смешанной задачей для волнового уравнения (5.1).
. Задача нахождения решения уравнения (5.1), удовлетворяющее указанным начальным и граничным условиям, называется смешанной задачей для волнового уравнения (5.1).
Будем искать решение 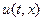 уравнения (5.1) с помощью метода разделения переменных, т.е. строим решение в виде
уравнения (5.1) с помощью метода разделения переменных, т.е. строим решение в виде
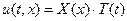 , (5.4)
, (5.4)
где функция 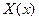 зависит от одной переменной x, а функция
зависит от одной переменной x, а функция  - зависит только от переменной t.
- зависит только от переменной t.
Подставляя в уравнение (5.1) решение, записанное в виде (5.4), получим равенство:
 .
.
Разделяем в полученном равенстве переменные (с учетом того, что ищем не тождественно равное нулю решение):
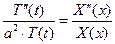 . (5.5)
. (5.5)
Поскольку при подстановке решения в исходное уравнение полученное равенство должно выполняться при всех значениях переменных x, t, то равенство (5.5) возможно тогда и только тогда, когда обе части его равны одной и той же постоянной, которую обозначим (‒λ). После приравнивания обеих частей равенства (5.5) указанной константе, получим систему обыкновенных дифференциальных уравнений:

Запишем граничные условия (5.2) в терминах новых искомых функций 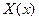 и
и  :
:
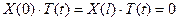 .
.
Поскольку  при всех t, то граничные условия для функции
при всех t, то граничные условия для функции 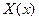 примут вид:
примут вид:
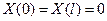 .
.
В итоге получаем задачу Штурма-Лиувилля:
 (5.8)
(5.8)
Решением задачи (5.8) являются собственные числа 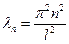 (
(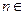 ℕ), каждому из которых соответствует собственная функция
ℕ), каждому из которых соответствует собственная функция
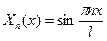 (5.9)
(5.9)
Подставляя найденные числа 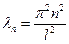 в уравнение (5.7), получим линейной однородное дифференциальное уравнение для нахождения функций
в уравнение (5.7), получим линейной однородное дифференциальное уравнение для нахождения функций  :
: 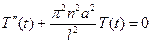 , решая которое методом Эйлера, находим
, решая которое методом Эйлера, находим
|
|
|
 . (5.10)
. (5.10)
В итоге частные решения уравнения (5.1) принимают вид  .
.
Идея метода Фурье состоит в том, что общее решение задачи (5.1) ищется в виде суммы частных решений 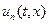 :
:
 . (5.11)
. (5.11)
Чтобы окончательно найти решение 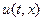 остается лишь доопределить коэффициенты
остается лишь доопределить коэффициенты 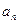 и
и 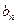 функции
функции  так, чтобы решение (5.11) удовлетворяло начальным условиям (5.3). Предварительно вычислив частную производную
так, чтобы решение (5.11) удовлетворяло начальным условиям (5.3). Предварительно вычислив частную производную 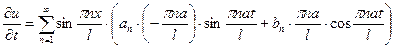 и подставив в
и подставив в 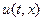 и в
и в 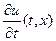
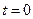 , с учетом (5.3) получаем:
, с учетом (5.3) получаем:
 (5.12)
(5.12)
Формулы (5.12) представляют собой разложения функций 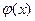 и
и  в ряд Фурье по синусам в интервале
в ряд Фурье по синусам в интервале  , т.е.
, т.е.
 (5.13)
(5.13)
Подставляя найденные по формулам (5.13) коэффициенты 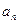 и
и 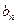 в выражение (5.11), получаем общее решение смешанной задачи для волнового уравнения.
в выражение (5.11), получаем общее решение смешанной задачи для волнового уравнения.
Пример 1. Решить задачу о свободных колебаниях конечной однородной струны, закрепленной на концах 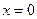 и
и 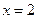 , если начальное отклонение струны имеет форму параболы с уравнением
, если начальное отклонение струны имеет форму параболы с уравнением  , а начальная скорость точек струны равна нулю (коэффициент a считать равным 9).
, а начальная скорость точек струны равна нулю (коэффициент a считать равным 9).
Решение: пусть 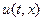 - искомая функция, описывающая отклонение струны от положения равновесия в точке с координатой x в момент времени t. Тогда эта функция удовлетворяет волновому уравнению (5.1), с граничными условиями (5.2) (которые выражают закрепленность концов струны) и начальными условиями (5.3) (которые выражают начальную форму и начальную скорость точек струны), где
- искомая функция, описывающая отклонение струны от положения равновесия в точке с координатой x в момент времени t. Тогда эта функция удовлетворяет волновому уравнению (5.1), с граничными условиями (5.2) (которые выражают закрепленность концов струны) и начальными условиями (5.3) (которые выражают начальную форму и начальную скорость точек струны), где 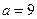 ,
, 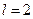 ,
,  ,
,  .
.
Используя формулу (11), получим, что решение данной задачи имеет вид
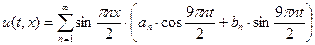 . (5.14)
. (5.14)
Для нахождения 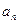 и
и 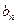 воспользуемся системой (5.12):
воспользуемся системой (5.12):
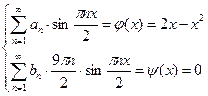 .
.
Следовательно, используя (5.13), получим:
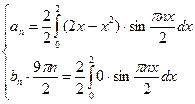 (n ∈ℕ),
(n ∈ℕ),
откуда следует, что 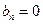 , а для нахождения коэффициентов
, а для нахождения коэффициентов 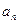 необходимо вычислить интегралы:
необходимо вычислить интегралы:
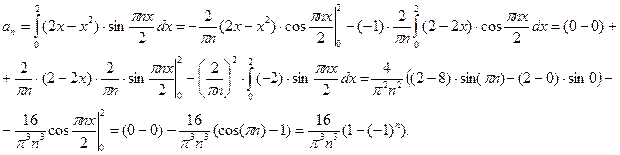
Подставляя найденные коэффициенты в (5.14), получаем решение
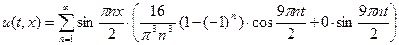 .
.
Ответ:  .
.
Пример 2. Для струны, закрепленной на концах 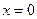 и
и 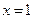 , найти решение волнового уравнения
, найти решение волнового уравнения
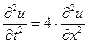 ,
,
удовлетворяющее начальным условиям:
 ;
;
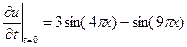 .
.
Решение: по условию задачи: 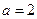 ,
, 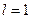 ,
,  ,
, 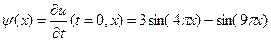 . С учетом формулы (5.11) решение указанной смешанной задачи примет вид:
. С учетом формулы (5.11) решение указанной смешанной задачи примет вид:
|
|
|
 . (5.15)
. (5.15)
Поэтому из (5.13) получим систему:
 (5.16)
(5.16)
Поскольку система собственных функций  обладает свойством ортогональности, то
обладает свойством ортогональности, то
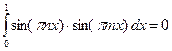 , если
, если 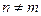 . (5.17)
. (5.17)
Поэтому 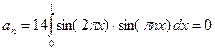 для всех натуральных чисел
для всех натуральных чисел 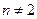 .
.
При 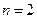 получаем:
получаем:
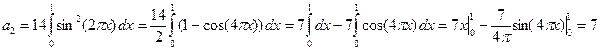 .
.
Аналогично определяем:
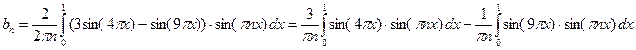 .
.
Учитывая свойство ортогональности (5.17), заметим, что
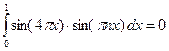 для всех
для всех 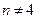
и
 для всех
для всех  .
.
Следовательно, все коэффициенты 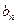 (n ∈ℕ), кроме
(n ∈ℕ), кроме  и
и 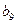 , равны нулю.
, равны нулю.
При  имеем:
имеем:
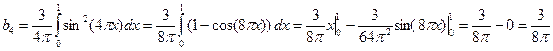 .
.
При  :
:
 .
.
Подставляя найденные коэффициенты в (5.15), получим
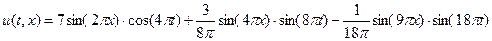 .
.
Ответ: 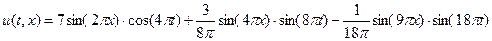 .
.
Б) Рассмотрим задачу решения уравнения теплопроводности
 (
(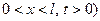 (5.18)
(5.18)
с граничными условиями
 (5.19)
(5.19)
при начальном условии
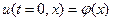 (
(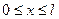 ), (5.20)
), (5.20)
где 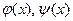 - непрерывные функции, заданные на промежутке
- непрерывные функции, заданные на промежутке  . Задача нахождения решения уравнения (5.18), удовлетворяющее указанным начальным и граничным условиям (5.19) и (5.20), называется смешанной задачей для уравнения теплопроводности (5.18).
. Задача нахождения решения уравнения (5.18), удовлетворяющее указанным начальным и граничным условиям (5.19) и (5.20), называется смешанной задачей для уравнения теплопроводности (5.18).
Будем искать решение 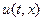 уравнения (5.18) с помощью метода разделения переменных, т.е. строим решение в виде
уравнения (5.18) с помощью метода разделения переменных, т.е. строим решение в виде
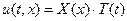 , (5.21)
, (5.21)
где функция 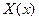 зависит от одной переменной x, а функция
зависит от одной переменной x, а функция  - зависит только от переменной t.
- зависит только от переменной t.
Подставляя в уравнение (5.18) решение, записанное в виде (5.21), получим равенство:
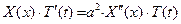 .
.
Разделяем в полученном равенстве переменные (с учетом того, что ищем не тождественно равное нулю решение):
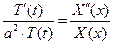 . (5.22)
. (5.22)
Поскольку при подстановке решения в исходное уравнение полученное равенство должно выполняться при всех значениях переменных x, t, то равенство (5.22) возможно тогда и только тогда, когда обе части его равны одной и той же постоянной, которую обозначим (‒λ). После приравнивания обеих частей равенства (5.22) указанной константе, получим систему обыкновенных дифференциальных уравнений:

Запишем граничные условия (5.19) в терминах новых искомых функций 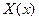 и
и  :
:
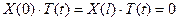 .
.
Поскольку  при всех t, то граничные условия для функции
при всех t, то граничные условия для функции 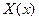 примут вид:
примут вид:
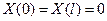 .
.
В итоге получаем задачу Штурма-Лиувилля:
 (5.25)
(5.25)
Решением задачи (5.25) являются собственные числа 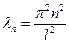 (
(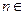 ℕ), каждому из которых соответствует собственная функция
ℕ), каждому из которых соответствует собственная функция
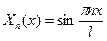 . (5.26)
. (5.26)
Подставляя найденные числа 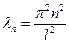 в уравнение (5.24), получим линейной однородное дифференциальное уравнение для нахождения функций
в уравнение (5.24), получим линейной однородное дифференциальное уравнение для нахождения функций  :
:  , решая которое путем разделения переменных, находим
, решая которое путем разделения переменных, находим
 . (5.27)
. (5.27)
В итоге частные решения уравнения (5.18) принимают вид  .
.
Идея метода Фурье состоит в том, что общее решение задачи (5.18) ищется в виде суммы частных решений 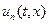 :
:
|
|
|
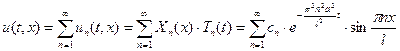 . (5.28)
. (5.28)
Чтобы окончательно найти решение 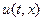 остается лишь доопределить коэффициенты
остается лишь доопределить коэффициенты 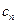 функции
функции  так, чтобы решение (5.28) удовлетворяло начальному условию (5.20). Подставив в
так, чтобы решение (5.28) удовлетворяло начальному условию (5.20). Подставив в 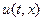 значение
значение 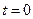 , с учетом (5.20) получаем:
, с учетом (5.20) получаем:
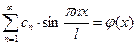 (5.29)
(5.29)
Формула (5.29) представляет собой разложение функции 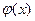 в ряд Фурье по синусам в интервале
в ряд Фурье по синусам в интервале  , т.е.
, т.е.
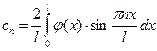 , (
, (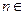 ℕ) (5.30)
ℕ) (5.30)
Подставляя найденные по формулам (5.20) коэффициенты 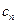 в выражение (5.28), получаем общее решение смешанной задачи для уравнения теплопроводности.
в выражение (5.28), получаем общее решение смешанной задачи для уравнения теплопроводности.
Замечание. Существуют методы решения неоднородного уравнения теплопроводности  и с ненулевыми краевыми условиями
и с ненулевыми краевыми условиями 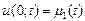 ,
, 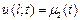 , они также основаны на рассмотренном методе Фурье (методе разделения переменных). Эти приемы здесь рассматривать не будем.
, они также основаны на рассмотренном методе Фурье (методе разделения переменных). Эти приемы здесь рассматривать не будем.
Пример 3. Найти функцию, определяющую распределение температуры внутри стержня длины 5, на концах которого поддерживается нулевая температура, а начальная температура стержня задана функцией  (коэффициент a считать равным 2).
(коэффициент a считать равным 2).
Решение: пусть 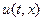 - искомая функция, описывающая распределение температуры внутри стержня в точке с координатой x в момент времени t. Тогда эта функция удовлетворяет уравнению теплопроводности (5.18), с граничными условиями (5.19), выражающими тот факт, что на концах стержня
- искомая функция, описывающая распределение температуры внутри стержня в точке с координатой x в момент времени t. Тогда эта функция удовлетворяет уравнению теплопроводности (5.18), с граничными условиями (5.19), выражающими тот факт, что на концах стержня 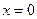 и
и  , и начальным условием (5.20), определяющим начальную температуру стержня, где
, и начальным условием (5.20), определяющим начальную температуру стержня, где 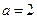 ,
, 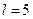 ,
, 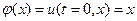 .
.
Используя формулу (28), получим, что решение данной задачи имеет вид
 (5.31)
(5.31)
Для нахождения 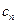 воспользуемся формулами (5.30):
воспользуемся формулами (5.30):
 (n ∈ℕ),
(n ∈ℕ),
откуда:

Подставляя найденные коэффициенты в (5.31), получаем решение
 .
.
Ответ: 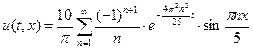 .
.
Замечание. В зависимости от задач граничные условия ((5.2), (5.19)) могут иметь другой вид, нежели тот, который описан в пунктах А) и Б), в этом случае собственные числа и собственные функции ((5.9), (5.26)) соответствующих задач Штурма-Лиувилля ((5.8), (5.25)) будут определяться иначе, а именно:
а) если граничные условия принимают вид  , то соответствующая задача Штурма-Лиувилля будет иметь решение
, то соответствующая задача Штурма-Лиувилля будет иметь решение 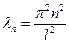 ,
,  , n ∈ℕ∪{0};
, n ∈ℕ∪{0};
б) если граничные условия принимают вид  , то соответствующая задача Штурма-Лиувилля будет иметь решение
, то соответствующая задача Штурма-Лиувилля будет иметь решение  ,
, 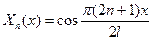 , n ∈ℕ∪{0};
, n ∈ℕ∪{0};
|
|
|
в) если граничные условия принимают вид  , то соответствующая задача Штурма-Лиувилля будет иметь решение
, то соответствующая задача Штурма-Лиувилля будет иметь решение  ,
,  , n ∈ℕ∪{0}.
, n ∈ℕ∪{0}.
Граничные условия вида а) в случае волновых уравнений интерпретируются как подвижность обоих концов струны, а условия б) и в) означают то, что один конец струны закреплен, а другой – нет. Для уравнений теплопроводности условия типа а) означают теплоизолированность концов стержня от окружающей среды, а условия типа б) и в) означают то, что один конец стержня теплоизолирован, а другой поддерживается при нулевой температуре.
В связи с указанными изменениями общее решение соответствующих смешанных задач примет другой вид по сравнению с тем, который описан в пунктах А) и Б).
Задачи для самостоятельного решения:
1. Найти закон свободных колебаний струны, закрепленной на концах 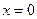 и
и 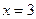 , если в начальный момент времени форма струны имеет вид ломаной OAB, где O (0; 0), A (2; -0,1), B (3; 0). Найти форму струны в момент времени t, если начальные скорости точек равны нулю.
, если в начальный момент времени форма струны имеет вид ломаной OAB, где O (0; 0), A (2; -0,1), B (3; 0). Найти форму струны в момент времени t, если начальные скорости точек равны нулю.
Ответ: 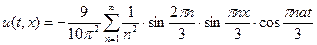 .
.
2. Найти закон свободных колебаний (в случае  ) струны длины 1, расположенной на отрезке
) струны длины 1, расположенной на отрезке 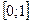 , если в начальный момент времени струне придали форму параболы
, если в начальный момент времени струне придали форму параболы
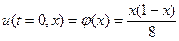 ,
,
а затем струну отпустили с начальной скоростью, равной нулю.
Ответ:  .
.
3. В полуполосе  ,
, 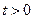 для уравнения
для уравнения
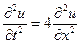
решить смешанную задачу:
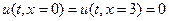 ,
,
 .
.
Ответ:  .
.
4. Найти закон распределения температуры  внутри стержня, у которого левый конец (при
внутри стержня, у которого левый конец (при 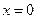 ) поддерживают при постоянной нулевой температуре, а правый конец (при
) поддерживают при постоянной нулевой температуре, а правый конец (при 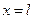 ) теплоизолирован от окружающей среды, т.е.
) теплоизолирован от окружающей среды, т.е. 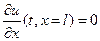 . Причем начальная температура стержня задана функцией
. Причем начальная температура стержня задана функцией
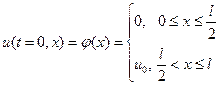 .
.
Ответ: 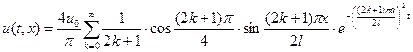 .
.
5. Найти решение смешанной задачи

Ответ:  .
.
6. Найти закон распределения температуры в стержне длиной π с теплоизолированной боковой поверхностью, если на концах стержня 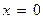 и
и  поддерживается нулевая температура, а начальная температура стержня задана функцией
поддерживается нулевая температура, а начальная температура стержня задана функцией 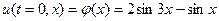 .
.
Ответ:  .
.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 11268; Нарушение авторских прав?; Мы поможем в написании вашей работы!