
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 1.Если сходится,то сходится и . 1 страница
|
|
|
|
► Пусть 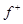 и
и 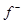 - неотрицательные составляющие функции f. Тог- да | f | =
- неотрицательные составляющие функции f. Тог- да | f | =  , и при всяком х, a< х <b, имеем
, и при всяком х, a< х <b, имеем  =
= 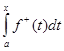 + +
+ + 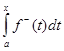 ; отсюда, так как
; отсюда, так как 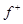 и
и 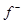 неотрицательны, вытекают неравенства
неотрицательны, вытекают неравенства 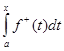 ≤
≤ 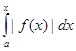 и
и 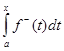 ≤
≤ 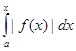 , справедливые при всяком х, a<х <b. Кроме того, при тех же х
, справедливые при всяком х, a<х <b. Кроме того, при тех же х 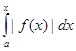 ≤
≤  . Таким образом, каж- дый из интегралов с переменным верхним пределом
. Таким образом, каж- дый из интегралов с переменным верхним пределом 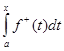 и
и 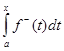 не убывает на [ a,b) и ограничен сверху числом
не убывает на [ a,b) и ограничен сверху числом  ; значит, существу- ют пределы
; значит, существу- ют пределы 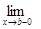
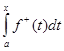 и
и 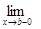
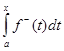 . Тогда существует и предел
. Тогда существует и предел 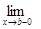
 =
= 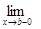
 , т.е. интеграл
, т.е. интеграл 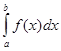 сходится.◄
сходится.◄
Определение 1. Функцию f назовём абсолютно интегрируемой на [ a,b), если интеграл  существует (т.е. является либо определен- ным интегралом, либо сходящимся несобственным).
существует (т.е. является либо определен- ным интегралом, либо сходящимся несобственным).
Теорема 2. (Признак Вейерштрасса) Пусть функции f и g интег- рируемы на всяком сегменте [ a,x ], где a<х <b. Если 1) при всех 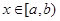 | f (x)| ≤ g (x) (следовательно, g неотрицательна на [ a,b)) и 2)
| f (x)| ≤ g (x) (следовательно, g неотрицательна на [ a,b)) и 2)  существует, то f абсолютно интегрируема на [ a,b).
существует, то f абсолютно интегрируема на [ a,b).
► Из 1) следует: при всех 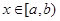
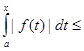
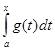 . Так как g не- отрицательна на [ a,b), то
. Так как g не- отрицательна на [ a,b), то 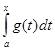 ≤
≤  . Следовательно, при всех
. Следовательно, при всех 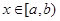
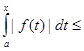
 , т.е. не убывающая на [ a,b) функция
, т.е. не убывающая на [ a,b) функция  ог- раничена сверху числом
ог- раничена сверху числом  . Значит, существует
. Значит, существует 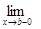
 , а это означает, что существует
, а это означает, что существует  ; поэтому f абсолютно интегрируема на [ a,b).◄
; поэтому f абсолютно интегрируема на [ a,b).◄
Пусть функция f определена на промежутке (a,b ], a<b, ограничен- ном или неограниченном и интегрируема на сегменте [ x,b ] при всяком х, a< х <b. Для такой функции 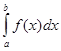 и
и  - либо определенные ин- тегралы (когда f интегрируема на ограниченном (a,b ], либо несобствен- ные, сходящиеся или расходящиеся (когда а – особая точка для f или a = -∞). Если
- либо определенные ин- тегралы (когда f интегрируема на ограниченном (a,b ], либо несобствен- ные, сходящиеся или расходящиеся (когда а – особая точка для f или a = -∞). Если  сходится, то сходится и
сходится, то сходится и 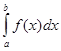 - доказательство этого утверждения аналогично доказательству теоремы 1.
- доказательство этого утверждения аналогично доказательству теоремы 1.
Определение 2. Функцию f назовём абсолютно интегрируемой на (a,b ], если интеграл  существует.
существует.
Теорема 3. (Признак Вейерштрасса) Пусть функции f и g интег- рируемы на всяком сегменте [ x,b ], где a< х <b. Если 1) при всех 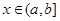 | f (x)| ≤ g (x) и 2)
| f (x)| ≤ g (x) и 2)  существует, то f абсолютно интегрируема на (a,b ]
существует, то f абсолютно интегрируема на (a,b ]
|
|
|
Доказательство здесь аналогично доказательству теоремы 2.
Пусть функция f определена на интервале (a,b), a<b, ограниченном или неограниченном и интегрируема на всяком сегменте, содержащемся в (a,b). Тогда интегралы 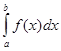 и
и  - либо определенные (когда (a,b) ограничен, а f интегрируема на нем), либо несобственные, сходящие- ся или расходящиеся (когда хотя бы один из концов a и b является особой точкой для f или интервал (a,b) неограничен). Напомним: несобственный интеграл
- либо определенные (когда (a,b) ограничен, а f интегрируема на нем), либо несобственные, сходящие- ся или расходящиеся (когда хотя бы один из концов a и b является особой точкой для f или интервал (a,b) неограничен). Напомним: несобственный интеграл 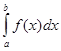 по (a,b) называют сходящимся, если существуют интег-ралы
по (a,b) называют сходящимся, если существуют интег-ралы 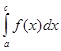 и
и  (т.е. либо оба они сходящиеся несобственные, ли- бо один из них определенный интеграл, а другой – сходящийся несобст -венный); здесь с – точка, произвольно выбранная на (a,b). Из изложенного выше ясно: если
(т.е. либо оба они сходящиеся несобственные, ли- бо один из них определенный интеграл, а другой – сходящийся несобст -венный); здесь с – точка, произвольно выбранная на (a,b). Из изложенного выше ясно: если  существует, то существует и
существует, то существует и 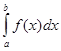 .
.
Определение 3. Функцию f назовём абсолютно интегрируемой на (a,b), если интеграл  существует.
существует.
Теорема 4 (Признак Вейерштрасса) Пусть функции f и g интегри- руемы на всяком сегменте, содержащемся в (a,b). Если 1) при всех 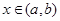 | f (x)| ≤ g (x) и 2)
| f (x)| ≤ g (x) и 2)  существует, то f абсолютно интегрируема на (a,b).
существует, то f абсолютно интегрируема на (a,b).
Это утверждение непосредственно вытекает из теорем 2 и 3.
Пусть 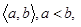 - произвольный промежуток, ограниченный или не- ограниченный, а функция f определена во всех точках этого промежутка, за возможным исключением нескольких точек xj, j= 0,1,2,…,l, где
- произвольный промежуток, ограниченный или не- ограниченный, а функция f определена во всех точках этого промежутка, за возможным исключением нескольких точек xj, j= 0,1,2,…,l, где 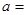
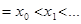 .
. 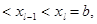 - в них f может быть определена, но не обязатель- но. Потребуем, чтобы f была интегрируема на любом сегменте, который лежит на
- в них f может быть определена, но не обязатель- но. Потребуем, чтобы f была интегрируема на любом сегменте, который лежит на  и не содержит ни одной из точек xj, j= 0,1,2,…,l. Тогда каждый из интегралов от функции f по интервалам (xj-1,xj), j = 1,2,…,l, является либо определенным интегралом, либо несобственным, сходящим- ся или расходящимся. Символом
и не содержит ни одной из точек xj, j= 0,1,2,…,l. Тогда каждый из интегралов от функции f по интервалам (xj-1,xj), j = 1,2,…,l, является либо определенным интегралом, либо несобственным, сходящим- ся или расходящимся. Символом 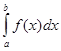 обозначим интеграл от функции f по промежутку
обозначим интеграл от функции f по промежутку  , определив это понятие как сумму интегралов по интервалам (xj-1,xj), j = 1,2,…,l:
, определив это понятие как сумму интегралов по интервалам (xj-1,xj), j = 1,2,…,l: 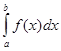
 . Интеграл
. Интеграл 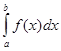 на- зовем определенным, если все слагаемые в этой сумме являются опреде- ленными интегралами. и несобственным, если хотя бы одно слагаемое представляет собой несобственный интеграл. Несобственный интеграл
на- зовем определенным, если все слагаемые в этой сумме являются опреде- ленными интегралами. и несобственным, если хотя бы одно слагаемое представляет собой несобственный интеграл. Несобственный интеграл 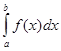 назовем сходящимся, если сходятся все несобственные интегралы, входящие в сумму
назовем сходящимся, если сходятся все несобственные интегралы, входящие в сумму  ; в противном случае, т.е. когда среди слага- емых имеется хотя бы один расходящийся интеграл, будем говорить, что
; в противном случае, т.е. когда среди слага- емых имеется хотя бы один расходящийся интеграл, будем говорить, что 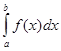 расходится. Будем говорить, что интеграл
расходится. Будем говорить, что интеграл 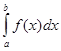 существует, ес- ли он являетя либо определенным, либо сходящимся несобственным ин -тегралом. Иными словами, интеграл
существует, ес- ли он являетя либо определенным, либо сходящимся несобственным ин -тегралом. Иными словами, интеграл 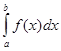 существует, если существуют все интегралы
существует, если существуют все интегралы  , j= 0,1,2,…,l, т.е. если каждый из них является либо определенным, либо сходящимся несобствнным интегралом. Ввиду изло- женного выше ясно: если существует
, j= 0,1,2,…,l, т.е. если каждый из них является либо определенным, либо сходящимся несобствнным интегралом. Ввиду изло- женного выше ясно: если существует  , то существует и
, то существует и 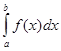 .
.
|
|
|
Определение 4. Функцию f, удовлетворяющую на  сформулиро- ванным выше условиям, назовем абсолютно интегрируемой на
сформулиро- ванным выше условиям, назовем абсолютно интегрируемой на  , если
, если  существует.
существует.
Отметим, что функция, абсолютно интегрируемая на промежутке [ a,b), (a,b ] или (a,b) (см. определения 1,2,3), удовлетворяет и определе- нию 4; в этих трех случаях можно считать, что набор 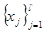 состоит из двух точек а и b.
состоит из двух точек а и b.
Теорема 5 (Признак Вейерштрасса) Пусть функции f и g удов- летворяют на  сформулированным выше условиям. Если 1) при всех
сформулированным выше условиям. Если 1) при всех  (xj-1,xj), j = 1,2,…,l, | f (x)| ≤ g (x) и 2)
(xj-1,xj), j = 1,2,…,l, | f (x)| ≤ g (x) и 2)  существует, то f абсо- лютно интегрируема на
существует, то f абсо- лютно интегрируема на  .
.
Это утверждение является следствием теорем 2,3,4.
п.2. Тригонометрический многочлен. Тригонометрический ряд
Пусть n – натуральное число, а 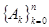 и
и 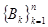 - заданные веществен- ные числа. Обозначим:
- заданные веществен- ные числа. Обозначим: 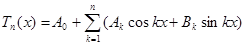 .
. 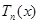 называют тригонометрическим многочленом порядка не выше n, числа
называют тригонометрическим многочленом порядка не выше n, числа 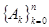 и
и 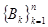 - его коэффициентами,
- его коэффициентами, 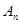 и
и  - его старшими коэффициентами. Если хотя бы один из старших коэффициентов отличен от нуля,
- его старшими коэффициентами. Если хотя бы один из старших коэффициентов отличен от нуля, 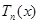 называют тригонометрическим многочленом порядка n. Очевидно,
называют тригонометрическим многочленом порядка n. Очевидно, 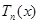 есть 2π – периодическая функция, непрерывная на всей числовой оси. Приведем формулировку одной из важнейших теорем математического анализа.
есть 2π – периодическая функция, непрерывная на всей числовой оси. Приведем формулировку одной из важнейших теорем математического анализа. 
Теорема 1. (Теорема Вейерштрасса о приближении непрерывной функции тригонометрическими многочленами) Пусть функция f непре- рывна на сегменте [-π,π], причем f (-π )= f (π). Тогда существует последо- вательность  тригонометрических многочленов, равномерно сходя- щаяся на [-π,π] к функции f, т.е.
тригонометрических многочленов, равномерно сходя- щаяся на [-π,π] к функции f, т.е.
|
|
|
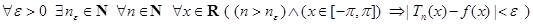
Доказательство этой теоремы можно найти в руководствах по мате- матическому анализу.
Пусть заданы две последовательности вещественных чисел 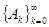 и
и 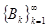 . Функциональный ряд
. Функциональный ряд 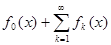 , где
, где 
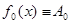 , а при всяком натуральном
, а при всяком натуральном 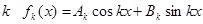 , называют тригонометрическим рядом. Его n- ая частичная сумма
, называют тригонометрическим рядом. Его n- ая частичная сумма 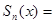

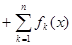 представляет собой тригонометрический многочлен порядка не выше n. Если тригонометриче- ский ряд сходится на некотором промежутке
представляет собой тригонометрический многочлен порядка не выше n. Если тригонометриче- ский ряд сходится на некотором промежутке  , то он сходится на вся- ком промежутке вида
, то он сходится на вся- ком промежутке вида 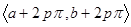 , где р – целое число. Если он сходит ся на сегменте [-π,π], то он сходится на всей числовой оси, а его сумма
, где р – целое число. Если он сходит ся на сегменте [-π,π], то он сходится на всей числовой оси, а его сумма  есть 2π – периодическая функция. Если ряд равномерно сходится на [-π,π], то
есть 2π – периодическая функция. Если ряд равномерно сходится на [-π,π], то  - непрерывная 2π – периодическая функция.
- непрерывная 2π – периодическая функция.
Лемма. При любых целых p и q

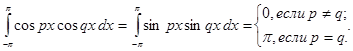
Для доказательства этих равенств нужно преобразовать подынтег- ральные произведения в суммы.
Теорема 2. ( О коэффициентах равномерно сходящегося тригоно-метрического ряда ) Пусть тригонометрический ряд
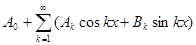 равномерно сходится на [-π,π], а
равномерно сходится на [-π,π], а  - его сумма. Тогда
- его сумма. Тогда
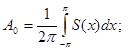 при
при 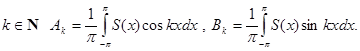
► На сегменте [-π,π] справедливо
 (1) Проинтегрируем это равенство. Так как равномерно сходящийся ряд можно интегрировать почленно, получим:
(1) Проинтегрируем это равенство. Так как равномерно сходящийся ряд можно интегрировать почленно, получим:
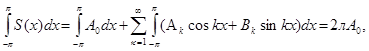 Отсюда:
Отсюда: 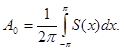 Пусть р – заданное натуральное число. Умножим (1) на cospx и проинтегрируем полученное равенство. Учитывая равенства леммы, получим:
Пусть р – заданное натуральное число. Умножим (1) на cospx и проинтегрируем полученное равенство. Учитывая равенства леммы, получим:
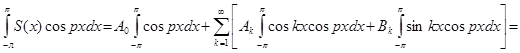
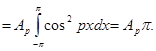
Отсюда: 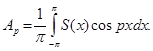 Аналогично, умножив (1) на sinpx, до- кажем равенство
Аналогично, умножив (1) на sinpx, до- кажем равенство 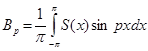 . ◄
. ◄
п.3. Коэффициенты Фурье и ряд Фурье функции, абсолютно
интегрируемой на 
Пусть функция f определена во всех точках сегмента  , за исключением, быть может, точек xj, j= 0,1,2,…,l,
, за исключением, быть может, точек xj, j= 0,1,2,…,l, 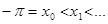
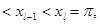 (они могут быть особыми точками для функции f) и абсолютно интегри- руема на
(они могут быть особыми точками для функции f) и абсолютно интегри- руема на  . Заметим,что при любом натуральном k существуют ин-
. Заметим,что при любом натуральном k существуют ин-  тегралы
тегралы 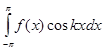 и
и 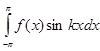 . Действительно, при всех
. Действительно, при всех 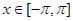 имеем | f(x) coskx | ≤ g(x), где g(x) = | f(x) |, причем
имеем | f(x) coskx | ≤ g(x), где g(x) = | f(x) |, причем  существует, так как f абсолютно интегрируема на
существует, так как f абсолютно интегрируема на  . В силу признака Вейерштрасса f(x) coskx абсолютно интегрируема на
. В силу признака Вейерштрасса f(x) coskx абсолютно интегрируема на  ; значит,
; значит, 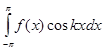 суще- ствует. Существование
суще- ствует. Существование 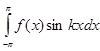 устанавливается аналогично.
устанавливается аналогично.
Введем обозначения:
 при
при  . Числа
. Числа 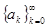 и
и  называют коэффициентами Фурье функции f; триго- нометрический ряд
называют коэффициентами Фурье функции f; триго- нометрический ряд 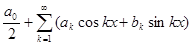 называют рядом Фурье этой функции.
называют рядом Фурье этой функции.
|
|
|
Замечание. Если тригонометрический ряд  равномерно сходится на
равномерно сходится на  , а S(x) – его сумма, то коэффициенты ряда являются коэффициентами Фурье функции S(x) (см. теорему 2, п.2).
, а S(x) – его сумма, то коэффициенты ряда являются коэффициентами Фурье функции S(x) (см. теорему 2, п.2).
Пусть ряд Фурье функции f сходится на некотором множестве Х 
 . Тогда на Х определена функция S(x) – сумма ряда Фурье и, значит, на этом множестве определены две функции - f(х) и S(x). Вообще говоря, они различны между собой. Если же на множестве Х f(х) и S(x) совпада- ют, то говорят что функция f разлагается на множестве Х в ряд Фурье и при этом записывают: f(х) =
. Тогда на Х определена функция S(x) – сумма ряда Фурье и, значит, на этом множестве определены две функции - f(х) и S(x). Вообще говоря, они различны между собой. Если же на множестве Х f(х) и S(x) совпада- ют, то говорят что функция f разлагается на множестве Х в ряд Фурье и при этом записывают: f(х) = 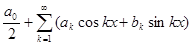 на множестве Х.
на множестве Х.
Приведем формулировки основных теорем о разложении функции в ряд Фурье. Сначала введем в употребление следующие определения.
Пусть 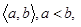 - ограниченный промежуток, а
- ограниченный промежуток, а  ,
, 
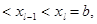 - набор некоторых точек. Сформулированные ниже определе- ния касаются функций, которые определены во всех точках этого проме- жутка, за возможным исключением точек xj, j= 0,1,2,…,l, - в них рассмат- риваемые функции могут быть определены, но не обязательно.
- набор некоторых точек. Сформулированные ниже определе- ния касаются функций, которые определены во всех точках этого проме- жутка, за возможным исключением точек xj, j= 0,1,2,…,l, - в них рассмат- риваемые функции могут быть определены, но не обязательно.
Определение 1. Будем говорить, что функция f кусочно-монотонна на 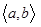 , если f монотонна (т.е. либо не убывает, либо не возрастает) на каждом из интервалов Xj = (xj-1, xj), j= 1,2,…,l.
, если f монотонна (т.е. либо не убывает, либо не возрастает) на каждом из интервалов Xj = (xj-1, xj), j= 1,2,…,l.
Определение 2. Будем говорить, что функция f кусочно- непрерывна на 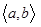 , если
, если
f непрерывна на каждом из интервалов Xj = (xj-1, xj), j= 1,2,…,l;
в каждой из внутренних точек xj, j= 1,2,…,l-1, cуществуют односторонние пределы f (x j - 0) и f (x j+0);
существуют f (a j+0) и f (b j - 0).
Заметим, что в точках xj, j= 0,1,2,…,l кусочно – непрерывная функ- ция может быть не определена; если же она определена в точке xj, то её значение f (xj) может не совпадать с её односторонними пределами в этой точке. Кусочно- непрерывная на 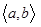 функция ограничена на
функция ограничена на 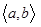 и либо непрерывна на этом промежутке, либо имеет на нем конечное количество точек разрыва первого рода. Отсюда вытекает, что f интегрируема, а пото- му и абсолютно интегрируема на
и либо непрерывна на этом промежутке, либо имеет на нем конечное количество точек разрыва первого рода. Отсюда вытекает, что f интегрируема, а пото- му и абсолютно интегрируема на 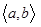 .
.
Определение 3. Функцию f назовём кусочно-гладкой на промежут- ке 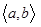 , если она имеет на этом промежутке кусочно- непрерывную про -изводную.
, если она имеет на этом промежутке кусочно- непрерывную про -изводную.
Теорема 1. ( Теорема Дирихле ) Пусть функция f кусочно- монотонна и кусочно- непрерывна на сегменте  . Тогда её ряд Фурье сходится в каждой точке этого сегмента, а для его суммы S(x) справедливы утвержде- ния:
. Тогда её ряд Фурье сходится в каждой точке этого сегмента, а для его суммы S(x) справедливы утвержде- ния:
при всяком 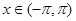 S(x) =
S(x) = 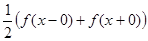 ;
;
S(-π) = S(π) =  .
.
Замечание. Во всякой точке интервала 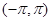 , в которой f непрерыв- на, имеет место равенство f(х) = S(x).
, в которой f непрерыв- на, имеет место равенство f(х) = S(x).
Следствие. Если функция f кусочно –монотонна и непрерывна на  и удовлетворяет условию f(-π) = f(π), то она разлагается на этом сегменте в ряд Фурье.
и удовлетворяет условию f(-π) = f(π), то она разлагается на этом сегменте в ряд Фурье.
Теорема 2. Пусть функция f 1) абсолютно интегрируема на сегмен- те  , 2) в каждой точке интервала
, 2) в каждой точке интервала 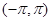 существуют односторонние производные
существуют односторонние производные 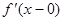 и
и 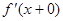 , 3) существуют односторонние производ- ные
, 3) существуют односторонние производ- ные  и
и  . Тогда ряд Фурье этой функции сходится на
. Тогда ряд Фурье этой функции сходится на  , а для его суммы S(x) справедливы утверждения:
, а для его суммы S(x) справедливы утверждения:
1) если 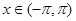 , то S(x) =
, то S(x) = 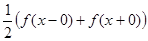 ;
;
S(-π) = S(π) = 
Замечание. Утверждения 1) и 2) справедливы, если функция f явля- ется кусочно- гладкой на  .
.
Теорема 3. Функция f, непрерывная и кусочно- гладкая на сегмен- те  и удовлетворяющая условиям f(-π) = f(π),
и удовлетворяющая условиям f(-π) = f(π), 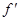 (-π) =
(-π) = 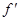 (π) разлагает- ся на этом сегменте в ряд Фурье, равномерно сходящийся на
(π) разлагает- ся на этом сегменте в ряд Фурье, равномерно сходящийся на  .
.
Ввиду грамоздкости доказательств этих теорем мы их здесь не при- водим; их можно найти в руководствах по математическому анализу.
п.4. Почленное дифференцирование и интегрирование ряда Фурье
Пусть функция f и её производная 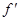 абсолютно интегрируемы на
абсолютно интегрируемы на  и, кроме того, f(-π) = f(π). Запишем ряды Фурье этих функций:
и, кроме того, f(-π) = f(π). Запишем ряды Фурье этих функций:
f(х) 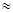
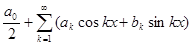 ;
; 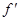 (х)
(х) 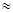
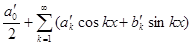 . Здесь символ
. Здесь символ 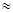 означает, что тригонометрический ряд представляет собой ряд Фурье соответствующей функции; при этом не предполагается, что функция разлагается в этот ряд, не предполагается даже, что этот ряд сходится. Запишем выражения для коэффициентов Фурье производной
означает, что тригонометрический ряд представляет собой ряд Фурье соответствующей функции; при этом не предполагается, что функция разлагается в этот ряд, не предполагается даже, что этот ряд сходится. Запишем выражения для коэффициентов Фурье производной 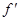 :
:
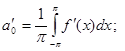 при
при 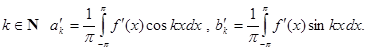 . Пусть функция
. Пусть функция 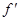 такова, что к этим интегралам применима формула ин- тегрирования по частям (например,
такова, что к этим интегралам применима формула ин- тегрирования по частям (например, 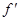 непрерывна на
непрерывна на  .). Тогда, учи- тывая равенство f(-π) = f(π), получим:
.). Тогда, учи- тывая равенство f(-π) = f(π), получим:
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 431; Нарушение авторских прав?; Мы поможем в написании вашей работы!